Help me! (Lớp 11)
giải phương trình sau:
sin3x - cos5x = 0
PA
Những câu hỏi liên quan
Giải phương trình: cos5x + x2 0 A. B. C. D.Vô nghiệm
Đọc tiếp
Giải phương trình: cos5x + x2 = 0
A. 
B. 
C. 
D.Vô nghiệm
Giải phương trình sau: sin3x - cos5x = 0
sin3x - cos5x = 0
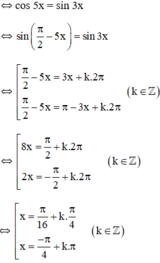
Vậy phương trình có hai họ nghiệm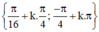 
(k ∈ Z).
Đúng 0
Bình luận (0)
Giải các phương trình sau:
1) \(2\cos4x-3=0\)
2) \(cos5x+2=0\)
3) \(cos2x+0,7=0\)
4) \(cos^22x-\dfrac{1}{4}=0\)
1.
\(2cos4x-3=0\)
\(\Leftrightarrow cos4x=\dfrac{3}{2}\)
Mà \(cos4x\in\left[-1;1\right]\)
\(\Rightarrow\) phương trình vô nghiệm.
2.
\(cos5x+2=0\)
\(\Leftrightarrow cos5x=-2\)
Mà \(cos5x\in\left[-1;1\right]\)
\(\Rightarrow\) phương trình vô nghiệm.
Đúng 1
Bình luận (0)
3.
\(cos2x+0,7=0\)
\(\Leftrightarrow cos2x=-\dfrac{7}{10}\)
\(\Leftrightarrow2x=\pm arccos\left(-\dfrac{7}{10}\right)+k2\pi\)
\(\Leftrightarrow x=\pm\dfrac{arccos\left(-\dfrac{7}{10}\right)}{2}+k\pi\)
4.
\(cos^22x-\dfrac{1}{4}=0\)
\(\Leftrightarrow cos^22x=\dfrac{1}{4}\)
\(\Leftrightarrow\left[{}\begin{matrix}cos2x=-\dfrac{1}{2}\\cos2x=\dfrac{1}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}2x=\pm\dfrac{2\pi}{3}+k2\pi\\2x=\pm\dfrac{\pi}{3}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\pm\dfrac{\pi}{3}+k\pi\\x=\pm\dfrac{\pi}{6}+k\pi\end{matrix}\right.\)
Đúng 1
Bình luận (0)
Giải phương trình
sin
3
x
+
cos
3
x
2
sin
5
x
+
cos
5
x
Đọc tiếp
Giải phương trình sin 3 x + cos 3 x = 2 sin 5 x + cos 5 x
Giải phương trình
sin
3
x
+
cos
3
x
2
sin
5
x
+
cos
5
x
. A.
x
-
π
4
+
k
2...
Đọc tiếp
Giải phương trình sin 3 x + cos 3 x = 2 sin 5 x + cos 5 x .
A. x = - π 4 + k 2 π
B. x = π 4 + k π .
C. x = π 4 + k π 2
D. x = π 4 + k 2 π
Giải phương trình sau: cos3x - cos5x = sinx
cos3x – cos5x = sinx ⇔ sinx(1 – 2sin4x) = 0
Đúng 0
Bình luận (0)
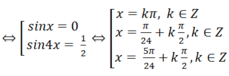
Giải các phương trình sau sin5x + cos5x = -1
giải pt: cos3x + cos5x + cos8x +1 =0
help pls :(
\(\Leftrightarrow2cos4x.cosx+2cos^24x-1+1=0\)
\(\Leftrightarrow2cos4x\left(cos4x+cosx\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cos4x=0\\cos4x+cosx=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}cos4x=0\\cos4x=cos\left(\pi-x\right)\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}4x=\frac{\pi}{2}+k\pi\\4x=\pi-x+k2\pi\\4x=x-\pi+k2\pi\end{matrix}\right.\) \(\Leftrightarrow x=...\)
Đúng 0
Bình luận (0)
MM
28 tháng 9 2021 lúc 20:50
Giải các phương trình:
\(a,sinx-cosx=1\)
\(b,cos3x.cos2x=cos5x\)
a, \(sinx-cosx=1\)
\(\Leftrightarrow\sqrt{2}sin\left(x-\dfrac{\pi}{4}\right)=1\)
\(\Leftrightarrow sin\left(x-\dfrac{\pi}{4}\right)=\dfrac{1}{\sqrt{2}}\)
\(\Leftrightarrow\left[{}\begin{matrix}x-\dfrac{\pi}{4}=\dfrac{\pi}{4}+k2\pi\\x-\dfrac{\pi}{4}=\dfrac{3\pi}{4}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{2}+k2\pi\\x=\pi+k2\pi\end{matrix}\right.\)
Đúng 2
Bình luận (0)
b, \(cos3x.cos2x=cos5x\)
\(\Leftrightarrow\dfrac{1}{2}cos5x+\dfrac{1}{2}cosx=cos5x\)
\(\Leftrightarrow cosx=cos5x\)
\(\Leftrightarrow5x=\pm x+k2\pi\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{k\pi}{2}\\x=\dfrac{k\pi}{3}\end{matrix}\right.\)
Đúng 1
Bình luận (0)