Định m để hàm số xác định với mọi x dương: a) y = √x - m - 1 + √4x - m.
NV
Những câu hỏi liên quan
Tìm m để hàm số \(y=\sqrt{\dfrac{sin2x-cos2x+m-1}{6\left(cos^4x+sin^4x\right)+cos8x+7-5m}}\) xác định với mọi số thực x
\(y=\sqrt{\dfrac{\sqrt{2}sin\left(2x-\dfrac{\pi}{4}\right)+m-1}{2cos^24x+\dfrac{3}{2}cos4x+\dfrac{21}{2}-5m}}\)
Hàm xác định trên R khi:
TH1: \(\left\{{}\begin{matrix}\sqrt{2}sin\left(2x-\dfrac{\pi}{4}\right)+m-1\ge0\\2cos^24x+\dfrac{3}{2}cos4x+\dfrac{21}{2}-5m>0\end{matrix}\right.\) ;\(\forall x\)
\(\Rightarrow\left\{{}\begin{matrix}-m\le\min\limits_R\left(\sqrt{2}sin\left(2x-\dfrac{\pi}{4}\right)-1\right)=-1-\sqrt{2}\\5m< \min\limits_R\left(2cos^24x+\dfrac{3}{2}cos4x+\dfrac{21}{2}\right)=\dfrac{327}{32}\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}m\ge1+\sqrt{2}\\m< \dfrac{327}{160}\end{matrix}\right.\) \(\Rightarrow m\in\varnothing\)
Th2: \(\left\{{}\begin{matrix}\sqrt{2}sin\left(2x-\dfrac{\pi}{4}\right)+m-1\le0\\2cos^24x+\dfrac{3}{2}cos4x+\dfrac{21}{2}-5m< 0\end{matrix}\right.\) ;\(\forall x\)
\(\Rightarrow\left\{{}\begin{matrix}m\le\min\limits_R\left(\sqrt{2}sin\left(2x-\dfrac{\pi}{4}\right)-1\right)=-1-\sqrt{2}\\5m>\max\limits_R\left(2cos^24x+\dfrac{3}{2}cos4x+\dfrac{21}{2}\right)=14\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}m\le-1-\sqrt{2}\\m>\dfrac{14}{5}\end{matrix}\right.\) \(\Rightarrow m\in\varnothing\)
Đúng 1
Bình luận (1)
Cho hàm số y = (3 – m)x2a) Tìm điều kiện của m để hàm số trên được xác định.b) Xác định m để hàm số đồng biến với mọi x < 0.c) Xác định m để y = 0 là giá trị nhỏ nhất của hàm số tại x = 0.
a, ĐKXĐ để hàm được xác định : \(3-m\ne0\)
\(\Leftrightarrow m\ne3\)
b, - Với x < 0 để hàm số đồng biến thì : \(3-m< 0\)
\(\Leftrightarrow m>3\)
Vậy ...
c, - Để y = 0 là giá trị nhỏ nhất của hàm số tại x = 0
\(\Leftrightarrow a>0\)
\(\Leftrightarrow3-m>0\)
\(\Leftrightarrow m< 3\)
Vậy ...
Đúng 2
Bình luận (0)
a) Để hàm số \(y=\left(3-m\right)x^2\) được xác định thì \(3-m\ne0\)
hay \(m\ne3\)
b) Để hàm số \(y=\left(3-m\right)x^2\) đồng biến với mọi x<0 thì \(3-m< 0\)
\(\Leftrightarrow m>3\)
c) Để y=0 là giá trị nhỏ nhất của hàm số tại x=0 thì 3-m>0
hay m<3
Đúng 2
Bình luận (0)
Tính m để hàm số xác định với mọi x lớn hơn 0
\(y=\sqrt{x-m-1}+\sqrt{4x-m}\)
1.Tìm tập xác định của hàm số: y= \(\sqrt{1+sinx-2cos^2x}\)
2. Cho hàm số: y = \(\sqrt{sin^4x+cos^4x-2msinx.cosx}\)
Tìm các giá trị của m để xác định với mọi x.
Xác định m để hàm số \(y=\sqrt{(m+1)x^2-2(m-1)x+3m-3} \) có nghĩa với mọi x
Với \(m=-1\) ktm
Với \(m\ne-1\)
\(\Leftrightarrow\left\{{}\begin{matrix}m+1>0\\\Delta'=\left(m-1\right)^2-\left(m+1\right)\left(3m-3\right)\le0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m>-1\\\left(m-1\right)\left(-2m-4\right)\le0\end{matrix}\right.\)
\(\Leftrightarrow m>1\)
Đúng 0
Bình luận (0)
Giá trị của m để hàm số `y=\sqrt{x-m}+\sqrt{2x-m+1}` xác định với mọi `x>0`
Cho hàm số bậc nhất: y = (m – 1)x + 3 (1) (với m ≠ 1) a) Xác định m để hàm số (1) đồng biến trên R b) Xác định m, biết đồ thị của hàm số (1) song song với đường thẳng y = – x + 1 c) Xác định m để đường thẳng (d1): y = 1 – 3x; (d2): y = – 0,5x – 1,5 và đồ thị của hàm số (1) cùng đi qua một điểm.
Đây nhé bn !
Cho hàm số y=(m+1)x-1
a/ xác định m để hàm số đã cho đi qua trung điểm (1; 0)
b/ xác định m để hàm số đã cho song song với đường thẳng y=x+3
hs y=(m+1)x-1 là hs bậc nhất khi và chỉ khi : m+1 khác 0 suy ra m khác -1.
a) hs y=(m+1)x-1 đi qua điểm (1;0) nên thay x=1 ; y=0 vào hs trên ta được (m+1)1-1=0 suy ra m=0.
b) đường thẳng y=(m+1)x-1 song song với đường thẳng y=x+3 khi và chỉ khi :
m+1=1 suy ra m=0.
Đúng 0
Bình luận (0)
Tìm m để hàm số
y
5
sin
4
x
-
6
cos
4
x
+
2
m
-
1
xác định với mọi x
Đọc tiếp
Tìm m để hàm số y = 5 sin 4 x - 6 cos 4 x + 2 m - 1 xác định với mọi x
![]()
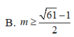
![]()
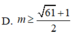
Hàm số xác định với mọi x khi và chỉ khi 5sin4x – 6cos4x + 2m- 1 ≥ 0 ∀ x
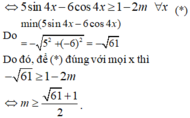
Đáp án D
Đúng 0
Bình luận (0)





