Tìm ab biết:ab2=ab+230
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
VA
Những câu hỏi liên quan
ngày 30 tháng 7 là cung gì mấy bn ?
ab5 - ab = 230
tìm giá trị của a và b
trả lời cả 2 câu nhé các bn
Ngày 30 tháng 7 là cung Sư Tử.
Ab5- ab=230
5-b=0.=>b=5
b=5 thì b-a=5-a=3.=>a=2
Vậy a=2 và b=5
Đúng 0
Bình luận (0)
Ngày 30/7 là cung sư tử .
ab5 - ab = 230
5 - b = 0 . suy ra b = 5 .
b = 5 thì b - a = 5 - a = 3 . suy ra : a = 2 .
Vậy a = 2 và b = 5
Đúng 0
Bình luận (0)
Một thửa vườn hình tam giác vuông ABC vuông ở A. cạnh AC lớn hơn cạnh AB 30m. Cạnh BC dài 150m.
a). Tính độ dài cạnh AB và AC.Biết chu vi thửa vườn là 360m.
b). Tính diện tích thửa vườn đó.
c). Ở giữa vườn người ta đào một ao cá hình vuông chu vi 100m. Tính diện tích còn lại để trồng trọt.
Tổng 2 canh góc vuông là : 360-150= 210(m)
Cạnh AC (210+30):2= 120m
Cạnh AB: 120-30= 90m
S= (90x120):2= 5400 m2
P= 100m => r= 100: (2x3,14)= 15,92m S ao: 15,92x15,92x3,14= 795,82 m2 S còn lại 5400- 795,82= 4604,18 m2
Đúng 0
Bình luận (0)
Tổng 2 canh góc vuông là : 360-150= 210(m)
Cạnh AC (210+30):2= 120m
Cạnh AB: 120-30= 90m
S= (90x120):2= 5400 m2
P= 100m => r= 100: (2x3,14)= 15,92m S ao: 15,92x15,92x3,14= 795,82 m2 S còn lại 5400- 795,82= 4604,18 m2
Đúng 0
Bình luận (0)
Hạt nhân urani \(U^{234}_{92}\) phóng xạ cho hạt nhân con thori \(Th^{230}_{90}\) thì đó là sự phóng xạ
A. a
B. \(\beta^-\)
C. \(\beta^1\)
D. \(\gamma\)
Hạt nhân urani \(U_{92}^{234}\) phóng xạ cho hạt nhân con thori \(Th_{90}^{230}\) thì đó là sự phóng xạ
\(A.\alpha\)
Đúng 1
Bình luận (0)
Bài 1 : Trên cùng tia ox lấy hai điểm A và B sao cho điểm A nằm giữa o và B. Biết oA = 5 cm, oB = 7cm.Tính đọ dài đoạn thẳng AB.
Bài 2 : Vẽ hai tia ox, oy đối nhau. Lấy A thuộc ox và B thuộc oy sao cho oA bằng 7cm, oB bằng 5cm .Tính AB.
Bài 3: Tìm số tự nhiên A biết 404 chia A dư 8 và 230 chia A dư 14
Hai tiếp tuyến tại a và b của đường tròn cắt nhau tại S biết góc asb = 50° thì số đo của cung nhỏ AB bằng:a.130° b.310° c.50° d.230°
Bính đi từ A đến B. Nửa quãng đường đầu Bính đi với vận tốc 60 km/giờ. Nửa quãng đường còn lại Bính đi với vận tốc 30 km/giờ.Tính vận tốc trung bình của Bính trên suốt quãng đường AB. Trả lời: Vận tốc trung bình của Bính trên suốt quãng đường AB là 230 km/giờ.
Hai đường thẳng AB và CD cắt nhau tại O tạo thành bốn góc khác góc bẹt( trong đó AOC < BOC). Tính số đo 4 góc ấy, biết rằng ba góc có tổng số đo bằng 230 độ
Hai đường thẳng AB và CD cắt nhau tại O tạo thành bốn góc khác góc bẹt ( trong đó góc AOC < góc BOC ). Tính số đo của bốn góc đó, biết rằng có ba góc có tổng số đo bằng 230 độ.
TH1: \(\widehat{AOC}+\widehat{AOD}+\widehat{BOD}=230o\)
Mà \(\widehat{AOC}=\widehat{BOD}\) (2 góc đối đỉnh)
=> \(2.\widehat{AOC}+\widehat{AOD}=230o\)
Mà \(\widehat{AOC}+\widehat{AOD}=180o\) (2 góc kề bù)
=> \(\left\{{}\begin{matrix}\widehat{AOC}=\widehat{BOD}=50o\\\widehat{AOD}=\widehat{BOC}=130o\end{matrix}\right.\)
TH2: \(\widehat{AOD}+\widehat{BOD}+\widehat{BOC}=230o\)
Mà \(\widehat{AOD}=\widehat{BOC}\) (2 góc đối đỉnh)
=> \(2.\widehat{AOD}+\widehat{BOD}=230o\)
Mà \(\widehat{AOD}+\widehat{BOD}=180o\)
=> \(\left\{{}\begin{matrix}\widehat{AOD}=\widehat{BOC}=50o\\\widehat{BOD}=\widehat{AOC}=130o\end{matrix}\right.\)
vô lí do \(\widehat{AOC}>\widehat{BOC}\)
Đúng 1
Bình luận (0)
Cho tam giác ABC. Từ điểm D trên cạnh BC, kẻ các đường thẳng song song với các cạnh AB và AC, chúng cắt các cạnh AC và AB theo thứ tự tại F và E (h.4)
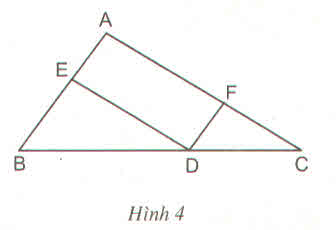
Chứng minh rằng :
\(\dfrac{AE}{AB}+\dfrac{AF}{AC}=1\)
Trong ∆ ABC ta có: DE // AC (gt)
Suy ra: \(\frac{AE}{AB}=\frac{CD}{CB}\)(định lí Ta-lét) (1)
Lại có: DF // AB (gt)
Suy ra: \(\frac{AF}{AC}=\frac{BD}{BC}\)(định lí Ta-lét) (2)
Cộng trừ vế (1) và (2), ta có:
\(\frac{AE}{AB}+\frac{AF}{AC}=\frac{CD}{BC}+\frac{BD}{BC}=\frac{BC}{BC}=1\)