cho tam giác ABC cân tại A, đường cao AD. Biết AB=10 cm; BC= 12 cm
a/tính độ đài đoạn thẳng BD, AD
b/ gọi G là trọng tâm của tam giác ABC. Chứng minh ba điểm A,G,D thẳng hàng
c/ chứng minh tam giác ABG = tam giác ACG
Bài 3 : Cho tam giác ABC cân tại A , đường cao AD . Biết AB = 10 cm ; BC = 12 cm .
a. Tính độ dài các đoạn thẳng BD , AD .
b. Gọi G là trọng tâm của tam giác ABC . Chứng minh rằng ba điểm A , G , D thẳng hàng .
c. Chứng minh tam giác ABG = tam giác ACG
a) BD=BC/2=12/2=6
Vậy BC=6cm
Áp dụng định lý Py ta go vào tam giác vuông ABD, ta có:
\(AB^2+BD^2=AD^2\)
\(10^2+6^2=136\)
=> AD=\(\sqrt{136}\)
b) Tam giác ABC cân tại A, đường cao AD
=> AD là đường phân giác góc BAC (1)
Sau đó cm góc BG là tia pg góc HBD và CG là tia pg góc DCL cắt nhu tại G.
=> AG là pg góc BAC (2)
Từ (1) và (2) => AG và AD trùng nhau.
=>A, G, D thẳng hàng
bài 1: Tính cạnh đáy BC của tam giác cân ABC biết đường cao ứng với cạnh đáy bằng 15,6 cm và đường cao ứng với cạnh bên bằng 12 cm
bài 2: Cho tam giác ABC vuông tại A , đường phân giác AD, đường cao AH.Biết BD = 7,5 cm và CD = 10 cm . Tính HA,HB,HD
Cho tam giác ABC cân tại A . Đường cao AH . Kẻ HD vuông góc với AB , HE vuông góc với AC a, cm AD =AE b, cm tam giác BDH=tam giác CEH
a) trong tam giác cân đường cao đồng thời là đường phân giác nên AH cũng là đường phân giác nên góc BAH = góc CAH
Xét ΔADH và ΔAEH có:
góc ADH=góc AEH (= 90o)
chung AH
góc HAD = góc HAE (cmt)
⇒ΔADH = ΔAEH(ch-gn)
⇒ DH = EH (2 cạnh tương ứng)
b) trong tam giác cân đường cao đồng thời là đường trung tuyến nên AH cũng là đường trung tuyến nên HB = HC
Xét ΔBDH và ΔCEH có:
góc BDH = góc CEH (=90o)
HB=HC(cmt)
góc B = góc C (ΔABC cân tại A)
⇒ ΔBDH = ΔCEH(ch-gn)
Hình vẽ: Bạn tự vẽ hình nhé !
a, Ta có:
△ABC cân tại A nên ∠ABC= ∠ACB hay ∠ABH= ∠ACH
và AB= AC
Xét △AHB và △AHC, có:
AB= AC ( theo chứng minh trên )
∠ABH= ∠ACH ( theo chứng minh trên )
AH: cạnh chung
Nên: △AHB= △AHC ( c.g.c)
⇒ ∠BAH= ∠CAH ( 2 góc tương ứng ) hay ∠DAH= ∠EAD
Xét △ADH và △AEH, có:
∠HDA= ∠HEA=90o ( Do HD ⊥ AB, HE ⊥ AC )
AH: cạnh chung
∠DAH= ∠EAH ( theo chứng minh trên )
Nên: △ADH= △AEH ( cạnh huyền- góc nhọn )
⇒ AD= AE ( 2 cạnh tương ứng ) ( đcpcm )
b,
Ta có: Do △ADH= △AEH nên :HD= HE ( 2 cạnh tương ứng )
AB= AC
⇒ AD+ DB= AE+EC
mà AD= AE nên DB= EC
Xét △BDH và △CEH, có:
∠BDH= ∠CEH=90o
HD= HE ( theo chứng minh trên )
DB= EC ( theo chứng minh trên )
Nên △BDH= △CEH ( c.g.c ) ( đcpcm)
a) Xét ΔABH vuông tại H và ΔACH vuông tại H có
AB=AC(ΔABC cân tại A)
AH chung
Do đó: ΔABH=ΔACH(Cạnh huyền-cạnh góc vuông)
Suy ra: \(\widehat{BAH}=\widehat{CAH}\)(hai góc tương ứng)
hay \(\widehat{DAH}=\widehat{EAH}\)
Xét ΔDAH vuông tại D và ΔEAH vuông tại E có
AH chung
\(\widehat{DAH}=\widehat{EAH}\)(cmt)
Do đó: ΔDAH=ΔEAH(Cạnh huyền-góc nhọn)
Suy ra: AD=AE(Hai cạnh tương ứng)
b) Xét ΔDBH vuông tại D và ΔECH vuông tại E có
HB=HC(ΔABH=ΔACH)
HD=HE(ΔDAH=ΔEAH)
Do đó: ΔDBH=ΔECH(cạnh huyền-cạnh góc vuông)
Cho tam giác ABC cân tại A các đường cao BD và CE cắt nhau tại H Chứng minh AD = AE cho AB = 10 cm AD = 6 cm Tính khoảng cách từ điểm B đến cạnh AC biết Bac = 50 độ tính BC Gọi M là trung điểm của BC Chứng minh ba điểm A M N thẳng hàng.
a: Xét ΔABD vuông tại D và ΔACE vuông tại E có
AB=AC
góc BAD chung
Do đó: ΔABD=ΔACE
Suy ra: AD=AE
b: \(BD=\sqrt{10^2-6^2}=8\left(cm\right)\)
d: Xét ΔHBC có \(\widehat{HBC}=\widehat{HCB}\)
nên ΔHBC cân tại H
=>HB=HC
hay H nằm trên đường trung trực của BC(1)
Ta có: ΔABC cân tại A
mà AM là đường trung tuyến
nên AM là đường trung trực của BC(2)
Từ (1) và (2) suy ra A,H,M thẳng hàng
Cho tam giác ABC cân tại A có AD là đường phân giác.
a) Chứng minh ∆ A B D = ∆ A C D .
b) Gọi G là trọng tâm của tam giác ABC. Chứng mình ba điểm A, D, G thẳng hàng.
c) Tính DG biết AB = 13 cm, BC = 10 cm.
a, Xét tam giác ABH và tam giác ACH vuông tại H có: +, AB = AC ( vì tam giác ABC cân tại A)
+, AH chung
=> tam giác ABH = tam giác ACH (ch-cgv) => BH = CH = 6/2 = 3cm
b, Vì BH = CH => AH là đường trung tuyến của tam giác ABC => G nằm trên AH => A, G, H thẳng hàng
c, Vì tam giác ABH = tam giác ACH => góc BAH = góc CAH
Xét tam giác ABG và tam giác ACG có
AB = AC ( vì tam giác ABC cân tại A )
góc BAH = góc CAH ( chứng minh trên)
AG chung
=>tam giác ABG = tam giác ACG(c.g.c)
=> góc ABG = góc ACG
Cho tam giác ABC cân tại A đường cao CE.
a) tính AB biết BC=24 cm , BE=9 cm
b)gọi AD là đường cao và H là trục tâm của tam gics ABC . chứng minh CD2 = DH.DA
b: Ta có: ΔABC cân tại A
mà AD là đường cao
nên Dlà trung điểm của BC
Xét ΔCDH vuông tại D và ΔADB vuông tại D có
góc HCD=góc BAD
Do đó; ΔCDH đồng dạng với ΔADB
Suy ra: CD/AD=DH/DB
hay \(AD\cdot DH=CD^2\)
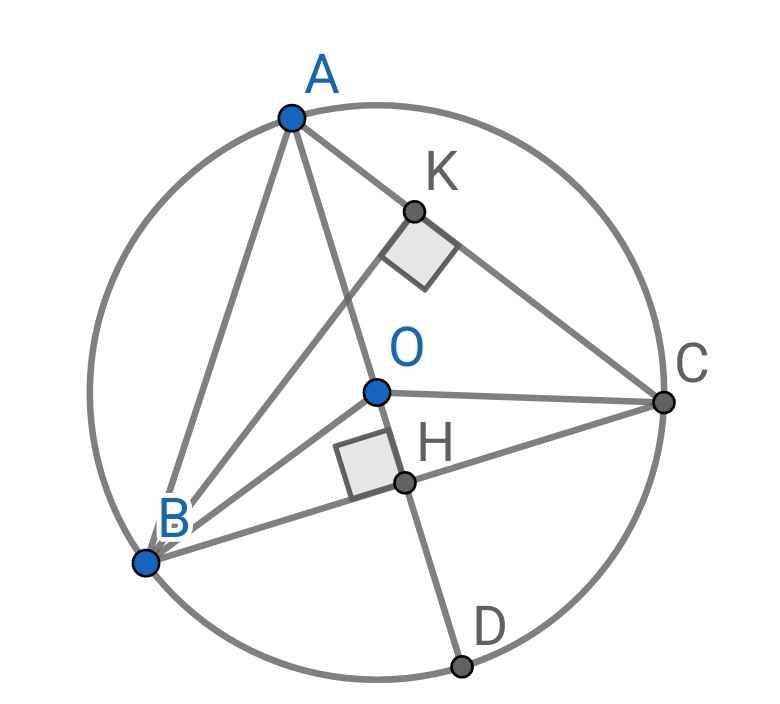
Cho tam giác ABC cân tại A nội tiếp đường tròn tâm O. Đường cao AH cắt đường tròn tại D
a) Vì sao AD lad đường kính của đường tròn tâm O
b) Cho biết AC = 10 cm, BC = 12 cm. Tính đường cao AH và BK của đường tròn tâm O
 a) Ta có:
a) Ta có:
OB = OC (bán kính)
⇒ O nằm trên đường trung trực của BC (1)
Do ∆ABC cân tại A (gt)
AH là đường cao (gt)
⇒ AH cũng là đường trung trực của ∆ABC
⇒ AH là đường trung trực của BC (2)
Từ (1) và (2) suy ra O ∈ AH
⇒ O ∈ AD
Vậy AD là đường kính của (O)
b) Sửa đề: Tính độ dài các đường cao AH, BK của ∆ABC
Do AH là đường trung trực của BC (cmt)
⇒ H là trung điểm của BC
⇒ CH = BC : 2
= 12 : 2
= 6 (cm)
∆AHC vuông tại H
⇒ AC² = AH² + CH² (Pytago)
⇒ AH² = AC² - CH²
= 10² - 6²
= 64
⇒ AH = 8 (cm)
⇒ sinACH = AH/AC
= 4/5
⇒ ACH ≈ 53⁰
⇒ BCK ≈ 53⁰
∆BCK vuông tại K
⇒ sinBCK = BK/BC
⇒ BK = BC.sinBCK
= 10.sin53⁰
≈ 8 (cm)
Cho tam giác ABC cân tại A biết ab bằng ac bằng 5 cm BC = 6 cm Hỏi đường cao AD và Be của tam giác ABC cắt nhau tại H D thuộc BC E thuộc AC
a Tính độ dài đoạn thẳng ad
B tính số đo góc C và góc ABC
C Gọi O là tâm đường tròn ngoại tiếp tam giác AC Chứng tỏ de là tiếp tuyến của đường tròn tâm O
Cho tam giác ABC cân tại A, đường cao AH và trung tuyến BK cắt nhau tại G. Tia CG cắt AB tại I
Cho tam giác ABC cân tại A; đường cao AH và trung tuyến BK cắt nhau tại G. Tia CG cắt AB tại I
a, Chứng minh tam giác AIG = tam giác AKG
b, Biết AH = 18 cm, BC = 16cm. Tính độ dài đoạn thẳng GI
c, Chứng minh IK // BC
Tham khảo
a) Ta có: AB = AC (gt); AI = IB = 1/2AB (Cmt); AK = KC = 1/2 AC (gt)
AB = AI + IB
AC = AK + KC
=> AI = AK
Ta lại có: t/giác ABC cân tại A; AH là đường cao
=> AH là đường p/giác (t/c của t/giác cân)
=> góc BAH = góc CAH
hay góc IAG = góc KAG
b) Xét t/giác IAG và t/giác KAG
có IA = AK (cmt)
góc IAG = góc KAG (cmt)
AG : chung
=> t/giác IAG = t/giác KAG (c.g.c)
c) Ta có: AI = AK (cm câu b)
=> t/giác AIK cân tại A
=> góc AIK = góc AKI = (180 độ - góc A)/2 (1)
Ta lại có: t/giác ABC cân tại A
=> góc B = góc C = (180 độ - góc A)/2 (2)
Từ (1) và (2) suy ra góc AIK = góc B
Mà góc AIK và góc B ở vị trí đồng vị
=> IK // BC
refer
a) Ta có: AB = AC (gt); AI = IB = 1/2AB (Cmt); AK = KC = 1/2 AC (gt)
AB = AI + IB
AC = AK + KC
=> AI = AK
Ta lại có: t/giác ABC cân tại A; AH là đường cao
=> AH là đường p/giác (t/c của t/giác cân)
=> góc BAH = góc CAH
hay góc IAG = góc KAG
b) Xét t/giác IAG và t/giác KAG
có IA = AK (cmt)
góc IAG = góc KAG (cmt)
AG : chung
=> t/giác IAG = t/giác KAG (c.g.c)
c) Ta có: AI = AK (cm câu b)
=> t/giác AIK cân tại A
=> góc AIK = góc AKI = (180 độ - góc A)/2 (1)
Ta lại có: t/giác ABC cân tại A
=> góc B = góc C = (180 độ - góc A)/2 (2)
Từ (1) và (2) suy ra góc AIK = góc B
Mà góc AIK và góc B ở vị trí đồng vị
=> IK // BC