Cho tam giác ABC vuông ở A, có AB = 6cm; AC = 8cm, phân giác BD. Kẻ DE vuông góc với BC (E thuộc BC). Gọi F là giao điểm của BA và ED
a) Tính độ dài cạnh BC?
b) Chứng minh DF = DC
c) Chứng minh D là trung trực của tam giác BFC
Cho tam giác ABC vuông ở A có và AB = 6cm. Tính các cạnh của tam giác.
vì trong tam giác vuông tại A nên =>AB=AC;B=C
vì AB=AC(cmt)=>AC=6cm
còn BC thì thì tui chịu
TK:
Định lí pi-ta-go
Ta giác ABC vuông tại A=> AB và AC là cạnh góc vuông còn BC là cạnh huyền
=>AB2+AC2=BC2
hay 62+82=BC2
=>100=BC2
=>BC2=102
=>BC=10cm
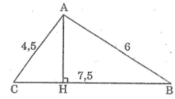
Cho tam giác ABC có AB = 6cm, AC = 4,5cm, BC = 7,5cm. Chứng minh tam giác ABC vuông ở A. Tính các góc B , C và đường cao AH của tam giác
Ta có:
A B 2 = 6 2 = 36 A C 2 = 4 , 52 = 20 , 25 B C 2 = 7 , 52 = 56 , 25
Vì A B 2 + A C 2 = 36 + 20,25 = 56,25 = B C 2 nên tam giác ABC vuông tại A (theo định lí đảo Pi-ta-go)
Kẻ AH ⊥ BC
Ta có: AH.BC = AB.AC
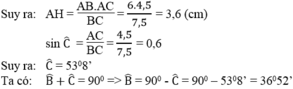
Cho tam giác ABC vuông tại A có AB=6cm,BC=10,phân giác BD.tính DA,DC
Cho tam giác ABC vuông tại A có AB=6cm,AC=10,phân giác AD.tính BC,DB,DC
Cho tam giác ABC vuông tại A có AB=6cm,BC=10,phân giác BD.tính DA,DC
Cho tam giác ABC vuông tại A có AB=6cm,AC=10,phân giác AD.tính BC,DB,DC
Cho tam giác ABC vuông ở A ,cạnh BC=7,5;AB=6cm . Gọi AH là đường cao của tam giác ABC. Tính CH
Xét tam giác ABC vuông tại A, đường cao AH
* Áp dụng hệ thức : \(AB^2=BH.BC=\left(BC-CH\right)BC\)
\(\Rightarrow36=\left(7,5-CH\right)7,5=56,25-7,5CH\)
\(\Leftrightarrow CH=\dfrac{27}{10}\)cm
cho hình tam giác abc vuông góc ở a, có cạnh ab =6cm,ac=8cm. Tính cạnh bc
yêu cầu các bạn ghi ra thứ tự lời giải rõ ràng.
Áp dụng đl Py-ta-go, ta có
BC^2=AB^2+AC^2
Mà AB^2=6^2=36,AC^2=8^2=64
=>BC^2=100=>BC=10
cho tam giác abc vuông ở a, có ab=6cm, ac=8cm, vẽ đường cao ah
a, tính bc
b, cm tam giác abc đồng dạng tam giác ahb
c, cm ab^2=bh.bc. tính bh, hc
d, vẽ phân giác ad của góc a( d thuộc bc). tính db
a) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=6^2+8^2=100\)
hay BC=10(cm)
Vậy: BC=10cm
b) Xét ΔABC vuông tại A và ΔHBA vuông tại H có
\(\widehat{HBA}\) chung
Do đó: ΔABC\(\sim\)ΔHBA(g-g)
c) Ta có: ΔABC\(\sim\)ΔHBA(cmt)
nên \(\dfrac{AB}{HB}=\dfrac{BC}{BA}\)(Các cặp cạnh tương ứng tỉ lệ)
hay \(AB^2=BH\cdot BC\)(đpcm)
Bài 2: Cho tam giác ABC vuông ở A, có AB = 6cm; AC = 8cm. Vẽ đường cao AH.
a) Tính BC.
b) Chứng minh AB2 = BH.BC
c) Tính BH; HC.
Bài 3: Cho hình chữ nhật ABCD có AB = 8cm, BC = 6cm. Vẽ đường cao AH của tam giác ADB, (H![]() BD)
BD)
a) Chứng minh DAHB ![]() DBCD.
DBCD.
b) Chứng minh AD2 = HD.DB.
c) Tính độ dài đoạn thẳng DH.
cíu oi, cíu đi gòi cho bắt zề nui, đi mà, cíuuuuuuuuuu ;-;
BẠN CÓ THỂ TRA THAY VÌ HỎI ĐC KO
thui hong cần nữa, hong cíu thì thui tui tự làm liu liu 
Cho tam giác ABC vuông góc A biết AB=6cm,BC=10cm, biết AB=6cm a)tính độ dài AC b) đường phân giác của góc ABC cắt cạnh AC ở E . Kẻ EH vuông góc BC (H thuộc BC). chứng minh rằng tam giác ABE= tam giác HBE c)gọi K là giao điểm của đường thẳng AB,HE. Chứng minh rằng tam giác EAC cân d) chứng minh đường thẳng BE là đường trung trực của AC
a) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow AC^2=BC^2-AB^2=10^2-6^2=64\)
hay AC=8(cm)
Vậy: AC=8cm
b) Xét ΔABE vuông tại A và ΔHBE vuông tại H có
BE chung
\(\widehat{ABE}=\widehat{HBE}\)(BE là tia phân giác của \(\widehat{ABH}\))
Do đó: ΔABE=ΔHBE(cạnh huyền-góc nhọn)
Cho tam giác ABC vuông ở A có AB=6CM;AC=8CM,kẻ đường cao AH
A) Tính độ dài BC
B) CM: Tam giác ABC đồng dạng với tam giác HBA
C) Tính độ dài các đoạn thẳng AH,BH,HC
a: BC=10cm
b: Xét ΔABC vuông tại A và ΔHBA vuông tại H có
\(\widehat{B}\) chung
Do đó: ΔABC∼ΔHBA
c: AH=4,8cm
BH=3,6cm
CH=6,4cm