Trong hệ trục tọa độ Oxy cho A(1;2) và M(m;\(m^2\)) Tìm m để 3 điểm phân biệt O A Mthẳng hàng
DH
Những câu hỏi liên quan
trong hệ trục tọa độ Oxy cho điểm A(2;3).Tọa độ của điểm B sao cho trục Ox là đường trung trực của đoạn thẳng AB
Trong không gian với hệ trục tọa độ Oxy, cho tam giác ABC biết
A
(
3
;
1
;
2
)
,
B
(
1
;
−
4
;
2
)
,
C
(
2
;
0
;
−
1
)
.
Tìm tọa độ tâm G của tam giác ABC A. G (2;-1;1). B. G (6;-3;3). C. G (2;1;1). D. G (2;-1;3).
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxy, cho tam giác ABC biết A ( 3 ; 1 ; 2 ) , B ( 1 ; − 4 ; 2 ) , C ( 2 ; 0 ; − 1 ) . Tìm tọa độ tâm G của tam giác ABC
A. G (2;-1;1).
B. G (6;-3;3).
C. G (2;1;1).
D. G (2;-1;3).
Trong không gian với hệ trục tọa độ Oxy, cho A(0;-1;1), B(-2;1;-1), C(-1;3;2). Biết rằng ABCD là hình bình hành, khi đó tọa độ điểm D là: A.
D
-
1
;
1
;
2
3
B.
D
1
;
3
;
4
C.
D...
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxy, cho A(0;-1;1), B(-2;1;-1), C(-1;3;2). Biết rằng ABCD là hình bình hành, khi đó tọa độ điểm D là:
A. D - 1 ; 1 ; 2 3
B. D 1 ; 3 ; 4
C. D 1 ; 4 ; 4
D. D - 1 ; - 3 ; - 2
Đáp án C
Ta có B A → = C D → ⇔ 2 ; - 2 ; 2 = x D + 1 ; y D - 3 ; z D - 2 ⇒ D 1 ; 1 ; 4 .
Đúng 0
Bình luận (0)
Trong mp với hệ tọa đô Oxy cho hai điểm A(1;-2), B(-4;5). Tìm tọa độ điểm M trên trục Oy sao cho 3 điểm M,A,B thẳng hàng
Gọi \(M\left(0;m\right)\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AM}=\left(-1;m+2\right)\\\overrightarrow{AB}=\left(-5;7\right)\end{matrix}\right.\)
3 điểm M;A;B thẳng hàng khi:
\(\dfrac{-1}{-5}=\dfrac{m+2}{7}\Rightarrow m=-\dfrac{3}{5}\)
\(\Rightarrow M\left(0;-\dfrac{3}{5}\right)\)
Đúng 2
Bình luận (0)
trong hệ tọa độ Oxy , cho 2 điểm A( 2;2 ) và B( 1;5 ) . tìm tọa độ điểm M trên trục tung sao cho độ dài MA + MB nhỏ nhất
Trong hệ tọa độ Oxy, cho hai điểm A(2; -3); B (3; 4) Tìm tọa độ điểm M thuộc trục hoành sao cho A, B, M thẳng hàng. A. M (1 ; 0) B. M(4; 0) C.
M
−
5
3
;
−
1
3
.
D.
M
17
7
;
0...
Đọc tiếp
Trong hệ tọa độ Oxy, cho hai điểm A(2; -3); B (3; 4) Tìm tọa độ điểm M thuộc trục hoành sao cho A, B, M thẳng hàng.
A. M (1 ; 0)
B. M(4; 0)
C. M − 5 3 ; − 1 3 .
D. M 17 7 ; 0 .
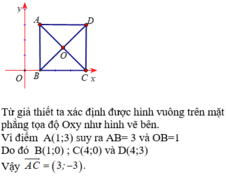
Trong hệ trục tọa độ Oxy, cho hình vuông ABCD tâm I và có A(1;3) . Biết điểm B thuộc trục Ox và
B
C
→
cùng hướng với
i
→
. Tìm tọa độ các vectơ
A
C
→
? A.(1;2) B.(3;4) C.(3;-3) D.(3;0)
Đọc tiếp
Trong hệ trục tọa độ Oxy, cho hình vuông ABCD tâm I và có A(1;3) . Biết điểm B thuộc trục Ox và B C → cùng hướng với i → . Tìm tọa độ các vectơ A C → ?
A.(1;2)
B.(3;4)
C.(3;-3)
D.(3;0)
trong hệ trục tọa độ Oxy cho 3 điểm A(-1;1) , B(1;3) , C(1;-1)
tìm tọa độ D sao cho A là trọng tâm tam giác BCD ??
gọi D(x;y)
A là trọng tâm của tam giác BCD ⇔\(\left\{{}\begin{matrix}-1=\dfrac{1+1+x}{3}\\1=\dfrac{3+\left(-1\right)+y}{3}\end{matrix}\right.\) ⇔\(\left\{{}\begin{matrix}x=-5\\y=1\end{matrix}\right.\) vậy D(-5;1)
Đúng 0
Bình luận (0)
Trong hệ trục tọa độ Oxy, cho tam giác ABC có A(2;–2), B(1;–1), C(5;2). Độ dài đường cao AH của tam giác ABC là
A. 3 5
B. 7 5
C. 9 5
D. 1 5
Chọn B.
*) AH là đường cao của tam giác ABC.
*) Lập phương trình cạnh BC
B(1;-1), C(5;2) 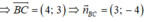
(BC): 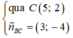
⇒ 3.(x - 5) - 4.(y - 2) = 0 ⇔ 3x - 15 - 4y + 8 = 0 ⇔ 3x - 4y - 7 = 0
Ta có:
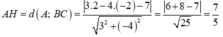
Đúng 0
Bình luận (0)
trong hệ trục tọa độ oxy cho A(1;2) B(-1;1) C(5;-1) tìm M sao cho |vectoMA + vectoMB + vectoMC | min