Giải phương trình
x^4 +2x^3 - 2x^2 + 2x -3 =0
Giải phương trình
a ) 2 x + 3 x - 4 = 2 x - 1 x + 2 - 27
b ) x 2 - 4 - x + 5 2 - x = 0
c ) x + 2 x - 2 - x - 2 x + 2 = 4 x 2 - 4
d ) x + 1 x - 1 - x + 2 x + 3 + 4 x 2 + 2 x - 3 = 0
a) 2(x + 3)(x – 4) = (2x – 1)(x + 2) – 27
⇔ 2(x2 – 4x + 3x – 12) = 2x2 + 4x – x – 2 – 27
⇔ 2x2 – 2x – 24 = 2x2 + 3x – 29
⇔ -2x – 3x = 24 – 29
⇔ - 5x = - 5 ⇔ x = -5/-5 ⇔ x = 1
Tập nghiệm của phương trình : S = {1}
b) x2 – 4 – (x + 5)(2 – x) = 0
⇔ x2 – 4 + (x + 5)(x – 2) = 0 ⇔ (x – 2)(x + 2 + x + 5) = 0
⇔ (x – 2)(2x + 7) = 0 ⇔ x – 2 = 0 hoặc 2x + 7 = 0
⇔ x = 2 hoặc x = -7/2
Tập nghiệm của phương trình: S = {2; -7/2 }
c) ĐKXĐ : x – 2 ≠ 0 và x + 2 ≠ 0 (khi đó : x2 – 4 = (x – 2)(x + 2) ≠ 0)
⇔ x ≠ 2 và x ≠ -2
Quy đồng mẫu thức hai vế :
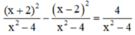
Khử mẫu, ta được : x2 + 4x + 4 – x2 + 4x – 4 = 4
⇔ 8x = 4 ⇔ x = 1/2( thỏa mãn ĐKXĐ)
Tập nghiệm của phương trình : S = {1/2}
d) ĐKXĐ : x – 1 ≠ 0 và x + 3 ≠ 0 (khi đó : x2 + 2x – 3 = (x – 1)(x + 3) ≠ 0)
⇔ x ≠ 1 và x ≠ -3
Quy đồng mẫu thức hai vế :
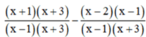
![]()
Khử mẫu, ta được : x2 + 3x + x + 3 – x2 + x – 2x + 2 + 4 = 0
⇔ 3x = -9 ⇔ x = -3 (không thỏa mãn ĐKXĐ)
Tập nghiệm của phương trình : S = ∅
\(2\left(x+3\right)\left(x-4\right)=\left(2x-1\right)\left(x+2\right)-27\)
\(< =>2\left(x^2-x-12\right)=2x^2+3x-2-27\)
\(< =>2x^2-2x-24=2x^2+3x-2-27\)
\(< =>5x=-24+29=5\)
\(< =>x=\frac{5}{5}=1\)
\(x^2-4-\left(x+5\right)\left(2-x\right)=0\)
\(< =>\left(x-2\right)\left(x+2\right)+\left(x+5\right)\left(x-2\right)=0\)
\(< =>\left(x-2\right)\left(x+2+x+5\right)=0\)
\(< =>\left(x-2\right)\left(2x+7\right)=0\)
\(< =>\orbr{\begin{cases}x-2=0\\2x+7=0\end{cases}}< =>\orbr{\begin{cases}x=2\\x=-\frac{7}{2}\end{cases}}\)
giải phương trình sau: x^4-2x^3+x-căn (2x^2-2x)=0
Đầu tiên ta đặt dk 2x^2 - 2x >=0 <=> x<=0 và x>=1
x^4 -2x^3+x - căn(2x^2-2x)=0
<=> x(x^3-2x^2+1) - căn[2x(x-1)]=0
<=>x[(x^3-x^2)-(x^2-1)] - căn[2x(x-1)]=0
<=>x[x^2(x-1)-(x-1)(x+1)] - căn[2x(x-1)]=0
<=>x(x-1)(x^2-x-1) - căn[2x(x-1)]=0
<=>x(x-1)[x(x-1)-1] - căn[2x(x-1)]=0
<=>[x(x-1)]^2 -x(x-1) - căn[2x(x-1)]=0(*)
Nhân cả hai vế của pt(*) cho 4 ta được:
4[x(x-1)]^2 -4x(x-1) - 4căn[2x(x-1)]=0(**)
Đến đây ta đặt t=căn[2x(x-1)] điều kiện t>=0 ta được pt sau
t^4 -2t^2 -4t =0
<=> t(t^3 - 2t -4)=0
<=> t=0 hoặc t^3-2t -4=0
với t=0 thế vào t= căn[2x(x-1)]=0 => x=0 hoặc x=1
với t^3-2t-4=0 ta thấy pt này có một nghiệm t=2
<=> (t-2)(t^2+2t+2)=0(ở đây ta thực hiện chia t^3-2t-4 cho t-2)
<=>t=2
thế t=2 vào t=căn[2x(x-1)]=2 ta tìm được x=-1 hoặc x=2
thỏa mãn dk x<=0 và x>=1
Vậy pt đã cho có các nghiệm sau x=0; x=1; x=-1; x=2
Kết luận: x=0; x=1; x=-1; x=2
Giải phương trình : \(x^4+2x^3-2x^2+2x-3=0\)
\(x^4+2x^3-2x^2+2x-3=0\Leftrightarrow\left(x-1\right)\left(x+3\right)\left(x^2+1\right)=0\Leftrightarrow\orbr{\begin{cases}x=1\\x=3\end{cases}}\)
x^4-x^3+3x^3-3x^2+x^2-x+3x-3=0
(x^3+3x^2+x+1)(x-1)=0
.......
x4 + 2x3 - 2x2 - 3 =0
(=) x4 + 3x3 - x3 - 3x2 + x2 + 3x -x - 3 =0
(=) x3(x+3) - x2(x+3) + x(x+3) - (x+3) = 0
(=) (x+3) . (x3 - x2 + x -1 ) =0
(=) (x+3) . [x2(x-1) + (x-1)] = 0
(=) (x+3).(x-1).(x2 + 1) = 0
TH1 : x2 + 1 = 0 TH2: \(\orbr{\begin{cases}x+3=0\\x-1=0\end{cases}}\)(=) \(\orbr{\begin{cases}x=-3\\x=1\end{cases}}\)
(=) x2 = -1 (loại )
Vậy phương trình có nghiệm là : x = -3 , x = 1
Bài 1
:Cho h
ệ
phương trình
x (a 3)y 0
(a 2)x 4y a 1
(a là tham s
ố
).
1, Gi
ả
i h
ệ
phương trình v
ớ
i a = 2; a =
-
1.
2, Tìm a đ
ể
h
ệ
có nghi
ệ
m duy nh
ấ
t (x ; y) th
ỏ
a mãn: 2x + 3y > 5.
Giải các phương trình sau a.(2x-5)(12+5x)=0 b(x-3)(x-4)-2(x-3=0 c.x(x-1)(x+1)=0 dù.2x/3+2x-1/6=0
`a,(2x-5)(12+5x)=0`
\(\Leftrightarrow\left[{}\begin{matrix}2x-5=0\\12+5x=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}2x=5\\5x=-12\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{5}{2}\\x=-\dfrac{12}{5}\end{matrix}\right.\)
`b, (x-3)(x-4)-2(x-3)=0`
`<=>(x-3)(x-4-2)=0`
`<=>(x-3)(x-6)=0`
\(\Leftrightarrow\left[{}\begin{matrix}x-3=0\\x-6=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=3\\x=6\end{matrix}\right.\)
`c, x(x-1)(x+1)=0`
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x-1=0\\x+1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=1\\x=-1\end{matrix}\right.\)
`d, (2x)/3 +(2x-1)/6=0`
`<=> (4x)/6 +(2x-1)/6=0`
`<=> (4x+2x-1)/6=0`
`<=> (6x-1)/6=0`
`<=> 6x-1=0`
`<=> 6x=1`
`<=>x=1/6` ( đề là vậy à bạn )
a) \(\left(2x-5\right)\left(12+5x\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-5=0\\12+5x=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}2x=5\\5x=-12\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=2,5\\x=-2,4\end{matrix}\right.\)
b) \(\left(x-3\right)\left(x-4\right)-2\left(x-3\right)=0\)
\(\Leftrightarrow\left(x-3\right)\left[\left(x-4\right)-2\right]=0\)
\(\Leftrightarrow\left(x-3\right)\left(x-6\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}x-3=0\\x-6=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=3\\x=6\end{matrix}\right.\)
c) \(x\left(x-1\right)\left(x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x+1=0\\x-1=0\\x=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-1\\x=1\\x=0\end{matrix}\right.\)
d) \(\dfrac{2x}{3}+\dfrac{2x-1}{6}=0\)
\(\Leftrightarrow\dfrac{4x+2x-1}{6}=0\)
\(\Leftrightarrow6x-1=0\)
\(\Leftrightarrow6x=1\Leftrightarrow x=\dfrac{1}{6}\)
giải phương trình sau
1/ 2x( x+3) - 6 (x-3) =0
2/ 2x^2( 2x+3) +(2x+3) =0
3/ (x-2) (x+1) -(x-2) 4x =0
4/ 2x ( x-5) -3x +15=0
5/ 3x(x+4) -2x-8 =0
6/ x^2 (2x-6) + 2x -6 =0
1: Ta có: \(2x\left(x+3\right)-6\left(x-3\right)=0\)
\(\Leftrightarrow2x^2+6x-6x+18=0\)
\(\Leftrightarrow2x^2+18=0\left(loại\right)\)
2: Ta có: \(2x^2\left(2x+3\right)+\left(2x+3\right)=0\)
\(\Leftrightarrow2x+3=0\)
hay \(x=-\dfrac{3}{2}\)
3: Ta có: \(\left(x-2\right)\left(x+1\right)-4x\left(x-2\right)=0\)
\(\Leftrightarrow\left(x-2\right)\left(1-3x\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2\\x=\dfrac{1}{3}\end{matrix}\right.\)
4: Ta có: \(2x\left(x-5\right)-3x+15=0\)
\(\Leftrightarrow\left(x-5\right)\left(2x-3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=5\\x=\dfrac{3}{2}\end{matrix}\right.\)
5: Ta có: \(3x\left(x+4\right)-2x-8=0\)
\(\Leftrightarrow\left(x+4\right)\left(3x-2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-4\\x=\dfrac{2}{3}\end{matrix}\right.\)
6: Ta có: \(x^2\left(2x-6\right)+2x-6=0\)
\(\Leftrightarrow2x-6=0\)
hay x=3
Giải bất phương trình sau : a/ 2x ^ 2 + 6x - 8 < 0 x ^ 2 + 5x + 4 >=\ 2) Giải phương trình sau : a/ sqrt(2x ^ 2 - 4x - 2) = sqrt(x ^ 2 - x - 2) c/ sqrt(2x ^ 2 - 4x + 2) = sqrt(x ^ 2 - x - 3) b/ x ^ 2 + 5x + 4 < 0 d/ 2x ^ 2 + 6x - 8 > 0 b/ sqrt(- x ^ 2 - 5x + 2) = sqrt(x ^ 2 - 2x - 3) d/ sqrt(- x ^ 2 + 6x - 4) = sqrt(x ^ 2 - 2x - 7)
2:
a: =>2x^2-4x-2=x^2-x-2
=>x^2-3x=0
=>x=0(loại) hoặc x=3
b: =>(x+1)(x+4)<0
=>-4<x<-1
d: =>x^2-2x-7=-x^2+6x-4
=>2x^2-8x-3=0
=>\(x=\dfrac{4\pm\sqrt{22}}{2}\)
Giải phương trình:
\(\sqrt{2x-2\sqrt{2x-1}}-2\sqrt{2x+3-4\sqrt{2x-1}}+3\sqrt{2x+8-6\sqrt{2x-1}}=0\)
Điều kiện: \(x\ge\dfrac{1}{2}\)
\(\sqrt{2x-2\sqrt{2x-1}}-2\sqrt{2x+3-4\sqrt{2x-1}}+3\sqrt{2x+8-6\sqrt{2x-1}=0}\)
\(\Leftrightarrow\sqrt{\left(\sqrt{2x-1}-1\right)^2}-2\sqrt{\left(\sqrt{2x-1}-2\right)^2}+3\sqrt{\left(\sqrt{2x-1}-3\right)^2}=0\)
\(\Leftrightarrow\left|\sqrt{2x-1}-1\right|-2\left|\sqrt{2x-1}-2\right|+3\left|\sqrt{2x-1}-3\right|=0\)
Với \(\dfrac{1}{2}\le x< 1\)
\(\Leftrightarrow1-\sqrt{2x-1}-2\left(2-\sqrt{2x-1}\right)+3\left(3-\sqrt{2x-1}\right)=0\)
\(\Leftrightarrow-2\sqrt{2x-1}+6=0\)
\(\Leftrightarrow x=5\left(l\right)\)
Tương tự cho các trường hợp: \(1\le x< \dfrac{5}{2};\dfrac{5}{2}\le x< 5;x\ge5\)
Tới đây thì kết luận thôi.
\(\sqrt{2x-2\sqrt{2x-1}}-2\sqrt{2x+3-4\sqrt{2x-1}}+3\sqrt{2x+8-6\sqrt{2x-1}}=0\)
ĐK:\(x\ge\dfrac{1}{2}\)
\(\Leftrightarrow\sqrt{2x-1-2\sqrt{2x-1}+1}-2\sqrt{2x-1-4\sqrt{2x-1}+4}+3\sqrt{2x-1-6\sqrt{2x-1}+9}=0\)
\(\Leftrightarrow\sqrt{\left(\sqrt{2x-1}-1\right)^2}-2\sqrt{\left(\sqrt{2x-1}-2\right)^2}+3\sqrt{\left(\sqrt{2x-1}-3\right)^2}=0\)
\(\Leftrightarrow\sqrt{2x-1}-1-2\left(\sqrt{2x-1}-2\right)+3\left(\sqrt{2x-1}-3\right)=0\)
\(\Leftrightarrow\sqrt{2x-1}-1-2\sqrt{2x-1}+4+3\sqrt{2x-1}-9=0\)
\(\Leftrightarrow2\sqrt{2x-1}-6=0\)\(\Leftrightarrow\sqrt{2x-1}=3\)
\(\Leftrightarrow2x-1=9\Leftrightarrow2x=10\Rightarrow x=5\) *Thỏa*