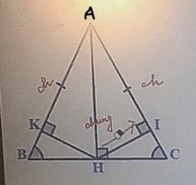
a)chứng minh: BH=HC;
góc BAH=góc CAH
b)tam giác HKB=tam giác HIC
H24
Những câu hỏi liên quan
Cho tam giác ABC vuông tại A kẽ đường cao AH a) Chứng minh ∆ABC~∆HAC b) Chứng minh AC bình phương = BC•HC c) Biết BH= 9cm HC= 16cm , tính độ dài các cạnh AB , AC
Do là mình chưa đọc kĩ đề nên là vẽ cạnh BH và CH nó bị sai tỉ lệ, bạn nên vẽ cạnh AC dài ra để hai cạnh đó đúng tỉ lệ nha.
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A; đường cao AH ( H thuộc BC ) và phân giác CM ( M thuộc AB ). N là giao điểm AH và CM. Biết BH = 3cm; HC = 27cm. Chứng minh AH2 = BH x HC
cho ΔABC cân tại A , vẽ AH ⊥ BC tại H . Biết AB = 5 cm , BC = 6 cm .
a, Chứng minh BH = HC
b, Tính đọ dài BH , AH
c, Gọi G là trọng tâm của △ABC . Chứng minh rằng A,G,H thẳng hàng
a: ΔABC cân tại A có AH là đường cao
nên H là trung điểm của BC
=>HB=HC
b: HB=HC=6/2=3cm
=>AH=căn 5^2-3^2=4cm
c: G là trọng tâm của ΔABC
=>AG là trung tuyến ứng với cạnh BC trongΔABC
=>A,G,H thẳng hàng
Đúng 0
Bình luận (0)
Cho tam giác vuông tại A có AC>AB , vẽ AH vuông góc BC tại H . Chứng minh a ) Góc B > C b) HC>HB( chứng minh bằng 2 cách ) c) Góc B = góc HAC và góc C=HAB d) HC>AH và AH>BH
a: Xét ΔABC có AC>AB
nên góc B>góc C
b: Xét ΔABC có AB<AC
mà HB,HC lần lượt là hình chiếu của AB,AC trên BC
nên HB<HC
c: góc B+góc C=90 độ
góc HAC+góc C=90 độ
=>góc B=góc HAC
góc C+góc B=90 độ
góc HAB+góc B=90 độ
=>góc C=góc HAB
Đúng 0
Bình luận (0)
Bài 3 Cho ΔABC cân tại A. Kẻ BH vuông góc với AC, CK vuông góc với AB. Gọi M là giao điểm của của BH và CK. a) Chứng minh AH = AK. b) Chứng minh AM là tia phân giác của góc A. c) Chứng minh KH // BC.
mình mới hc tới bài pitago '
a: Xét ΔABH vuông tại H và ΔACK vuông tại K có
AB=AC
\(\widehat{BAH}\) chung
Do đó:ΔABH=ΔACK
Suy ra: AH=AK
b: Xét ΔKBC vuông tại K và ΔHCB vuông tại H có
BC chung
KC=HB
Do đó:ΔKBC=ΔHCB
Suy ra: \(\widehat{MBC}=\widehat{MCB}\)
hayΔMBC cân tại M
Xét ΔABM và ΔACM có
AB=AC
AM chung
BM=CM
Do đó:ΔABM=ΔACM
Suy ra: \(\widehat{BAM}=\widehat{CAM}\)
hay AM là tia phân giác của góc A
c: Xét ΔABC có AK/AB=AH/AC
nên KH//BC
Đúng 0
Bình luận (0)
Cho ∆ABC vuông ở A, có AB=5cm, AC=4cm. Vẽ đường cao AH: a, Chứng minh ∆HBA~∆ABC b, Chứng minh AB2 = BH×BC. Tính BH×HC c, Trên AH lấy điểm K sao cho AK=1,2cm. Từ K vẽ đường thẳng song song BC cắt AB và AC lần lượt tại M và N. Tính diện tích tứ giác BMNC
a: Xet ΔHBA vuông tại H và ΔABC vuông tại A có
góc B chung
=>ΔHBA đồng dạng với ΔABC
b: ΔHBA đồng dạng với ΔABC
=>BH/BA=BA/BC
=>BA^2=BH*BC
Đúng 1
Bình luận (0)
Cho tam giác ABC vuông tại A; đường cao AH ( H thuộc BC ) và phân giác CM ( M thuộc AB ). N là giao điểm AH và CM. Biết BH = 3cm; HC = 27cm. Chứng minh AH2 = BH x HC.
Gọi AM trung tuyến tam giác ABC. BH và CK là 2 đường cao của tam giác ABM và tam giác ACM
a) Chứng minh BH // CK
b) Chứng minh trung điểm HK
c) Chứng minh HC // BK
TN
6 tháng 11 2021 lúc 16:23
Cho ΔABC vuông tại B, vẽ đường cao BH sao cho AH = 4cm, HC = 2cm.
a) tính BH
b) tính số đo góc A
c) chứng minh rằng \(S_{ABC}=\dfrac{BH^2}{2sinA.sinC}\)
a, Áp dụng HTL: \(BH=\sqrt{AH\cdot HC}=2\sqrt{2}\left(cm\right)\)
b, \(\tan A=\dfrac{BH}{AH}=\dfrac{\sqrt{2}}{2}\approx35^0\Leftrightarrow\widehat{A}\approx35^0\)
c, Áp dụng HTL: \(BH\cdot AC=AB\cdot BC\Leftrightarrow BH^2\cdot AC^2=AB^2\cdot BC^2\)
\(\dfrac{BH^2}{2\sin A\cdot\sin C}=BH^2\cdot\dfrac{1}{\dfrac{2BC\cdot AB}{AC^2}}=\dfrac{1}{2}\cdot\dfrac{BH^2\cdot AC^2}{BC\cdot AB}=\dfrac{1}{2}\cdot\dfrac{AB^2\cdot BC^2}{AB\cdot BC}=\dfrac{1}{2}AB\cdot BC=S_{ABC}\)
Đúng 1
Bình luận (0)