a ,   Δ A B C ,   A ⏜ = 90 0 , A H ⊥ B C g t ⇒ A H = B H . C H = 4.9 = 6 c m Δ A B H ,   H ⏜ = 90 0   g t ⇒ tan B = A H B H = 6 4 ⇒ B ⏜ ≈ 56 , 3 0 b ,   Δ A B C ,   A ⏜ = 90 0 , M B = M C g t ⇒ A M = 1 2 B C = 1 2 .13 = 6 , 5 c m S Δ A H M = 1 2 M H . A H = 1 2 .2 , 5.6 = 7 , 5 c m 2

a, Xét Δ ABC và Δ CBH

Ta có : \(\widehat{ACB}=\widehat{CHB}=90^o\)

            \(\widehat{ABC}=\widehat{CBH}\) (góc chung)

=> Δ ABC ∾ Δ CBH (g.g)

b, Ta có : Δ ABC ∾ Δ CBH (cmt)

=> \(\dfrac{AB}{CB}=\dfrac{BC}{BH}\)

=> \(BC^2=AB.BH\)

c,

Ta có : AB = AH + HB

=> AB = 4 + 9

=> AB = 13 (cm)

Ta có : \(BC^2=AB.BH\left(cmt\right)\)

=> \(BC^2=13.9\)

=> \(BC^2=117\)

=> BC = 10,8 (cm)

Xét Δ ABC

Ta có : \(AB^2=AC^2+BC^2\)

=> \(13^2=AC^2+10,8^2\)

=> \(169=AC^2+116,64\)

=> \(169-116,64=AC^2\)

=> \(52,36=AC^2\)

=> AC = 7,2 (cm)

Xét Δ ABC vuông tại C

=> \(S_{\Delta ABC}=\dfrac{AC.BC}{2}\)

=> \(S_{\Delta ABC}=\dfrac{7,2.10,8}{2}\)

=> \(S_{\Delta ABC}=38,88\left(cm^2\right)\)

a, Xét Δ ABC và Δ CBH

Ta có : 

             (góc chung)

=> Δ ABC ∾ Δ CBH (g.g)

b, Ta có : Δ ABC ∾ Δ CBH (cmt)

=> ABCB=BCBHABCB=BCBH

=> BC2=AB.BH

c,

Ta có : AB = AH + HB

=> AB = 4 + 9

=> AB = 13 (cm)

Ta có : BC2=AB.BH(cmt)BC2=AB.BH(cmt)

=> BC2=13.9BC2=13.9

=> BC2=117BC2=117

=> BC = 10,8 (cm)

Xét Δ ABC

Ta có : AB2=AC2+BC2AB2=AC2+BC2

=> 132=AC2+10,82132=AC2+10,82

=> 169=AC2+116,64169=AC2+116,64

=> 169−116,64=SΔABC=7,2.10,82SΔABC=7,2.10,82

=> SΔABC=38,88(cm2)

Bạn chỉ cần áp dụng hệ thức lượng là đc rồi o0o

Cho tam giác ABC vuông tại A , đường cao AH . Chứng minh rằng 1/AH^2=1/AB^2+1/ac^2

a: \(AH=4\sqrt{3}\left(cm\right)\)

HC=12cm

BC=16cm

Áp dụng hệ thức lượng trong tam giác ABC vuông tại A

Ta có: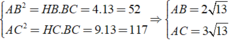

Vậy S A B C   =   1 2 A B . A C   =   1 2 . 2 13   . 3 13 =   39 c m 2

Chọn đáp án A.

Áp dụng định lý Pitago:

\(AB=\sqrt{AH^2+BH^2}=\sqrt{41}\)

Áp dụng hệ thức lượng:

\(AB^2=BH.BC\Rightarrow BC=\dfrac{AB^2}{BH}=\dfrac{41}{4}\)

Áp dụng Pitago:

\(AC=\sqrt{BC^2-AB^2}=\dfrac{5\sqrt{41}}{4}\)

Chu vi: \(AB+AC+BC=\dfrac{41+9\sqrt{41}}{4}\left(cm\right)\)

a,

Xét Δ AHB và Δ CAB, có :

\(\widehat{AHB}=\widehat{CAB}=90^o\)

\(\widehat{ABH}=\widehat{CBA}\) (góc chung)

=> Δ AHB ∾ Δ CAB (g.g)

=> \(\dfrac{AH}{CA}=\dfrac{HB}{AB}\)

=> \(\dfrac{AB}{CA}=\dfrac{HB}{AH}\)

Xét Δ AHB và Δ CHA, có :

\(\widehat{AHB}=\widehat{CHA}=90^o\)

\(\dfrac{AB}{CA}=\dfrac{HB}{AH}\) (cmt)

=> Δ AHB ∾ Δ CHA (g.g)

=> \(\dfrac{AH}{CH}=\dfrac{HB}{HA}\)

=> \(AH^2=HB.CH\)

b, Ta có : \(AH^2=BH.CH\) (cmt)

=> \(AH^2=4.9\)

=> \(AH^2=36\)

=> AH = 6

Xét Δ AHB, có :

\(AB^2=AH^2+BH^2\)

=> \(AB^2=6^2+4^2\)

=> \(AB^2=52\)

=> AB = 7,2 (cm)

Xét Δ AHC, có :

\(AC^2=AH^2+CH^2\)

=> \(AC^2=6^2+9^2\)

=> \(AC^2=117\)

=> AC = 10,8 (cm)

Xét Δ ABC, có :

\(BC^2=AB^2+AC^2\)

=> \(BC^2=7,2^2+10,8^2\)

=> \(BC^2=168,48\)

=> BC = 12,9 (cm)

Ta có : MC = \(\dfrac{1}{2}BC\) (M là trung điểm BC do có đường trung tuyến AM)

=> MC = 6,45 (cm)

Ta có : BC = BH + HM + MC

=> 12,9 = 4 + HM + 6,45

=> HM = 12,9 - 4 - 6,45

=> HM = 2,45 (cm)

Xét Δ AMH vuông tại H, có :

\(S_{\Delta AMH}=\dfrac{1}{2}AH.HM\)

=> \(S_{\Delta AMH}=\dfrac{1}{2}.6.2,45\)

=> \(S_{\Delta AMH}=7,35\left(cm\right)\)

BÀI 2 : áp dụng hệ thức lượng trong tam giác, ta có: AH^2=BH*CH=>AH^2= 4*9=36=>AH=căn bậc hai của 36=6

\(AB^2=BH\cdot BC=4\cdot\left(4+9\right)=52=>AB=\sqrt{52}=2\sqrt{13}\)

\(AC^2=CH\cdot BC=9\cdot13=117=>AC=\sqrt{117}=3\sqrt{13}\)

Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:

\(AH^2=BH\cdot CH\)

\(\Leftrightarrow AH^2=4\cdot9=36\)

hay AH=6(cm)

Ta có: BH+CH=BC(H nằm giữa B và C)

nên BC=4+9=13(cm)

Ta có: ΔABC vuông tại A(gt)

mà AM là đường trung tuyến ứng với cạnh huyền BC(M là trung điểm của BC)

nên \(AM=\dfrac{1}{2}BC\)(Định lí 1 về áp dụng hình chữ nhật vào tam giác vuông)

hay \(AM=\dfrac{1}{2}\cdot13=6.5\left(cm\right)\)

Áp dụng định lí Pytago vào ΔAMH vuông tại H, ta được:

\(AM^2=AH^2+MH^2\)

\(\Leftrightarrow MH^2=AM^2-AH^2=6.5^2-6^2=6.25\)

hay MH=2,5(cm)

Diện tích tam giác AMH là:

\(S_{AMH}=\dfrac{AH\cdot HM}{2}=\dfrac{6\cdot2.5}{2}=\dfrac{15}{2}=7.5\left(cm^2\right)\)