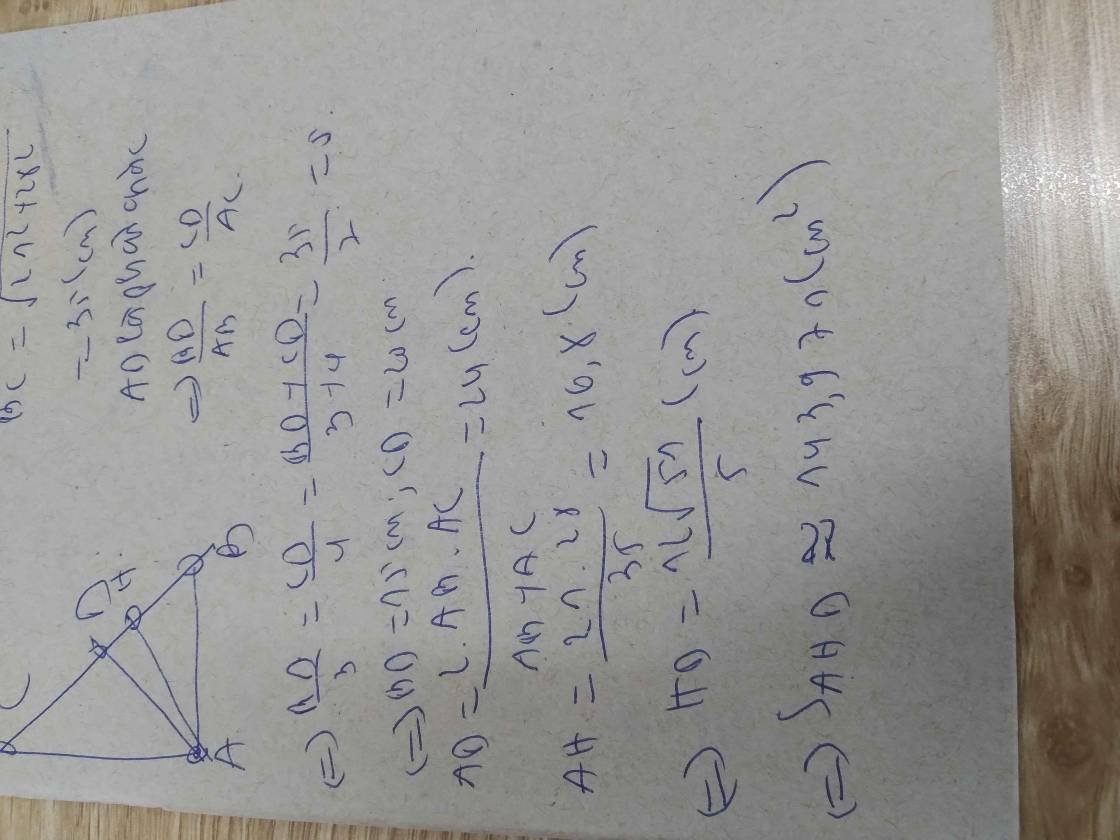Cho tam giác ABC vuông tại A có đường cao AH (H thuộc BC) Vẽ (A;AH) vẽ đường kính HD.Qua D vẽ tiếp tuyến với đường tròn,tiếp tuyến này cắt BA kéo dài tại điểm E
a)CMR: tam giác ADE=tam giác AHB
b)tam giác CBE cân
c) Gọi I là hình chiếu của A trên CE.CMR:CE là tiếp tuyến của đường tròn (A;AH)