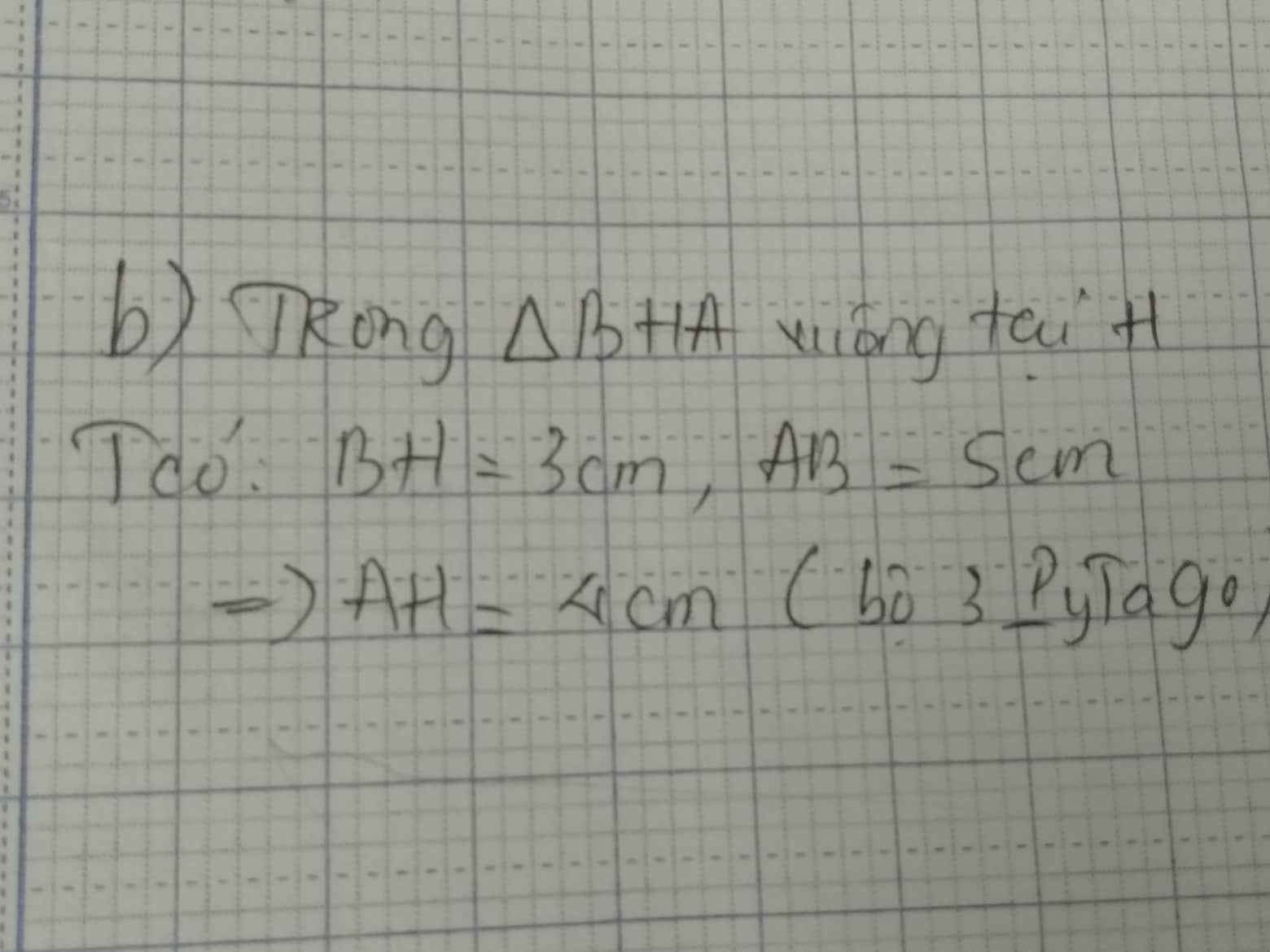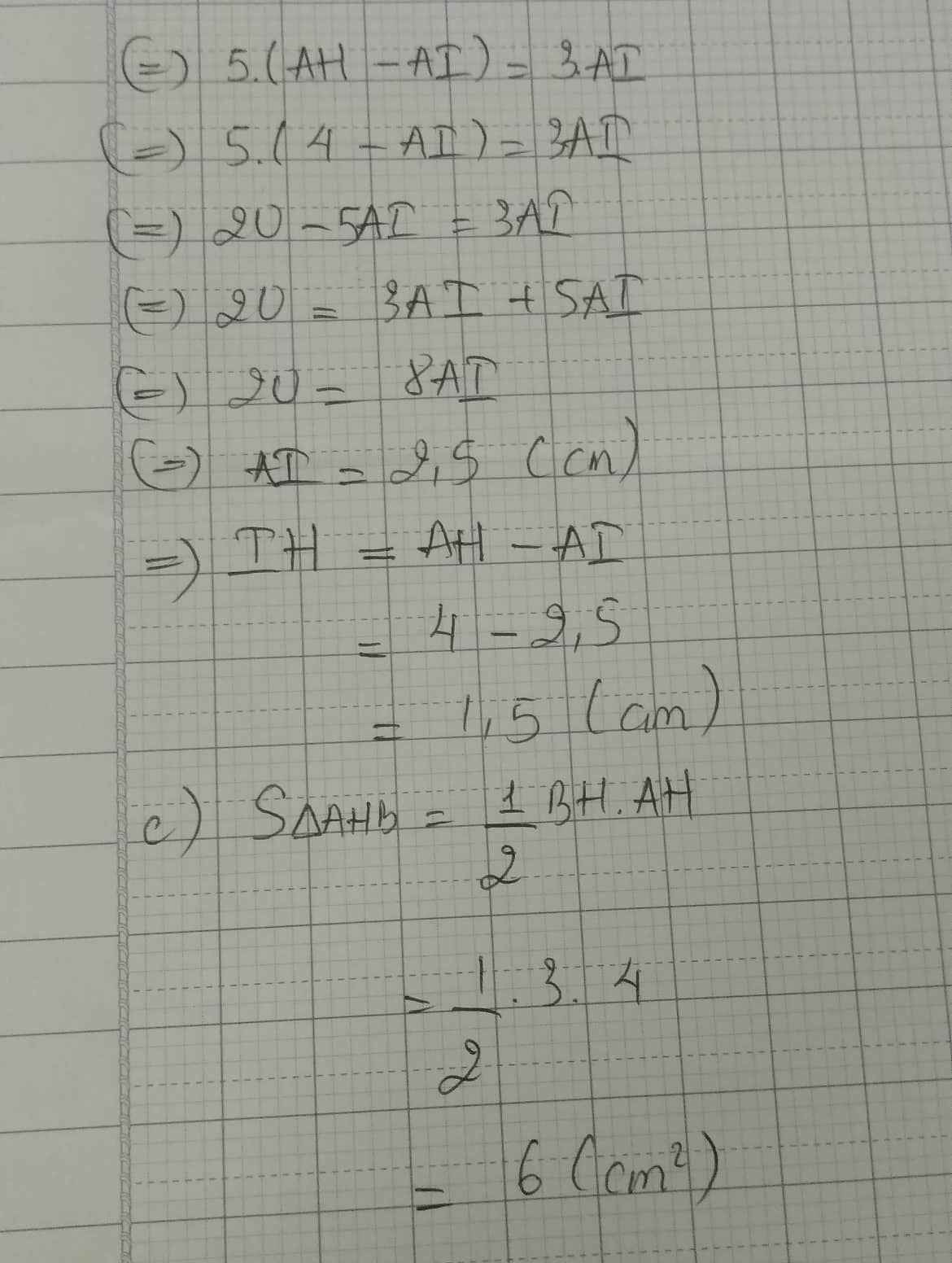Cho tam giác ABC VUÔNG TẠI a, đường cao AH
a) Biết AB;AC=3:4 và BC=125. Tính BH,CH
b)Biết AB:AC=5:6 và AH=30. Tính BH,CH
HB
Những câu hỏi liên quan
1, Cho tam giác ABC vuông tại A,đường cao AH
a, Cho biêt AB=3cm,BC=5cm.Tính độ dài đoạn thẳng BH,CH,AH và AC
b,Cho biết AH=60cm,CH=144cm.Tính độ dài đoạn thẳng AB,AC,BC và BH
2, Cho tam giác ABC vuông tại A, đường cao AH
Cho biết \(\dfrac{AB}{AC}\)=\(\dfrac{5}{6}\) và BC=122cm.Tính độ dài các đoạn thẳng BH,CH
Bài 2:
Ta có: \(\dfrac{AB}{AC}=\dfrac{5}{6}\)
\(\Leftrightarrow\dfrac{HB}{HC}=\dfrac{25}{36}\)
\(\Leftrightarrow HB=\dfrac{25}{36}HC\)
Ta có: HB+HC=BC
\(\Leftrightarrow HC\cdot\dfrac{61}{36}=122\)
\(\Leftrightarrow HC=72\left(cm\right)\)
hay HB=50(cm)
Đúng 1
Bình luận (0)
cho tam giác ABC vuông tại A, đường cao AH
a, biết AH = 6cm, BH = 4,5cm. Tính AB, AC, BC, HC
b, biết AB = 6cm, BH = 3cm. Tính AH, AC, CH
\(a,\) Áp dụng HTL tam giác
\(\left\{{}\begin{matrix}AH^2=BH\cdot HC\\AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}CH=\dfrac{AH^2}{BH}=\dfrac{36}{4,5}=8\left(cm\right)\\AB=\sqrt{4,5\left(4,5+8\right)}=\sqrt{4,5\cdot12,5}=7,5\left(cm\right)\\AC=\sqrt{8\cdot12,5}=10\left(cm\right)\end{matrix}\right.\)
và \(BC=12,5\left(cm\right)\)
\(b,\) Áp dụng HTL tam giác
\(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\\AH^2=CH\cdot BH\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}BC=\dfrac{AB^2}{BH}=\dfrac{36}{3}=12\left(cm\right)\\CH=\dfrac{AC^2}{BC}=\dfrac{BC^2-AB^2}{12}=\dfrac{6\sqrt{3}}{12}=\dfrac{\sqrt{3}}{2}\left(cm\right)\\AH=3\cdot\dfrac{\sqrt{3}}{2}=\dfrac{3\sqrt{3}}{2}\left(cm\right)\end{matrix}\right.\)
Đúng 2
Bình luận (0)
Cho tam giác ABC vuông tại A (AB > AC), đường cao AH
a) Chứng minh: \(\dfrac{AB^2}{BH}=\dfrac{AC^2}{CH}\)
b) Biết \(\widehat{C}\) \(=60^0\), AC = 8, AB = 12. Giải tam giác HAB
a: ΔABC vuông tại A có AH là đường cao
nên AB^2=BH*BC; AC^2=CH*CB
=>AB^2/AC^2=BH/CH
b:
góc B=90-60=30 độ
góc HAB=90-30=60 độ
BC=căn 8^2+12^2=4*căn 13(cm)
HB=AB^2/BC=36/căn 13(cm)
AH=8*12/4*căn 13=24/căn 13(cm)
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A(AB<AC). Kẻ đường cao AH
a. Chứng minh:AB2/AC2 =BH/CH
Áp dụng HTL: \(AB^2=BH.BC;AC^2=CH.BC\)
\(\Leftrightarrow\dfrac{AB^2}{AC^2}=\dfrac{BH.BC}{CH.BC}=\dfrac{BH}{CH}\)
Đúng 1
Bình luận (0)
Câu 7: Cho tam giác ABC vuông tại A, biết AB=3cm, AC=4cm, kẻ đường cao AH
a. Tính BC, AH
b. Kẻ HM ⊥ AB, HN ⊥ AC. Chứng minh AM.AB=AN.AC
a) Xét tam giác ABC vuông tại A:
\(BC^2=AB^2+AC^2\left(Pytago\right)\)
\(\Rightarrow BC=\sqrt{AB^2+AC^2}=\sqrt{3^2+4^2}=5\left(cm\right)\)
Áp dụng HTL trong tam giác ABC vuông tại A có đường cao AH:
\(AH.BC=AB.AC\Rightarrow AH=\dfrac{AB.AC}{BC}=\dfrac{3.4}{5}=2,4\left(cm\right)\)
b) Áp dụng HTL trong tam giác ABH vuông tại H và tam giác AHC vuông tại H:
\(\left\{{}\begin{matrix}AM.AB=AH^2\\AN.AC=AH^2\end{matrix}\right.\)\(\Rightarrowđpcm\)
Đúng 1
Bình luận (0)
b: Xét ΔAHB vuông tại H có HM là đường cao
nên \(AM\cdot AB=AH^2\left(1\right)\)
Xét ΔAHC vuông tại H có HN là đường cao
nên \(AN\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AM\cdot AB=AN\cdot AC\)
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A có AB =6cm, bc = 10cm đường cao ah
a) chứng minh ah^2=bh.ch
ΔACB vuông tại A
mà AH là đường cao
nên AH^2=HB*HC
Đúng 1
Bình luận (0)
Bài 1: Cho tam giác ABC vuông tại A, AB = 6cm, AC = 8cm. Kẻ đường cao AH
a) Giải tam giác vuông ABC (góc làm tròn đến phút).
b) Gọi G, K là hình chiếu của H lần lượt lên AB và AC. Chứng minh rằng: AG.AB=AK.AC
Bài 2: Cho vuông tại A, đường cao AH có , đường cao AH có HB=9cm,HC=16cm
a) Tính AB, AC và AH.
b) Hạ HD vuông góc AB,HE vuông góc AC . Tính chu vi và diện tích tứ giác ADHE.
Bài 1:
a: ΔABC vuông tại A
=>\(BC^2=AB^2+AC^2\)
=>\(BC^2=6^2+8^2=100\)
=>BC=10(cm)
Xét ΔABC vuông tại A có \(sinC=\dfrac{AB}{BC}=\dfrac{3}{5}\)
nên \(\widehat{C}\simeq37^0\)
=>\(\widehat{B}=90^0-37^0=53^0\)
b: Xét ΔHAB vuông tại H có HG là đường cao
nên \(AG\cdot AB=AH^2\left(1\right)\)
Xét ΔAHC vuông tại H có HK là đường cao
nên \(AK\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AG\cdot AB=AK\cdot AC\)
Đúng 2
Bình luận (1)
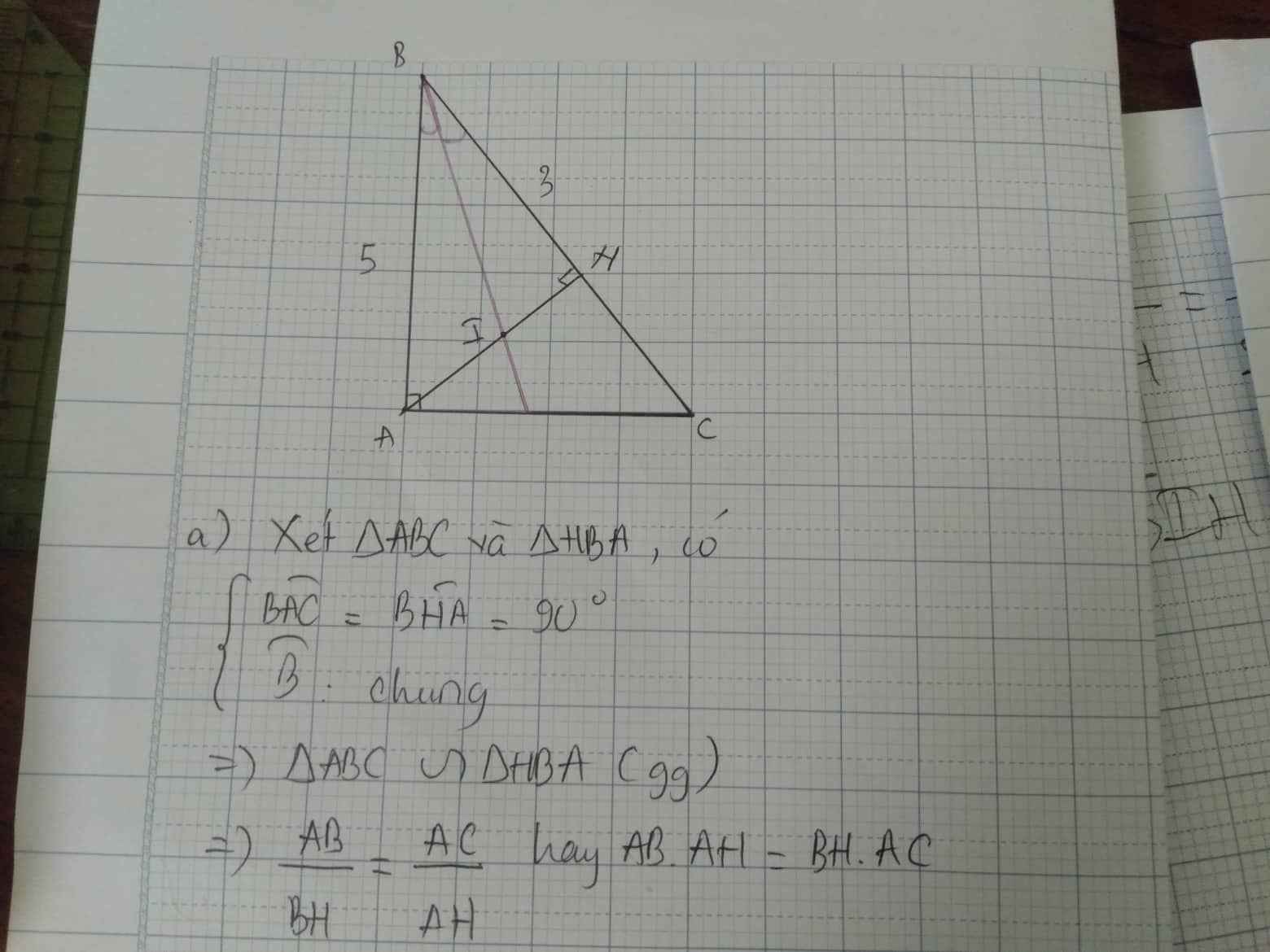
Cho tam giác ABC vuông tại A, đường cao AH
a) CM: tam giác ABC đồng dạng tam giác HBA, từ đó suy ra: AB.AH = BH.AC
b) Tia phân giác góc ABC cắt AH tại I (i). Biết BH=3cm; AB=5cm. Tính AI (ai), IH (ih)
c) Tính diện tích tam giác AHB
Cho tam giác ABC vuông tại A, AB=12cm, AC=16cm, vẽ đường cao AH
a)CM:tam giác HAC đồng dạng với tam giác ABC
b)Tính BC và HC
a, Xét tam giác HAC và tam giác ABC
^C _ chung
^AHC = ^BAC = 900
Vậy tam giác HAC ~ tam giác ABC (g.g)
=> HC/AC=AC/BC ( cạnh tương ứng tỉ lệ )
=> AC^2 = HC . BC
b, Theo định lí Pytago tam giác ABC vuông tại A
\(BC=\sqrt{AB^2+AC^2}=20cm\)
Ta có AC^2 = HC . BC (cmt)
Thay vào ta được \(16^2=HC.20\Rightarrow HC=\dfrac{16^2}{20}=\dfrac{64}{5}cm\)
Đúng 2
Bình luận (0)
a. xét tam giác vuông HAC và tam giác vuông ABC, có:
góc C: chung
Vậy tam giác vuông HAC đồng dạng tam giác vuông ABC
b. Áp dụng định lí pitago vào tam giác vuông ABC
\(BC^2=AB^2+AC^2\)
\(\Rightarrow BC=\sqrt{12^2+16^2}=\sqrt{400}=20cm\)
ta có: tam giác HAC đồng dạng tam giác ABC
\(\Rightarrow\dfrac{HC}{AC}=\dfrac{AC}{BC}\)
\(\Leftrightarrow HC.BC=AC^2\)
\(\Leftrightarrow20HC=16^2\)
\(\Leftrightarrow20HC=256\)
\(\Leftrightarrow HC=\dfrac{64}{5}cm\)
Đúng 1
Bình luận (2)
Cho Tam giác ABC vuông tại A ( AB < AC ) có đường cao AH
a) Chứng minh: tam giác ABC đồng dạng tam giác CBA
b) Chứng minh: AH^2 = BH . HC
c) Trên đường thẳng vuông góc AC tại C , lấy điểm D sao cho CD = AB (D và B nằm khác phía sao với đường thẳng AC) . Đoạn thẳng HD cắt đoạn thẳng AC tại S . Kẻ AF vuông góc HS tại F .
Chứng minh: BH . CH = HF.HD
d) Chứng minh: góc SCF = góc SHC
a: Sửa đề: ΔABH đồng dạng với ΔCBA
Xét ΔABH vuông tại H và ΔCBA vuông tại A có
góc B chung
=>ΔABH đồng dạng với ΔCBA
b: Xét ΔAHB vuông tại H và ΔCHA vuông tại H có
góc HAB=góc HCA
=>ΔAHB đồng dạng với ΔCHA
=>HA/HC=HB/HA
=>HA^2=HB*HC
c: Xét tứ giác ABCD có
AB//CD
AB=CD
=>ABCD là hbh
=>AD//BC
=>AD vuông góc AH
ΔADH vuông tại A có AF là đường cao
nên HF*HD=HA^2=HB*HC
Đúng 0
Bình luận (0)