Tam giác ABC có \(\widehat{A}=20^0,\widehat{B}=30^0;AB=60cm\). Đường vuông góc kẻ từ C đến AB cắt AB tại P (h.33)
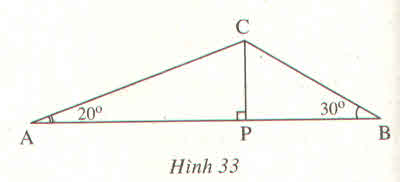
Hãy tìm :
a) AP, BP
b) CP
Cho tam giác ABC có \(\widehat{B}=80^0,\widehat{C}=30^0\). Tia phân giác của góc A cắt BC ở D. Tính \(\widehat{ADC},\widehat{ADB}\) ?
\(\widehat{BAC}\)= 1800 - (\(\widehat{B}+\widehat{C}\)) = 1800 - ( 800 + 300)= 700
\(\widehat{A}_1\)=\(\widehat{A}_2\)=\(\dfrac{\widehat{A}}{2}\)=\(\dfrac{70^0}{2}\)= 350
\(\widehat{ADC}=\widehat{B}+\widehat{A}_1\)(Góc ngoài của tam giác)
=800 + 350)= 1150
Do đó \(\widehat{ADB}\)= 1800 - \(\widehat{ADC}\)= 1800 + 1150=650
Hình vẽ: 

Gọi A1, A2 là 2 góc được tạo ra bởi tia phân giác góc A.
Ta có:
Góc ∠BAC = 1800 – ( ∠B + ∠C)
= 1800 – ( 800 + 300) = 700
Hay ta có thể gọi ∠A = 700
Góc ∠A1 = ∠A2
= ∠A/2 = 700 /2 = 350
Xét tam giác ADC ta có: Góc ∠ADC = 1800 – (∠C + ∠A2)= 1800 – (350 + 300)= 1150
Do đó góc ∠ADB = 1800 – ∠ADC= 1800 – 1150
= 650
Giải:
ˆBACBAC^= 1800 - (ˆBB^+ˆCC^) = 1800 - ( 800 + 300)= 700
ˆA1A1^=ˆA2A2^=ˆA2A^2=70027002= 350
ˆADCADC^=ˆBB^+ˆA1A1^(Góc ngoài của tam giác)
=800 + 350)= 1150
Do đó ˆADBADB^= 1800 - ˆADCADC^= 1800 + 1150=650
a) cho tam giác ABC có \(\widehat{B}=40^0,\widehat{C}=30^0\). dựng điểm D khác phía với B sao cho \(\widehat{DAC}=\widehat{DCA}=50^0\)
Chứng minh rằng tam giác ABC cân.
b) chứng minh rằng chu vi một tam giác có các góc nhọn hơn 4 lần bán kính đường tròn ngoại tiếp tam giác.
câu a) mình nghĩ chứng minh ABD cân chứ ạ, sao lại ABC

Gọi H là trung điểm của AC. \(\Delta\)DAC cân tại D.
Do đó DH\(\perp\)AC và AH = \(\frac{1}{2}\)AC (1)
Vẽ AK \(\perp\)BC. Vì \(\Delta\)AKC vuông tại K và ^BCA = 300
nên AK = \(\frac{1}{2}\)AC (2)
Từ (1) và (2) suy ra AK = AH
Xét \(\Delta\)AKB và \(\Delta\)AHD có:
^AKB = ^AHD (=900)
AK = AH(gt)
^BAK = ^DAH (=500)
Do đó \(\Delta\)AKB = \(\Delta\)AHD (g.c.g)
=> AB = AD
Vậy \(\Delta\)ABD cân tại A(đpcm)
Cho tam giác ABC có \(\widehat{B}=\widehat{C}=50^0.\) Gọi K là điểm trong tam giác sao cho \(\widehat{KBC}=10^0,\widehat{KCB=30^0.}\) CMR: tam giác ABK là tam giác cân và tính \(\widehat{BAK}\)
Cho tam giác ABC có \(\widehat{A}=100^0;\widehat{B}-\widehat{C}=20^0\).
Tính \(\widehat{B}\) và \(\widehat{C}\) ?
\(\widehat{A}=100^0\)
\(\Rightarrow\widehat{B}+\widehat{C}=180^0-100^0=80^0\)
Mà \(\widehat{B}-\widehat{C}=20^0\)
\(\Rightarrow\widehat{B}=\left(180^0+20^0\right):2=100^0\); \(\widehat{C}=\left(180^0-20^0\right):2=80^0\)
Áp dụng định lý tổng ba góc của 1 tam giác bằng 180\(^o\), ta có:
\(\widehat{A}+\widehat{B}+\widehat{C}=180^0\)
\(100^0+\widehat{B}+\widehat{C}=180^0\)
\(\widehat{B}+\widehat{C}=180^0-100^0\)
\(\widehat{B}+\widehat{C}=80^0\)
Mà \(\widehat{B}-\widehat{C}=20^0\left(gt\right)\)
\(\Rightarrow\widehat{B}=\left(80^0+20^0\right)\div2=50^0\)
\(\widehat{C}=50^0-20^0=30^0\)
Vậy \(\widehat{B}=50^0;\widehat{C}=30^0\)
Áp dụng định lý tổng ba góc của một tam giác, ta có:
\(\widehat{A}\) + \(\widehat{B}\)+ \(\widehat{C}\) = 1800
hay 1000 + \(\widehat{B}\) + \(\widehat{C}\) = 1800
\(\Rightarrow\)\(\widehat{B}\)+ \(\widehat{C}\) = 1800 - 1000 = 800
\(\widehat{B}\) = (800 + 200) : 2 = 500
\(\widehat{C}\) = 800 - 500 = 300
Vậy \(\widehat{B}\) = 500 và
CHo tam giác ABC \(\widehat{A}=90^0\)\(\widehat{B}=20^0\). Lấy E,F thuộc AC,AB sao cho \(\widehat{ABE}=10^0\),\(\widehat{ACF}=30^0\)
\(T\text{ính}\widehat{CFE}\)
cho \(\Delta ABC\) có \(\widehat A={40^0}\) biết \(\widehat B= 3\widehat C\) tam giác abc là tam giác gì
giúp mik với
\(\widehat{B}+\widehat{C}=140^0\)
\(\Leftrightarrow4\cdot\widehat{C}=140^0\)
\(\Leftrightarrow\widehat{C}=35^0\)
hay \(\widehat{B}=105^0\)
Vậy: ΔABC tù
Cho tam giác ABC có \(\widehat{B}-\widehat{C}=20^0\). Tia phân giác của góc A cắt BC ở D.
Tính số đo các góc \(\widehat{ADC},\widehat{ADB}\) ?
Ta có :
A+B+C=180(tính chất của một tam giác)
⇒A=180-B-C
⇒A=180-20
⇒A=160
vì tia phân giác của góc A cắt BC tại D nên A1=A2=\(\dfrac{160}{2}\)=80
\(\Leftrightarrow\)D1=80
Vì góc D1 và góc D2 là 2 góc kề bù nên D1+D2=180
mà góc D1=80
\(\Rightarrow\)D2=180-80
\(\Rightarrow\)D2=100
Vay : D1=80, D2=100
mk ko viết đc kí hiệu góc và độ mong mọi người thông cảm![]()
Cho tam giác ABC có: \(\widehat{BAC}=15^0;\widehat{ABC}=30^0\). Gọi M là trung điểm AB. Tính \(\widehat{ACM}\)?
Cho tam giác ABC vuông tại A, biết \(\widehat{B}=4\widehat{C}\). Tìm số đo của góc B
\(A.\widehat{B}=72^0\) \(B.\widehat{B}=18^0\) \(C.\widehat{B}=48^0\) \(D.\widehat{B}=64^0\)
Cho \(\Delta ABC;\widehat{A}=30^0;\widehat{B}=70^0;\widehat{C}=80^0.\) AH là đường cao, P thuộc AC, Q thuộc AB. Xác định vị trí tam giác HPQ để chu vi tam giác HPQ có giá trị nhỏ nhất.
( Mong mọi người giúp mình nhé. xin trân trọng cảm ơn )
wwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwww