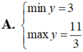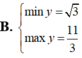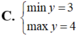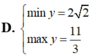Câu 1: Tìm GTLN và GTNN của hàm số: y= ex + 2x -3ln(x + 1) , \(x\in[1;3]\)
Câu 2: Giải phương trình và bất phương trình sau:
a) \(log_{\sqrt{3}}(x-4)=1+log_3\left(x-2\right)\)
b) \(4^x-3.2^{x+1}+5\ge0\)
Tìm GTLN (max); GTNN (min) của hàm số y = 2 x + 1 + 4 - x .
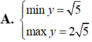
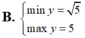
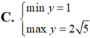
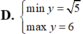
Cho \(x\ge-1\) . Tìm GTLN và GTNN của hàm số \(y=\dfrac{x+1}{\sqrt{x^2+1}}\)
Do \(\left\{{}\begin{matrix}x\ge-1\Rightarrow x+1\ge0\\\sqrt{x^2+1}>0\end{matrix}\right.\) \(\Rightarrow y\ge0\)
\(y_{min}=0\) khi \(x=-1\)
Lại có: \(y^2=\dfrac{\left(x+1\right)^2}{x^2+1}=\dfrac{x^2+2x+1}{x^2+1}=\dfrac{2\left(x^2+1\right)-x^2+2x-1}{x^2+1}=2-\dfrac{\left(x-1\right)^2}{x^2+1}\le2\)
\(\Rightarrow y\le\sqrt{2}\)
\(y_{max}=\sqrt{2}\) khi \(x=1\)
Tìm GTLN và GTNN của hàm số : 1. y = sinx + 2cosx +1 / 2sinx + cosx + 3
2.y= 2sin^2sinx - 3 sinx cosx + cos^2 x
Giải phương trình : 1. 2sin^2 * 2x + sin7x -1 = sinx
2.cos 4x + 12 sin^2 x -1 = 0
Tìm GTLN và GTNN của các hàm số sau: y = x 2 + x + 1 x 2 - 2 + 1 là:
A. m a x y = 3 m i n y = 1 3
B. m a x y = 3 m i n y = - 1 3
C. m a x y = 1 m i n y = 1 3
D. m a x y = 3 m i n y = 1
tìm gtln gtnn của hàm số
\(y=\sqrt{1+x}+\sqrt{1-x}+\dfrac{x^2}{4}\)
Lời giải:
TXĐ: $[-1;1]$
$y'=\frac{1}{2\sqrt{x+1}}-\frac{1}{2\sqrt{1-x}}+\frac{x}{2}$
$y'=0\Leftrightarrow x=0$
$f(0)=2$;
$f(1)=f(-1)=\sqrt{2}+\frac{1}{4}$
Vậy $f_{\min}=2; f_{\max}=\frac{1}{4}+\sqrt{2}$
Tìm GTLN, GTNN của hàm số:
\(y=\sqrt{5sin^2x+1}+\sqrt{5cos^2x+1}\)
Đặt \(\left\{{}\begin{matrix}\sqrt{5sin^2x+1}=a\\\sqrt{5cos^2x+1}=b\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}1\le a;b\le\sqrt{6}\\a^2+b^2=5\left(sin^2x+cos^2x\right)+2=7\end{matrix}\right.\)
\(y=a+b\le\sqrt{2\left(a^2+b^2\right)}=\sqrt{14}\)
\(y_{max}=\sqrt{14}\) khi \(cos2x=0\Rightarrow x=\dfrac{\pi}{4}+\dfrac{k\pi}{2}\)
Do \(1\le a\le\sqrt{6}\Rightarrow\left(a-1\right)\left(a-\sqrt{6}\right)\le0\)
\(\Rightarrow a\ge\dfrac{a^2+\sqrt[]{6}}{\sqrt{6}+1}\)
Tương tự ta có \(b\ge\dfrac{b^2+\sqrt{6}}{\sqrt{6}+1}\)
\(\Rightarrow y=a+b\ge\dfrac{a^2+b^2+2\sqrt{6}}{\sqrt{6}+1}=\dfrac{7+2\sqrt{6}}{\sqrt{6}+1}=\sqrt{6}+1\)
\(y_{min}=\sqrt{6}+1\) khi \(sin2x=0\Rightarrow x=\dfrac{k\pi}{2}\)
Tìm GTLN và GTNN của hàm số y= 4x2 - 2|2x-1| - 4x - 5 (-2 < hoặc = x < hoặc = 1)
\(4x^2-2\left|2x-1\right|-4x-5=\left(2x-1\right)^2-2\left|2x-1\right|+1-5\)
\(=\left(\left|2x-1\right|-1\right)^2-5\ge-5\)
Dấu "=" xảy ra khi \(\left|2x-1\right|=1\Leftrightarrow x=1\text{ hoặc }x=0\)
=> GTNN của y là -5
\(y=\left(\left|2x-1\right|-1\right)^2-5\)
\(-2\le x\le1\Rightarrow-5\le2x-1\le1\Rightarrow0\le\left|2x-1\right|\le5\)
\(\Rightarrow-1\le\left|2x-1\right|-1\le4\Rightarrow0\le\left(\left|2x-1\right|-1\right)^2\le16\)
\(\Rightarrow y\le16-5=11\)
Dấu "=" xảy ra khi x = -2
Vậy GTLN của y là 11.
Tìm GTLN (max), GTNN (min) của hàm số y = x + 2 x với x ∈ 1 ; 3