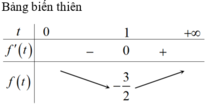
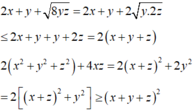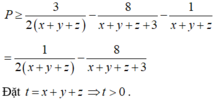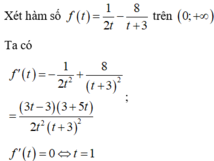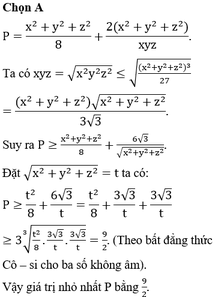Cho x,y,z là ba số thực dương thuộc đoạn [1;2] thỏa mãn điều kiện \(a^2+b^2+c^2=6\). CMR \(a+b+c\text{ ≥}0\)
IH
Những câu hỏi liên quan
Cho x,y,z là ba số thực dương thỏa:x+y+z=3 .Tìm GTNN của biểu thức Q=x+1/1+y^2 +y+1/1+z^2 +z+1/1+x^2
hây ya bài này làm chán thấy m3 luôn đó
Đúng 0
Bình luận (0)
\(\frac{x+1}{y^2+1}=x+1-\frac{xy^2+y^2}{y^2+1}\ge x+1-\frac{xy^2+y^2}{2y}=x+1-\frac{xy+y}{2}\)
tiếp đó bạn dùng BĐT \(\text{xy+yz+xz}\le\frac{\left(x+y+z\right)^2}{3}\)
Đúng 0
Bình luận (0)
Cho ba số x, y, z thuộc Z biết 1 số 0, 1 số dương, 1 số âm và thỏa đẳng thức: x2=y4(y-z)
1/ x hoặc y có thể bằng 0 được ko?
2/Tìm xem số nào là 0, số nào là dương, số nào là âm
giả sử x = 0
=) ta có : 0 = y4 ( y - z )
vô lí vì y4 ( y - z ) lớn hơn hoặc bé hơn 0
giả sử y = 0
=) ta có : x2 = 0 ( 0 - z ) = 0 ( vô lí )
vô lí vì x2 lớn hơn 0
=) x và y không thể = 0
1. Giả sử x=0 => y\(\ne\)0
=>x^2=0^2=0 => y^4(y-z)=0 => vì y khác 0 nên y-z=0 => y=z (loại)
giả xử y=0 =>x khác 0
=>y^4=0 =>y^4(y-z)=0 hay x^2=0 =>x=0 (loại)
Vậy x hoặc y ko thể =0
2. Từ câu 1=> z=0 =>x^2=y^5 => giả sử y âm =>y^5 âm , mà x^2 luôn dương => (loại)
vậy x âm y dương z=0
vì x và y không thể = 0 =) z = 0
=) ta có : x2=y4(y-0)
= x2=y5
xét : x2 nếu x là số dương thì x \(\ge\)0 ( Đ )
nếu x là âm thì x cũng \(\ge\)0 ( C )
xét y5 nếu y là âm =) y5\(\le\) 0 ( M )
nếu y là dương =) y5\(\ge\)0 ( :] )
Qua ( Đ ) , ( C ) , ( M ) , ( :] ) =) x \(\le\)0 và y\(\ge\)0
vậy : .......................................
không chắc lắm
Cho x, y, z là ba số thực dương và đạt giá trị nhỏ nhất. Tính
x
+
y
+
z
. A.
3
B.
3
3
C.
1
D.
3
2
Đọc tiếp
Cho x, y, z là ba số thực dương và 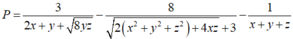 đạt giá trị nhỏ nhất. Tính
x
+
y
+
z
.
đạt giá trị nhỏ nhất. Tính
x
+
y
+
z
.
A. 3
B. 3 3
C. 1
D. 3 2
Cho ba số thực dương x,y,z thỏa mãn x+y+z = 2. Tìm GTNN của biểu thức:
\(P=\dfrac{1}{xy}+\dfrac{1}{yz}\)
\(P=\dfrac{1}{y}\left(\dfrac{1}{x}+\dfrac{1}{z}\right)\ge\dfrac{1}{y}.\dfrac{4}{x+z}=\dfrac{4}{y\left(x+z\right)}\ge\dfrac{4}{\dfrac{\left(y+x+z\right)^2}{4}}=4\)
\(P_{min}=4\) khi \(\left(x;y;z\right)=\left(\dfrac{1}{2};1;\dfrac{1}{2}\right)\)
Đúng 1
Bình luận (2)
Cho ba số thực dương x,y,z. Tính GTNN \(P=\dfrac{1}{2}\left(x^2+y^2+z^2\right)+\dfrac{x}{yz}+\dfrac{y}{zx}+\dfrac{z}{xy}\)
Ta có:
\(\dfrac{x}{yz}+\dfrac{y}{zx}+\dfrac{z}{xy}=\dfrac{1}{2}\left(\dfrac{x}{yz}+\dfrac{y}{zx}+\dfrac{x}{yz}+\dfrac{z}{xy}+\dfrac{y}{zx}+\dfrac{z}{xy}\right)\ge\dfrac{1}{2}\left(\dfrac{2}{z}+\dfrac{2}{y}+\dfrac{2}{x}\right)\)
\(\Rightarrow P\ge\dfrac{1}{2}\left(x^2+y^2+z^2\right)+\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}\)
\(\Rightarrow P\ge\dfrac{1}{2}\left(x^2+\dfrac{1}{x}+\dfrac{1}{x}\right)+\dfrac{1}{2}\left(y^2+\dfrac{1}{y}+\dfrac{1}{y}\right)+\dfrac{1}{2}\left(z^2+\dfrac{1}{z}+\dfrac{1}{z}\right)\)
\(\Rightarrow P\ge\dfrac{3}{2}\sqrt[3]{\dfrac{x^2}{x^2}}+\dfrac{3}{2}\sqrt[3]{\dfrac{y^2}{y^2}}+\dfrac{3}{2}\sqrt[3]{\dfrac{z^2}{z^2}}=\dfrac{9}{2}\)
Dấu "=" xảy ra khi \(x=y=z=1\)
Đúng 1
Bình luận (0)
cho ba số x,y,z là ba số dương thoả mãn x+y+z=1
cm 1/x+1/y+1/z>=9
Cho x,y,z là ba số thực dương thay đổi. Tìm giá trị nhỏ nhất của biểu thức P
x
(
x
8
+
2
yz
)
+
y
(
y
8
+
2
xz
)
+
z
(
z
8
+
2
xy
)
. A. 9/2...
Đọc tiếp
Cho x,y,z là ba số thực dương thay đổi. Tìm giá trị nhỏ nhất của biểu thức P= x ( x 8 + 2 yz ) + y ( y 8 + 2 xz ) + z ( z 8 + 2 xy ) .
A. 9/2.
B. 9/4.
C.9.
D. 6.
Cho x,y,z là ba số thực dương thỏa mãn điều kiện \(\left(x-z\right)\left(y-z\right)=z^2\).Chứng minh rằng tích xyz là số chính phương
cho x,y,z là ba số thực dương thỏa mãn: x+y+z=3.tìm GTNN của biểu thức:Q=\(x+1\over1+y^2 \)+\(y+1\over1+z^2\)+\(z+1\over1+x^2\)