trong mp Oxy cho tam giác ABC . gọi E(7;1) và F(11/5;13/5) lần lượt là chân đường cao hạ từ B , C biết BC có pt X+3y-4=0.B có hoàn độ dương,Tìm A
QV
Những câu hỏi liên quan
Trong mp tọa độ Oxy, cho A(3;0), B(2;4). Gọi D là chân đường phân giác trong góc O của tam giác ABC. Tìm tọa độ của D.
Trong mp toạ độ oxy, cho tam giác ABC vuông tại A, BC có pt là y=0, M là trung điểm cạnh BC, điểm E thuộc đoạn MC. Gọi O(2;1/2) và I(7;8) lần lượt là tâm đường tròn ngoịa tiếp tam giác ABE và ACE. Tìm toạ độ E,M biết rằng hoành độ điểm E lớn hơn hoành độ điểm M
trong mp oxy cho tam giac ABC vuông tại A có 4AB=3AC. Gọi E(0;-2) là chân đường phân giác trong góc ABC, biết phương trình BC : 3x+4y-7=0. Tìm tọa độ điểm A
Đặt \(AB=3x\Rightarrow AC=4x\Rightarrow BC=\sqrt{9x^2+16x^2}=5x\)
Theo tính chất phân giác: \(\frac{AE}{AB}=\frac{CE}{BC}\Rightarrow\frac{AE}{3x}=\frac{CE}{5x}\Rightarrow AE=\frac{3}{5}CE\)
\(\Rightarrow CE+\frac{3}{5}CE=4x\Rightarrow CE=\frac{5}{2}x\)
Gọi H là hình chiếu của E lên BC \(\Rightarrow EH\) nhận \(\overrightarrow{n_{EH}}=\left(4;-3\right)\) là 1 vtpt
Phương trình EH: \(4x-3y-6=0\)
Toạ độ H là nghiệm: \(\left\{{}\begin{matrix}3x+4y-7=0\\4x-3y-6=0\end{matrix}\right.\) \(\Rightarrow H\left(\frac{9}{5};\frac{2}{5}\right)\)
Do \(\Delta CHE\sim\Delta CAB\Rightarrow\frac{CH}{CA}=\frac{CE}{BC}\Rightarrow CH=\frac{CE.AC}{BC}=\frac{\frac{5}{2}x.4x}{5x}=2x\)
\(\Rightarrow CH=\frac{2}{3}HB\Rightarrow\overrightarrow{CH}=\frac{2}{3}\overrightarrow{HB}\)
Gọi \(C\left(c;\frac{7-3c}{4}\right)\); do \(\left\{{}\begin{matrix}\overrightarrow{EA}=\frac{3}{5}\overrightarrow{CE}\\\overrightarrow{CH}=\frac{2}{3}\overrightarrow{HB}\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}A\left(-\frac{3}{5}c;\frac{9c-85}{20}\right)\\B\left(\frac{9-3c}{2};\frac{-43+45c}{40}\right)\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AB}=\left(\frac{45-9c}{10};\frac{27c-127}{40}\right)\\\overrightarrow{AC}=\left(\frac{8c}{5};\frac{60-9c}{10}\right)\end{matrix}\right.\)
\(AB\perp AC\Rightarrow\overrightarrow{AB}.\overrightarrow{AC}=0\Rightarrow\frac{8c\left(45-9c\right)}{50}+\frac{\left(27c-127\right)\left(60-9c\right)}{400}=0\)
Giải pt này sẽ xong bài toán, xấu quá :(
Đúng 0
Bình luận (1)
Trong mp tọa độ Oxy cho tam giác ABC có A(1;0).B(-1;1),C(5;-1). Tọa độ trực tâm H của tam giác ABC là
Giả sử trực tâm của tam giác ABC có tọa độ \(H\left(x;y\right)\)
\(\left\{{}\begin{matrix}\overrightarrow{BC}=\left(6;-2\right)\\\overrightarrow{AH}=\left(x-1;y\right)\end{matrix}\right.\Rightarrow\overrightarrow{BC}\perp\overrightarrow{AH}\Leftrightarrow\overrightarrow{AH}.\overrightarrow{BC}=0\)
\(\Leftrightarrow6\left(x-1\right)-2y=0\)
\(\Leftrightarrow3x-y=3\left(1\right)\)
Lại có:
\(\left\{{}\begin{matrix}\overrightarrow{AB}=\left(-2;1\right)\\\overrightarrow{CH}=\left(x-5;y+1\right)\end{matrix}\right.\Rightarrow\overrightarrow{AB}\perp\overrightarrow{CH}\Leftrightarrow\overrightarrow{CH}.\overrightarrow{AB}=0\)
\(\Leftrightarrow-2\left(x-5\right)+y+1=0\)
\(\Leftrightarrow-2x+y=-11\left(2\right)\)
\(\left(1\right);\left(2\right)\Rightarrow\left\{{}\begin{matrix}x=-8\\y=-27\end{matrix}\right.\Rightarrow H\left(-8;-27\right)\)
Đúng 3
Bình luận (1)
a) Cho hbh ABCD. Gọi M là trung điểm CD; N là điểm thuộc AD sao cho 3ANAD. Gọi G là trọng tâm tam giác BMN, đường thẳng AG cắt BC tại K. Tính tỉ số dfrac{BK}{BC}b) Trong mp tọa độ Oxy, cho tam giác ABC cân tại C và có diện tích bằng 10. Đường thẳng AB có pt x-2y0. Điểm I(4;2) là trung điểm AB, điểm Mleft(4;dfrac{9}{2}right) thuộc đường thẳng BC. Tìm tọa độ A,B,C biết B có tung độ là số nguyên
Đọc tiếp
a) Cho hbh ABCD. Gọi M là trung điểm CD; N là điểm thuộc AD sao cho 3AN=AD. Gọi G là trọng tâm tam giác BMN, đường thẳng AG cắt BC tại K. Tính tỉ số \(\dfrac{BK}{BC}\)
b) Trong mp tọa độ Oxy, cho tam giác ABC cân tại C và có diện tích bằng 10. Đường thẳng AB có pt x-2y=0. Điểm I(4;2) là trung điểm AB, điểm \(M\left(4;\dfrac{9}{2}\right)\) thuộc đường thẳng BC. Tìm tọa độ A,B,C biết B có tung độ là số nguyên
Trong mp hệ tọa độ oxy cho tam giác ABC có trực tâm H(3,0) và trung điểm của BC là điểm I(6,1). Đường thẳng AH có phương trình x+2y-3=0. Gọi D và E lần lượt là chân đường cao kẻ từ B và C của tam giác ABC. Xác định tọa độ biết rằng đường thẳng DẺ có pt: x-2=0 và D có tung độ dương
Trong mp tọa độ oxy, cho A(2;3),B(-1,-1),C(6,0)
tìm tọa độ trực tam của tam giác ABC
Giải giúp mik với
Trong mp Oxy cho A(-2;8)B(-6;1) C(0;4). Tam giác ABC là
A tam giác cân
B tam giác vuông
C tam giác vuông cân
D tam giác đều
Xem chi tiết
\(\overrightarrow{AC}=\left(2;-4\right);\overrightarrow{BC}=\left(6;3\right)\)
Vì 2.6+(-4).3=0 => AC_|_BC => tg ABC là tam giác vuông
Đúng 2
Bình luận (0)
Trong mặt phẳng với hệ trục Oxy, cho tam giác ABC vuông tại C, có phân giác AD với Dleft(dfrac{7}{2};-dfrac{7}{2}right) thuộc BC. Gọi E, F lần lượt thuộc các cạnh AB, AC sao cho AEAF. Đường thẳng EF cắt BC tại K. Biết Eleft(dfrac{3}{2};-dfrac{5}{2}right), F có hoành độ nhỏ hơn 3 và phương trình đường thẳng AK là x-2y-30. Viết phương trình các cạnh tam giác ABC.
Đọc tiếp
Trong mặt phẳng với hệ trục Oxy, cho tam giác ABC vuông tại C, có phân giác AD với \(D\left(\dfrac{7}{2};-\dfrac{7}{2}\right)\) thuộc BC. Gọi E, F lần lượt thuộc các cạnh AB, AC sao cho \(AE=AF\). Đường thẳng EF cắt BC tại K. Biết E\(\left(\dfrac{3}{2};-\dfrac{5}{2}\right)\), F có hoành độ nhỏ hơn 3 và phương trình đường thẳng \(AK\) là \(x-2y-3=0\). Viết phương trình các cạnh tam giác ABC.
Từ hình vẽ thì hướng giải như sau:
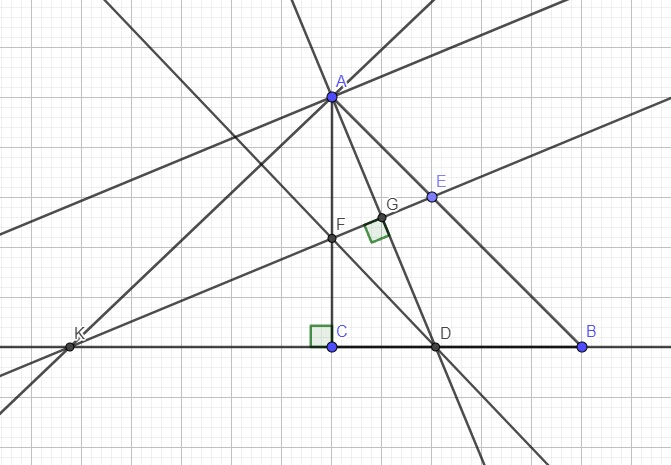
Dễ dàng nhận ra \(DF\perp AK\), từ đó biết vtpt của DF \(\Rightarrow\) phương trình DF
\(\Rightarrow\) Tọa độ F (là giao của DF và đường tròn tâm D bán kính DE do DE=DF)
Biết tọa độ F \(\Rightarrow\) viết được pt AD qua D vuông góc EF
\(\Rightarrow\) Tọa độ A từ là giao AK và AD
\(\Rightarrow\) Phương trình AB qua A và E, phương trình AC qua A và F, phương trình BC qua D và vuông góc AF
Đúng 3
Bình luận (0)
Trong mp tọa độ oxy, cho A(1;0),B(-1,-1),C(5;-1)
tìm tọa độ trực tam H của tam giác ABC
Gọi K là hình chiếu của A lên BC, I là hình chiếu của B lên AC
\(\Rightarrow\left\{{}\begin{matrix}AK\perp BC\\BI\perp AC\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AK}.\overrightarrow{BC}=\overrightarrow{0}\\\overrightarrow{BI}.\overrightarrow{AC}=\overrightarrow{0}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left(x_K-x_A\right)\left(x_C-x_B\right)=0\\\left(y_K-y_A\right)\left(y_C-y_B\right)=0\\\left(x_I-x_B\right)\left(x_C-x_A\right)=0\\\left(y_I-y_B\right)\left(y_C-y_A\right)=0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}I\left(...\right)\\K\left(....\right)\end{matrix}\right.\)
Viết phương trình đường thẳng ua A và K; Viết phương trìn đường thẳng ua B và I.
Giao điểm của 2 đường thẳng đó chính là tọa độ trực tâm H
Đúng 2
Bình luận (4)







