Tính khoảng cách từ điểm \(A\left(1;0;1\right)\) đến đường thẳng \(\Delta:\dfrac{x-1}{2}=\dfrac{y}{2}=\dfrac{z}{1}\)
SK
Những câu hỏi liên quan
Cho hình chóp \(S.ABCD\) với đáy \(ABCD\) là hình vuông cạnh \(a\). Cho biết \(SA = a\) và \(SA\) vuông góc với \(\left( {ABCD} \right)\).
a) Tính khoảng cách từ điểm \(B\) đến \(\left( {SAD} \right)\).
b) Tính khoảng cách từ điểm \(A\) đến cạnh \(SC\).
a) Ta có:
\(\begin{array}{l}\left. \begin{array}{l}SA \bot \left( {ABCD} \right) \Rightarrow SA \bot AB\\AB \bot A{\rm{D}}\end{array} \right\} \Rightarrow AB \bot \left( {SA{\rm{D}}} \right)\\ \Rightarrow d\left( {B,\left( {SA{\rm{D}}} \right)} \right) = AB = a\end{array}\)
b) Kẻ \(AH \bot SC \Rightarrow d\left( {A,SC} \right) = AH\)
Tam giác \(ABC\) vuông tại \(B\)\( \Rightarrow AC = \sqrt {A{B^2} + B{C^2}} = a\sqrt 2 \)
Tam giác \(SAC\) vuông tại \(A\)\( \Rightarrow SC = \sqrt {S{A^2} + A{C^2}} = a\sqrt 3 \)
Tam giác \(SAC\) vuông tại \(A\) có đường cao \(AH\)\( \Rightarrow AH = \frac{{SA.AC}}{{SC}} = \frac{{a\sqrt 6 }}{3}\)
Vậy \(d\left( {A,SC} \right) = \frac{{a\sqrt 6 }}{3}\).
Đúng 0
Bình luận (0)
Cho hình chóp \(S.ABCD\) có \(SA \bot \left( {ABCD} \right)\), đáy \(ABCD\) là hình vuông cạnh \(a\), \(SA = a\) (Hình 78).
a) Tính khoảng cách từ điểm \(S\) đến đường thẳng \(C{\rm{D}}\).
b) Tính khoảng cách từ điểm \(D\) đến mặt phẳng \(\left( {SAB} \right)\).
c) Tính khoảng cách từ điểm \(A\) đến mặt phẳng \(\left( {SCD} \right)\).
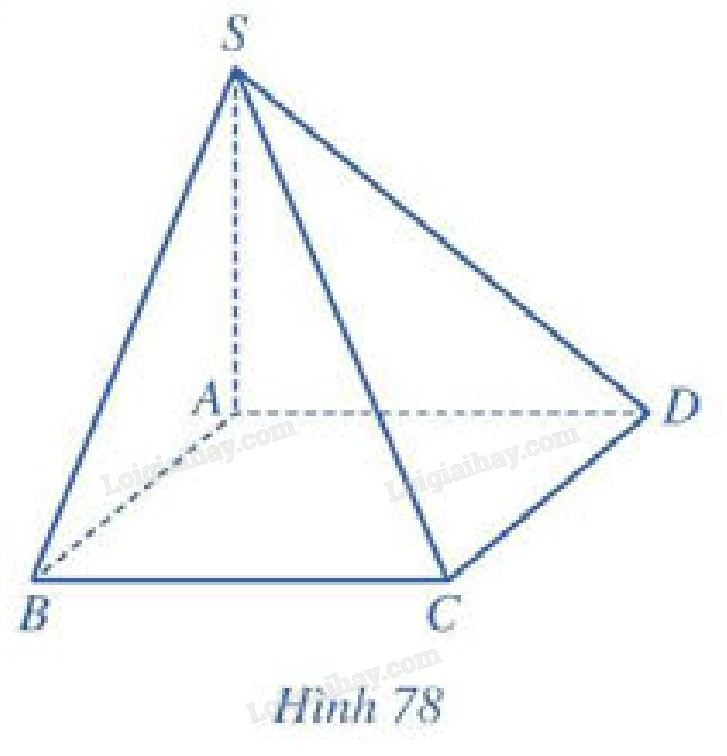
a) \(SA \bot \left( {ABCD} \right) \Rightarrow SA \bot C{\rm{D}}\)
\(ABCD\) là hình vuông \( \Rightarrow A{\rm{D}} \bot C{\rm{D}}\)
\(\begin{array}{l} \Rightarrow C{\rm{D}} \bot \left( {SA{\rm{D}}} \right) \Rightarrow C{\rm{D}} \bot S{\rm{D}}\\ \Rightarrow d\left( {S,C{\rm{D}}} \right) = S{\rm{D}} = \sqrt {S{A^2} + A{{\rm{D}}^2}} = a\sqrt 2 \end{array}\)
b) \(SA \bot \left( {ABCD} \right) \Rightarrow SA \bot A{\rm{D}}\)
\(ABCD\) là hình vuông \( \Rightarrow A{\rm{B}} \bot A{\rm{D}}\)
\( \Rightarrow A{\rm{D}} \bot \left( {SA{\rm{B}}} \right) \Rightarrow d\left( {D,\left( {SAB} \right)} \right) = A{\rm{D}} = a\)
c) Kẻ \(AH \bot S{\rm{D}}\left( {H \in S{\rm{D}}} \right)\).
\(C{\rm{D}} \bot \left( {SA{\rm{D}}} \right) \Rightarrow C{\rm{D}} \bot AH\)
\( \Rightarrow AH \bot \left( {SC{\rm{D}}} \right) \Rightarrow d\left( {A,\left( {SC{\rm{D}}} \right)} \right) = AH\)
Tam giác \(SAD\) vuông tại \(A\) có đường cao \(AH\)
\( \Rightarrow AH = \frac{{SA.A{\rm{D}}}}{{S{\rm{D}}}} = \frac{{a\sqrt 2 }}{2}\)
Vậy \(d\left( {A,\left( {SC{\rm{D}}} \right)} \right) = \frac{{a\sqrt 2 }}{2}\).
Đúng 1
Bình luận (0)
a) Tính khoảng cách từ điểm \(O\left( {0{\rm{;}}0} \right)\) đến đường thẳng \(\Delta \):\(\frac{x}{{ - 4}} + \frac{y}{2} = 1\)
b) Tính khoảng cách giữa hai đường thẳng song song \({\Delta _1}:x - y + 1 = 0\)và \({\Delta _2}:x - y - 1 = 0\)
a) Ta có: \(\Delta \):\(\frac{x}{{ - 4}} + \frac{y}{2} = 1 \Leftrightarrow x - 2y + 4 = 0\)
Vậy khoảng cách từ O đến \(\Delta \) là: \(d\left( {O;\Delta } \right) = \frac{{\left| {1.0 - 2.0 + 4} \right|}}{{\sqrt {{1^2} + {2^2}} }} = \frac{{4\sqrt 5 }}{5}\)
b) Lấy \(M\left( {0;1} \right) \in {\Delta _1}\)
Suy ra: \(d\left( {{\Delta _1},{\Delta _2}} \right) = d\left( {M,{\Delta _2}} \right) = \frac{{\left| {0 - 1 - 1} \right|}}{{\sqrt {{1^2} + {{\left( { - 1} \right)}^2}} }} = \sqrt 2 \)
Đúng 0
Bình luận (0)
: Kinh độ của 1 điểm là
A. khoảng cách tính bằng độ từ điểm đó đến xích đạo.
B. khoảng cách tính bằng độ từ điểm đó đến cực.
C. khoảng cách tính bằng độ từ điểm đó đến vĩ tuyến đi qua điểm đó.
khoảng cách tính bằng độ từ kinh tuyến gốc đến kinh tuyến đi qua điểm đó
Xem thêm câu trả lời
1.Một ô tô chạy từ A đến B với vận tốc 65km/h, cùng lúc đó 1 xe máy chạy từ B đến A với vận tốc 40km/h.Biết khoảng cách AB là 540km và M là trung điểm của AB.Hỏi sau khi khổi hành bao nhiêu thì ô tô cách M một khoảng bằng 1/2 khoảng cách từ xe máy đến M2.Tính:B 1 + frac{1}{2}left(1+2right)+frac{1}{3}left(1+2+3right)+frac{1}{4}left(1+2+3+4right)+...+frac{1}{20}left(1+2+3+...+20right)3.Độ dài 3 cạnh của tam giác tỉ lệ với 2;3;4.Hỏi 3 chiều cao tương ứng 3 cạnh đó tỉ lệ với số nào?
Đọc tiếp
1.Một ô tô chạy từ A đến B với vận tốc 65km/h, cùng lúc đó 1 xe máy chạy từ B đến A với vận tốc 40km/h.Biết khoảng cách AB là 540km và M là trung điểm của AB.Hỏi sau khi khổi hành bao nhiêu thì ô tô cách M một khoảng bằng 1/2 khoảng cách từ xe máy đến M
2.Tính:
B = 1 + \(\frac{1}{2}\left(1+2\right)+\frac{1}{3}\left(1+2+3\right)+\frac{1}{4}\left(1+2+3+4\right)+...+\frac{1}{20}\left(1+2+3+...+20\right)\)
3.Độ dài 3 cạnh của tam giác tỉ lệ với 2;3;4.Hỏi 3 chiều cao tương ứng 3 cạnh đó tỉ lệ với số nào?
Bài 1:
Nửa quãng đường AB( hay M cách A, B) dài là:
540:2=270(km)
Gọi quãng đường ô tô và xe máy đã đi lần lượt là S1; S2 (km) và t (giờ) là thời gian cần tìm.
Trong cùng 1 thời gian đi thì quãng đường tỉ lệ thuận với vận tốc.
\(\Rightarrow\frac{S_1}{65}=\frac{S_2}{40}=t\)
Ta có:
\(S_1=\frac{1}{2}\cdot S_2\)
\(\Rightarrow t=\frac{270-a}{65}=\frac{540-2a}{130}=\frac{270-2a}{40}\)
Áp dụng tính chất dãy tỉ số bằng nhau, ta có:
\(t=\frac{540-2a}{130}=\frac{270-2a}{40}=\frac{\left(540-2a\right)-\left(270-2a\right)}{130-40}=\frac{270}{90}=3\)
Vậy sau khi khởi hành 3 giờ thì ô tô cách M 1 khoảng bằng \(\frac{1}{2}\) khoảng cách từ xe máy đến M.
Đúng 0
Bình luận (2)
Hai điểm A và B thuộc cùng một nửa mặt phẳng có bờ là đường thẳng xy. Khoảng cách từ điểm A đến xy bằng 12cm, khoảng cách từ điểm B đến xy bằng 20cm. Tính khoảng cách từ trung điểm C của AB đến xy.
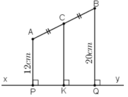
Gọi P, Q, K lần lượt là chân đường vuông góc hạ từ A, B, C xuống xy.
+ AP ⊥ xy và BQ ⊥ xy ⇒ AP // BQ
⇒ Tứ giác ABQP là hình thang.
+ CK ⊥ xy ⇒ CK // AP//BQ
+ Hình thang ABQP có AC = CB (gt) và CK // AP // BQ
⇒ PK = KQ
⇒ CK là đường trung bình của hình thang
⇒ CK = (AP + BQ)/2.
Mà AP = 12cm, BQ = 20cm ⇒ CK = 16cm.
Vậy khoảng cách từ trung điểm C của AB đến xy bằng 16cm.
Đúng 0
Bình luận (0)
tính khoảng cách điiểm gốc o đến mỗi điểm M,Q,R theo mẫu M -6 N -2 0 1 P Q R 7
mẫu khoảng cách từ 0 đến điểm N là 2 đơn vị
khoảng cách từ 0 đến P là 1 đơn vị
b) tính khoảng cách từ điểm gốc 0đến các điểm biểu diễn các số:-8;6;-50;15
a) Hãy biểu diễn hai số -5 và 5 trên cùng một trục số.
b) Tính khoảng cách từ điểm 5 đến điểm 0.
c) Tính khoảng cách từ điểm -5 đến điểm 0.
a)

b) Khoảng cách từ điểm 5 đến điểm 0 là: 5 đơn vị
c) Khoảng cách từ điểm - 5 đến điểm 0 là: 5 đơn vị
Đúng 0
Bình luận (0)
Cho h/chóp S.ABC có đáy ABC là tam giác đều cạnh bằng a, \(SA\perp\left(ABC\right)\), SA = 2a. Gọi P là điểm trên cạnh AB sao cho \(BP=\dfrac{1}{3}AB\). Tính khoảng cách từ điểm B đến mặt phẳng (SPC).
\(BP=\dfrac{1}{3}AB\Rightarrow BP=\dfrac{1}{2}AP\)
\(\Rightarrow d\left(B;\left(SPC\right)\right)=\dfrac{1}{2}d\left(A;\left(SPC\right)\right)\)
Trong tam giác APC, kẻ \(AH\perp CP\Rightarrow CP\left(SAH\right)\)
Trong tam giác vuông SAH, kẻ \(AK\perp SH\Rightarrow AK\perp\left(SPC\right)\Rightarrow AK=d\left(A;\left(SPC\right)\right)\)
\(AP=\dfrac{2}{3}AB=\dfrac{2a}{3}\Rightarrow CP=\sqrt{AP^2+AC^2-2AP.AC.cos60^0}=\dfrac{a\sqrt{7}}{3}\)
Áp dụng định lý hàm sin:
\(\dfrac{AP}{sin\widehat{ACP}}=\dfrac{CP}{sinA}\Rightarrow sin\widehat{ACP}=\dfrac{AP.sin60^0}{CP}=\dfrac{\sqrt{21}}{7}\)
\(\Rightarrow AH=AC.sin\widehat{ACP}=\dfrac{a\sqrt{21}}{7}\)
\(\dfrac{1}{AK^2}=\dfrac{1}{AH^2}+\dfrac{1}{SA^2}\Rightarrow AK=\dfrac{SA.AH}{\sqrt{SA^2+AH^2}}=\dfrac{2a\sqrt{93}}{31}\)
\(\Rightarrow d\left(B;\left(SPC\right)\right)=\dfrac{1}{2}AK=\dfrac{a\sqrt{93}}{31}\)
Bạn kiểm tra lại phần tính toán
Đúng 2
Bình luận (0)





