Đáp án A.

Ta có A M ⊥ B C ⊥ O A ⇒ B C ⊥ O A M ⇒ B C ⊥ O M  

Tương tự ta cũng có O M ⊥ A C ⇒ O M ⊥ P ⇒ P  (P) nhận O M ¯ = 3 ; 2 ; 1  là vecto pháp tuyến.

Trong các đáp án, chọn đáp án mặt phẳng có vecto pháp tuyến có cùng giá với O M ¯  và không chứa điểm M thì thỏa.

Chọn A

Gọi A(a;0;0);B(0;b;0);C(0;0;c)

Phương trình mặt phẳng (P) có dạng:

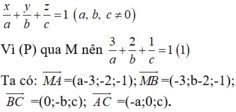
Vì M là trực tâm của tam giác ABC nên:

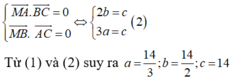
Khi đó phương trình (P): 3x+2y+z-14=0.

Vậy mặt phẳng song song với (P) là: 3x+2y+z+14=0.

vecto AH=(x+2;y-4); vecto BC=(-6;-2)

vecto BH=(x-4;y-1); vecto AC=(0;-5)

Theo đề, ta có: -6(x+2)-2(y-4)=0 và 0(x-4)-5(y-1)=0

=>y=1 và -6(x+2)=2(y-4)=2*(1-4)=-6

=>x+2=1 và y=1

=>x=-1 và y=1

Theo tính chất đường phân giác của tam giác ta có  E A E B = O A O B = 2 2 .

Vì E nằm giữa hai điểm A, B nên E A → = − 2 2 E B → . *  

Gọi E(x; y). Ta có  E A → = 1 − x ; 3 − y E B → = 4 − x ; 2 − y .

Từ (*), suy ra  1 − x = − 2 2 4 − x 3 − y = − 2 2 2 − y ⇔ x = − 2 + 3 2 y = 4 − 2 .

 Chọn D.

gọi Pt đường thảng .....y=ax+b(d)

d đi qua M(-1,1)   1=-a+b⇔b=a+1

gọi d cắt Ox tại \(A\left(-\dfrac{b}{a},O\right)\)

d cắt Oy tại \(B\left(O,b\right)\)

\(\Delta AOB\) vuông cân tại o

\(\Rightarrow OA=OB\Rightarrow\left(-\dfrac{b}{a}\right)^2+o^2=o^2+b^2\)

\(\dfrac{b^2}{a^2}=b^2\Leftrightarrow\dfrac{1}{a^2}=1\Leftrightarrow a^2=1\)

\(\Leftrightarrow\left[{}\begin{matrix}a=1\\a=-1\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}b=2\\b=0\left(loại\right)\end{matrix}\right.\)

(do d cắt 2 trục tọa độ nên a,b≠0)

vậy PtT đg thảng d:y=x+2

Gọi pt đường thẳng có dạng \(y=ax+b\)

Đường thẳng qua M tạo 2 trục tọa độ 1 tam giác vuông cân khi nó có hệ số góc \(a=1\) hoặc \(a=-1\)

\(\Rightarrow\left[{}\begin{matrix}y=x+b\\y=-x+b\end{matrix}\right.\)

Thay tọa độ M vào phương trình ta được:

\(\left[{}\begin{matrix}1=-1+b\\1=-\left(-1\right)+b\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}b=2\\b=0\end{matrix}\right.\)

Có 2 đường thẳng thỏa mãn: \(\left[{}\begin{matrix}y=x+2\\y=-x\end{matrix}\right.\)

1, Gọi tọa độ điểm D(x;y)

Ta có:\(\overrightarrow{AB}\left(8;1\right)\)

\(\overrightarrow{DC}\left(1-x;5-y\right)\)

Tứ giác ABCD là hình bình hành khi

\(\overrightarrow{AB}=\overrightarrow{DC}\)

\(\Leftrightarrow1-x=8;5-y=1\)

\(\Leftrightarrow\left\{{}\begin{matrix}x=-7\\y=4\end{matrix}\right.\)

Vậy tọa độ điểm D(-7;4)

Đáp án : D

ai giúp mình câu b với 

a: \(AB=\sqrt{\left[2-\left(-2\right)\right]^2+\left(-1-2\right)^2}=5\)

\(BC=\sqrt{\left(5-2\right)^2+\left(3+1\right)^2}=5\)

Do đó: AB=BC

hay ΔABC cân tại B