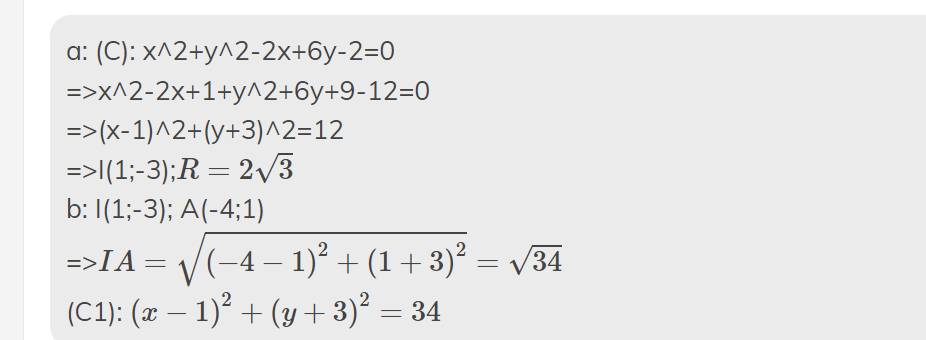Viết phương trình đường tròn (C) có tâm I(-2;1), ctắ đường thẳng Δ: x-2y+3=0 tại hai điểm A, B thỏa mãn: AB=2
MA
Những câu hỏi liên quan
1. viết phương trình đường tròn ngoại tiếp tam giác ABC biết A(-1,1);B(1,3);C(1,-1)
2. viết phương trình đường tròn có tâm I(-2,3) và đi qua M(2,-3)
3. viết phương trình đường tròn có tâm I nằm trên đường thẳng 4x-2y-8=0 biết đường tròn đó tiếp xúc với trục tọa độ
Câu 20: Trong mặt phăng tọa độ Oxy, cho điểm I(4;3), đường thăng d:3x+4y-4=0 và đường tròn (C):x²+y²-2x+6y-2=0.
a) Tìm tọa độ tâm và bán kính R của đường tròn (C).
b) Viết phương trình đường tròn có tâm I và đi qua A(-4;1)
c) Viết phương trình đườNg tròn (C') có tâm là I và cắt d tại hai điếm M, N sao cho MN =6
a) Để tìm tọa độ tâm và bán kính của đường tròn ©, ta cần viết lại phương trình của nó dưới dạng chuẩn:
\begin{align*}
x^2 + y^2 - 2x + 6y - 2 &= 0 \
\Leftrightarrow (x-1)^2 + (y+3)^2 &= 14
\end{align*}
Vậy, tọa độ tâm của đường tròn © là $(1,-3)$ và bán kính của đường tròn © là $\sqrt{14}$.
b) Đường tròn có tâm $I(4,3)$ và đi qua $A(-4,1)$ có phương trình là:
$$(x-4)^2 + (y-3)^2 = (-4-4)^2 + (1-3)^2 = 20$$
c) Để tìm phương trình đường tròn (C') có tâm là $I(4,3)$ và cắt đường thẳng $d: 3x+4y-4=0$ tại hai điểm $M$ và $N$ sao cho $MN=6$, ta có thể làm như sau:
Tìm giao điểm $H$ của đường thẳng $d$ và đường vuông góc với $d$ đi qua $I$.Tìm hai điểm $M$ và $N$ trên đường thẳng $d$ sao cho $HM=HN=3$.Xây dựng đường tròn (C') có tâm là $I$ và bán kính bằng $IN=IM=\sqrt{3^2+4^2}=5$.
Để tìm giao điểm $H$, ta cần tìm phương trình của đường thẳng vuông góc với $d$ đi qua $I$. Đường thẳng đó có phương trình là:
$$4x - 3y - 7 = 0$$
Giao điểm $H$ của đường thẳng này và $d$ có tọa độ là $(\frac{52}{25}, \frac{9}{25})$.
Để tìm hai điểm $M$ và $N$, ta có thể sử dụng công thức khoảng cách giữa điểm và đường thẳng. Khoảng cách từ điểm $H$ đến đường thẳng $d$ là:
$$d(H,d) = \frac{|3\cdot \frac{52}{25} + 4\cdot \frac{9}{25} - 4|}{\sqrt{3^2+4^2}} = \frac{1}{5}$$
Vậy, hai điểm $M$ và $N$ cách $H$ một khoảng bằng $\frac{3}{5}$ và $\frac{4}{5}$ đơn vị theo hướng vuông góc với $d$. Ta có thể tính được tọa độ của $M$ và $N$ như sau:
$$M = \left(\frac{52}{25} - \frac{4}{5}\cdot 4, \frac{9}{25} + \frac{3}{5}\cdot 3\right) = \left(\frac{12}{25}, \frac{54}{25}\right)$$
và
$$N = \left(\frac{52}{25} + \frac{4}{5}\cdot 4, \frac{9}{25} + \frac{4}{5}\cdot 3\right) = \left(\frac{92}{25}, \frac{27}{5}\right)$$
Cuối cùng, phương trình đường tròn (C') có tâm là $I(4,3)$ và cắt đường thẳng $d$ tại hai điểm $M$ và $N$ sao cho $MN=6$ là:
$$(x-4)^2 + (y-3)^2 = 5^2$$
Đúng 0
Bình luận (0)
Câu 20: Trong mặt phăng tọa độ Oxy, cho điểm I(4;3), đường thăng d:3x+4y-4=0 và đường tròn (C):x²+y²-2x+6y-2=0.
a) Tìm tọa độ tâm và bán kính R của đường tròn (C).
b) Viết phương trình đường tròn có tâm I và đi qua A(-4;1)
c) Viết phương trình đườNg tròn (C') có tâm là I và cắt d tại hai điếm M, N sao cho MN =6
Giải thích cụ thể câu c cho mình.
a: (C): x^2+y^2-2x+6y-2=0
=>x^2-2x+1+y^2+6y+9-12=0
=>(x-1)^2+(y+3)^2=12
=>I(1;-3);\(R=2\sqrt{3}\)
b: I(1;-3); A(-4;1)
=>\(IA=\sqrt{\left(-4-1\right)^2+\left(1+3\right)^2}=\sqrt{34}\)
(C1): \(\left(x-1\right)^2+\left(y+3\right)^2=34\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Câu 20: Trong mặt phăng tọa độ Oxy, cho điểm I(4;3), đường thăng d:3x+4y-4=0 và đường tròn (C):x²+y²-2x+6y-2=0.
a) Tìm tọa độ tâm và bán kính R của đường tròn (C).
b) Viết phương trình đường tròn có tâm I và đi qua A(-4;1)
c) Viết phương trình đườNg tròn (C') có tâm là I và cắt d tại hai điếm M, N sao cho MN =6
Giải thích cụ thể câu c cho mình.
Viết phương trình đường tròn (C) có tâm I(2;-2) và tiếp xúc với đường thẳng x + y + 2 = 0?
Vì (C) tiếp xúc với đường thẳng d: x + y + 2 = 0 nên (C) có bán kính
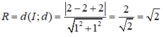
Vậy đường tròn (C) có dạng: (x - 2 ) 2 + (y + 2 ) 2 = 2
Đúng 0
Bình luận (0)
a) viết phương trình đường tròn (C) có tâm I(2,3) đi qua điểm A(5,7) b) viết phương trình tiếp tuyến của đường tròn (C) : (x-1)^2 + ( y+5)^2 =4 . Biết tiếp tuyến song song với đường thẳng (d) 3x + 4y - 1 =0
a) Để tìm phương trình đường tròn © có tâm I(2,3) đi qua điểm A(5,7), ta sử dụng công thức khoảng cách từ điểm đến tâm đường tròn:
$I\hat{A} = \sqrt{(x_A - x_I)^2 + (y_A - y_I)^2}$
Với I là tâm đường tròn, A là điểm trên đường tròn.
Ta có: $x_I = 2$, $y_I = 3$, $x_A = 5$, $y_A = 7$
Thay vào công thức ta được:
$\sqrt{(5-2)^2 + (7-3)^2} = \sqrt{34}$
Vậy bán kính của đường tròn là $\sqrt{34}$.
Phương trình đường tròn © có tâm I(2,3) và bán kính $\sqrt{34}$ là:
$(x-2)^2 + (y-3)^2 = 34$
b) Để tìm phương trình tiếp tuyến của đường tròn © : $(x-1)^2 + ( y+5)^2 =4$, ta cần tìm đạo hàm của phương trình đường tròn tại điểm cần tìm tiếp tuyến.
Ta có phương trình đường tròn chính giữa:
$(x-1)^2 + (y+5)^2 = 2^2$
Đạo hàm hai vế theo x:
$2(x-1) + 2(y+5)y' = 0$
Suy ra:
$y' = -\frac{x-1}{y+5}$
Tại điểm M(x,y) trên đường tròn, ta có:
$(x-1)^2 + (y+5)^2 = 2^2$
Đạo hàm hai vế theo x:
$2(x-1) + 2(y+5)y' = 0$
Suy ra:
$y' = -\frac{x-1}{y+5}$
Vậy tại điểm M(x,y), phương trình tiếp tuyến của đường tròn là:
$y - y_M = y'(x-x_M)$
Thay $y'$ bằng $\frac{-(x-1)}{y+5}$ và $x_M$, $y_M$ bằng 1, -5 ta được:
$y + 5 = \frac{-(x-1)}{y+5}(x-1)$
Simplifying:
$x(y+5) + y(x-1) = 6$
Đường thẳng (d) có phương trình là $3x + 4y - 1 = 0$. Vì tiếp tuyến song song với đường thẳng (d) nên hệ số góc của tiếp tuyến
Đúng 2
Bình luận (1)
Trong mặt phẳng tọa độ Oxy, cho đường tròn tâm I(3;-2), bán kính 3.a. Viết phương trình của đường tròn đó.b. Viết phương trình ảnh của đường tròn (I;3) qua phép tịnh tiến theo vectơ v(-2 ;1).c. Viết phương trình ảnh của đường tròn (I;3) qua phép đối xứng trục Ox.d. Viết phương trình ảnh của đường tròn (I;3) qua phép đối xứng qua gốc tọa độ
Đọc tiếp
Trong mặt phẳng tọa độ Oxy, cho đường tròn tâm I(3;-2), bán kính 3.
a. Viết phương trình của đường tròn đó.
b. Viết phương trình ảnh của đường tròn (I;3) qua phép tịnh tiến theo vectơ v=(-2 ;1).
c. Viết phương trình ảnh của đường tròn (I;3) qua phép đối xứng trục Ox.
d. Viết phương trình ảnh của đường tròn (I;3) qua phép đối xứng qua gốc tọa độ
a. Phương trình đường tròn : (x – 3)2 + (y + 2)2 = 9.
b. (I1; R1) là ảnh của (I; 3) qua phép tịnh tiến theo vec tơ v.
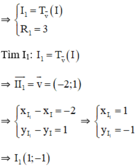
⇒ Phương trình đường tròn cần tìm: (x – 1)2 + ( y + 1)2 = 9.
c. (I2; R2) là ảnh của (I; 3) qua phép đối xứng trục Ox
⇒ R2 = 3 và I2 = ĐOx(I)
Tìm I2: I2 = ĐOx(I) ⇒ 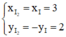 ⇒ I2(3; 2)
⇒ I2(3; 2)
⇒ Phương trình đường tròn cần tìm: (x – 3)2 + (y – 2)2 = 9.
d. (I3; R3) là ảnh của (I; 3) qua phép đối xứng qua gốc O.
⇒ R3 = 3 và I3 = ĐO(I)
Tìm I3: I3 = ĐO(I) ⇒ 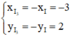
⇒ Phương trình đường tròn cần tìm: (x + 3)2 +(y – 2)2 = 9.
Đúng 0
Bình luận (0)
cho tam giác abc có a (1,3) b(-2,4) c (5,-1) a) viết phương trình đường tròn tâm B đi qua c b) viết phương trình đường tròn đường kính ac c) viết phương trình đường tròn tâm tiếp xúc cạnh bc d) viết phương trình ngoại tiếp tám giác anc
Trong mặt phẳng tọa độ Oxy cho đường tròn (C) có phương trình:
x
−
3
2
+
y
+
1
2
9
.Hãy viết phương trình của đường tròn (C’)...
Đọc tiếp
Trong mặt phẳng tọa độ Oxy cho đường tròn (C) có phương trình: x − 3 2 + y + 1 2 = 9 .
Hãy viết phương trình của đường tròn (C’) là ảnh của (C) qua phép vị tự tâm I(1; 2) tỉ số k = -2
Ta có A(3;−1) là tâm của (C) nên tâm A' của (C') là ảnh của A qua phép vị tự đã cho. Từ đó suy ra A′ = (−3;8). Vì bán kính của (C) bằng 3, nên bán kính của (C') bằng |−2|.3 = 6
Vậy (C') có phương trình: x + 3 2 + y − 8 2 = 36 .
Đúng 0
Bình luận (0)
viết phương trình đường tròn c đi qua a(1;0),b(0,1);và c có tâm i thuộc đường thẵng+y-2=0