giải phương trình;
x2 + x - \(\dfrac{7}{x^{2^{ }}+x+1}\) = 5
giải phương trình |x+1|+|x-1|=1+|x^2-1|giải phương trình |x+1|+|x-1|=1+|x^2-1|giải phương trình |x+1|+|x-1|=1+|x^2-1|giải phương trình |x+1|+|x-1|=1+|x^2-1|giải phương trình |x+1|+|x-1|=1+|x^2-1|
ta có :
\(\left|x+1\right|+\left|x-1\right|=1+\left|\left(x-1\right)\left(x+1\right)\right|\)
\(\Leftrightarrow\left|x-1\right|\left|x+1\right|-\left|x-1\right|-\left|x+1\right|+1=0\)
\(\Leftrightarrow\left(\left|x-1\right|-1\right)\left(\left|x+1\right|-1\right)=0\Leftrightarrow\orbr{\begin{cases}\left|x-1\right|=1\\\left|x+1\right|=1\end{cases}}\)
\(\Leftrightarrow x\in\left\{-2,0,2\right\}\)
Bài 1: Giải các bất phương trình và phương trình sau :
a) 2(3-4x) = 10-(2x – 5)
Giải các bất phương trình và phương trình sau :
a) 3(2-4x) = 11-(3x – 1)
Bài 1:
a) Ta có: \(2\left(3-4x\right)=10-\left(2x-5\right)\)
\(\Leftrightarrow6-8x-10+2x-5=0\)
\(\Leftrightarrow-6x+11=0\)
\(\Leftrightarrow-6x=-11\)
hay \(x=\dfrac{11}{6}\)
b) Ta có: \(3\left(2-4x\right)=11-\left(3x-1\right)\)
\(\Leftrightarrow6-12x-11+3x-1=0\)
\(\Leftrightarrow-9x-6=0\)
\(\Leftrightarrow-9x=6\)
hay \(x=-\dfrac{2}{3}\)
Nghiệm chung của ba phương trình đã cho được gọi là nghiệm của hệ gồm ba phương trình ấy. Giải hệ phương trình là tìm nghiệm chung của tất cả các phương trình trong hệ. Hãy giải các hệ phương trình sau: 3 x + 5 y = 34 4 x - 5 y = - 13 5 x - 2 y = 5

Thay x = 3, y = 5 vào vế trái của phương trình (3) ta được:
VT = 5.3 – 2.5 = 15 – 10 = 5 = VP
Vậy (x; y) = (3; 5) là nghiệm của phương trình (3).
Hệ phương trình đã cho có nghiệm (x; ) = (3; 5)
cho phương trình sau: x² - 2(m+1) -m - 1=0 a, Giải phương trình trên khi m=2 b, không giải phương trình tính giá trị biểu thức c,tìm giá trị nhỏ nhất của phương trình tại m=4
a: Khi m=2 thì pt sẽ là x^2-6x-3=0
=>\(x=3\pm2\sqrt{3}\)
Nghiệm chung của ba phương trình đã cho được gọi là nghiệm của hệ gồm ba phương trình ấy. Giải hệ phương trình là tìm nghiệm chung của tất cả các phương trình trong hệ. Hãy giải các hệ phương trình sau: 6 x - 5 y = - 49 - 3 x + 2 y = 22 7 x + 5 y = 10

Thay x = -3, y = 31/5 vào vế trái của phương trình (2), ta được:
VT = -3.(-3) + 2.31/5 = 9 + 62/5 = 107/5 ≠ 22 = VP
Vậy (x; y) = (-3; 31/5 ) không phải là nghiệm của phương trình (2).
Hệ phương trình đã cho vô nghiệm.
Nêu cách giải phương trình lượng giác cơ bản , cách giải phương trình a sin x + b cos x = c .
a) Cách giải các phương trình lượng giác cơ bản:
+ Phương trình sin x = a.
Nếu |a| > 1 ⇒ phương trình vô nghiệm.
Nếu |a| ≤ 1 ⇒ tìm một cung α sao cho sin α = a.
Khi đó phương trình trở thành sin x = sin α
⇒ Phương trình có nghiệm: 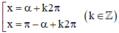
+ Phương trình cos x = a.
Nếu |a| > 1 ⇒ phương trình vô nghiệm.
Nếu |a| ≤ 1 ⇒ tìm một cung α sao cho cos α = a.
Khi đó phương trình trở thành cos x = cos α.
⇒ Phương trình có nghiệm: x = ±α + k2π (k ∈ Z).
+ Phương trình tan x = a.
Tìm một cung α sao cho tan α = a.
Khi đó phương trình trở thành tan x = tan α.
⇒ Phương trình có nghiệm x = α + kπ (k ∈ Z).
+ Phương trình cot x = a
Tìm một cung α sao cho cot α = a.
Khi đó phương trình trở thành cot x = cot α.
⇒ Phương trình có nghiệm x = α + kπ (k ∈ Z).
b) Cách giải phương trình a.sin x + b.cos x = c.
+ Nếu a = 0 hoặc b = 0 ⇒ Phương trình lượng giác cơ bản .
+ a ≠ 0 và b ≠ 0. Chia cả hai vế của phương trình cho  ta được:
ta được:

Ta giải phương trình trên như phương trình lượng giác cơ bản.
Giải phương trình và hệ phương trình 
\(x^2-\left(2-\sqrt{3}\right)x-2\sqrt{3}=0\)
\(\Delta=\left[-\left(2-\sqrt{3}\right)^2\right]-4\left(-2\sqrt{3}\right)\)
\(=\left(4-4\sqrt{3}+3\right)+8\sqrt{3}=7+4\sqrt{3}=\sqrt{3}^2+2.2.\sqrt{3}+2^2=\left(\sqrt{3}+2\right)^2>0\)
=> pt có 2 nghiệm phân biệt
\(\left\{{}\begin{matrix}x_1=\dfrac{2-\sqrt{3}-\sqrt{3}-2}{2}=\dfrac{-2\sqrt{3}}{2}=-\sqrt{3}\\x_2=\dfrac{2-\sqrt{3}+\sqrt{3}+2}{2}=\dfrac{4}{2}=2\end{matrix}\right.\)
Tìm sai lầm trong các "lời giải" sau:
a) Giải bất phương trình -2x > 23. Ta có:
-2x > 23 ⇔ x > 23 + 2 ⇔ x > 25.
Vậy nghiệm của bất phương trình là x > 25.
b) Giải bất phương trình 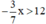 . Ta có:
. Ta có:
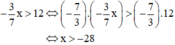
a) Sai lầm là coi -2 là hạng từ và chuyển vế hạng tử này trong khi -2 là một nhân tử.
Lời giải đúng:
-2x > 23
⇔ x < 23 : (-2) (chia cho số âm nên đổi chiều)
⇔ x < -11,5
Vậy nghiệm của bất phương trình là x < -11,5
b) Sai lầm là nhân hai vế của bất phương trình với 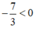 mà không đổi chiều bất phương trình.
mà không đổi chiều bất phương trình.
Lời giải đúng:
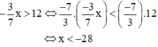
Vậy nghiệm của bất phương trình là x < -28
Cho phương trình (ẩn x):x+a/a-x - x-a/a+x=a(3a+1)/a^2-x^2
Giải phương trình với a=-3Giải phương trình với a=1Giải phương trình với a=0Tìm các giá trị của a sao cho phương trình nhận x=1/2 làm nghiệm
1. a = 3 thì phương trình trở thành:
\(\frac{x+3}{3-x}-\frac{x-3}{3+x}=\frac{-3\left[3.\left(-3\right)+1\right]}{\left(-3\right)^2}-x^2\)
\(\Leftrightarrow\frac{\left(x+3\right)^2+\left(3-x\right)^2}{\left(3-x\right)\left(3+x\right)}=\frac{-3\left[-9+1\right]}{9}-x^2\)
\(\Leftrightarrow\frac{x^2+6x+9+x^2-6x+9}{\left(3-x\right)\left(3+x\right)}=\frac{-3.\left(-8\right)}{9}-x^2\)
\(\Leftrightarrow\frac{2x^2+18}{9-x^2}=\frac{24}{9}-x^2\)
\(\Leftrightarrow\frac{2x^2+18}{9-x^2}+x^2=\frac{24}{9}\)
\(\Leftrightarrow\frac{2x^2+18+9x^2-x^4}{9-x^2}=\frac{24}{9}\)
\(\Leftrightarrow\frac{11x^2+18-x^4}{9-x^2}=\frac{24}{9}\)
\(\Leftrightarrow99x^2+18-9x^4=216-24x^2\)
\(\Leftrightarrow9x^4-123x^2+198=0\)
Đặt \(x^2=t\left(t\ge0\right)\)
Phương trình trở thành \(9t^2-123t+198=0\)
Ta có \(\Delta=123^2-4.9.198=8001,\sqrt{\Delta}=3\sqrt{889}\)
\(\Rightarrow\orbr{\begin{cases}t=\frac{123+3\sqrt{889}}{18}=\frac{41+\sqrt{889}}{6}\\t=\frac{123-3\sqrt{889}}{18}=\frac{41-\sqrt{889}}{6}\end{cases}}\)
Lúc đó \(\orbr{\begin{cases}x^2=\frac{41+\sqrt{889}}{6}\\x^2=\frac{41-\sqrt{889}}{6}\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=\pm\sqrt{\frac{41+\sqrt{889}}{6}}\\x=\pm\sqrt{\frac{41-\sqrt{889}}{6}}\end{cases}}\)
Vậy pt có 4 nghiệm \(S=\left\{\pm\sqrt{\frac{41+\sqrt{889}}{6}};\pm\sqrt{\frac{41-\sqrt{889}}{6}}\right\}\)
Sửa)):
a = -3 mà ghi lôn a = 3.giải tương tự như 3
Giải giúp mình với Cho phương trình x bình phương - mx + m -1=0 a) Giải phương trình khi m=5 b)Tìm m để phương trình có nghiệm phân biệt x1,x2 sao cho x2=2x1.
a: x^2-mx+m-1=0
Khi m=5 thì (1) sẽ là x^2-5x+4=0
=>x=1 hoặc x=4
b:Δ=(-m)^2-4(m-1)=m^2-4m+4=(m-2)^2
Để phươg trình có 2 nghiệm phân biệt thì m-2<>0
=>m<>2
x2=2x1
x2+x1=m
=>3x1=m và x2=2x1
=>x1=m/3 và x2=2/3m
x1*x2=m-1
=>2/9m^2-m+1=0
=>2m^2-9m+9=0
=>2m^2-3m-6m+9=0
=>(2m-3)(m-3)=0
=>m=3 hoặc m=3/2