x , y > 0 ; x + 2y\(\ge\)2
Tìm min A = 2x2 + 16y2 + \(\frac{2}{x}+\frac{3}{y}\)
|x-3| + |y-2x | =0
|x| + 3|2x -x ² | =0
|5x ² -5 | + 4|y-7 | =0
||x +1 | + |y-5 |=0
|x ² -1| + |y-1| =0
|x-1 | +|x ²-x |=0
a) Ta có: \(\left|x-3\right|+\left|y-2x\right|=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}x-3=0\\y-2x=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=3\\y=2x=2\cdot3=6\end{matrix}\right.\)
bạn tin lúc trước tớ nói không tớ sai ở chổ 1x0 đóooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooo
|x-3| + |y-2x | =0 |x| + 3|2x -x ² | =0 |5x ² -5 | + 4|y-7 | =0 ||x +1 | + |y-5 |=0 |x ² -1| + |y-1| =0 |x-1 | +|x ²-x |=0
a) Ta có: \(\left|x-3\right|+\left|y-2x\right|=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}x-3=0\\y-2x=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=3\\y=2x=2\cdot3=6\end{matrix}\right.\)
Cho x ≠ 0,y ≠ 0,z ≠ 0 và x+y+z=0.CMR:\(\left(\dfrac{x-y}{z}+\dfrac{y-z}{x}+\dfrac{x-z}{y}\right)\left(\dfrac{z}{x-y}+\dfrac{x}{y-z}+\dfrac{y}{x-z}\right)=9\)
Đặt \(\dfrac{x-y}{z}=m,\dfrac{y-z}{x}=n,\dfrac{z-x}{y}=p\), ta có:
\(\left(m+n+p\right)\left(\dfrac{1}{m}+\dfrac{1}{n}+\dfrac{1}{p}\right)=3+\dfrac{n+p}{m}+\dfrac{p+m}{n}+\dfrac{m+n}{p}\)
Tính \(\dfrac{n+p}{m}\) theo x, y, z ta được:
\(\dfrac{n+p}{m}=\dfrac{z}{x-y}.\dfrac{y^2-yz+xz-x^2}{xy}=\dfrac{z}{xy}\left(-x-y+x\right)\)
\(=\dfrac{z}{xy}\left(-x-y-z+2z\right)=\dfrac{2x^2}{xy}\) vì \(\left(x+y+z\right)=0\)
Tương tự: \(\dfrac{m+p}{n}=\dfrac{2x^2}{yz}.\dfrac{m+n}{p}=\dfrac{2y^2}{xz}\)
Vậy \(\left(m+n+p\right)\left(\dfrac{1}{m}+\dfrac{1}{n}+\dfrac{1}{p}\right)=3+\dfrac{2\left(x^3+y^3+z^3\right)}{xyz}=3+\dfrac{2.3xyz}{xyz}=3+6=9\)
Rút gọn các biểu thức sau:
a) A=\(\dfrac{x\sqrt{y}+y\sqrt{x}}{x+2\sqrt{xy}+y}\)(x≥0 , y≥0 , xy≠0)
b) B=\(\dfrac{x\sqrt{y}-y\sqrt{x}}{x-2\sqrt{xy}+y}\)(x≥0 , y≥0 , x≠y)
c) C=\(\dfrac{3\sqrt{a}-2a-1}{4a-4\sqrt{a}+1}\)(a≥0 , a≠\(\dfrac{1}{4}\))
d) D=\(\dfrac{a+4\sqrt{a}+4}{\sqrt{a}+2}+\dfrac{4-a}{\sqrt{a}-2}\)(a≥0 , a≠4)
a) \(A=\dfrac{x\sqrt{y}+y\sqrt{x}}{x+2\sqrt{xy}+y}\)
\(A=\dfrac{\sqrt{xy}\left(\sqrt{x}+\sqrt{y}\right)}{\left(\sqrt{x}+\sqrt{y}\right)^2}\)
\(A=\dfrac{\sqrt{xy}}{\sqrt{x}+\sqrt{y}}\)
b) \(B=\dfrac{x\sqrt{y}-y\sqrt{x}}{x-2\sqrt{xy}+y}\)
\(B=\dfrac{\sqrt{xy}\left(\sqrt{x}-\sqrt{y}\right)}{\left(\sqrt{x}-\sqrt{y}\right)^2}\)
\(B=\dfrac{\sqrt{xy}}{\sqrt{x}-\sqrt{y}}\)
c) \(C=\dfrac{3\sqrt{a}-2a-1}{4a-4\sqrt{a}+1}\)
\(C=\dfrac{-\left(2a-3\sqrt{a}+1\right)}{\left(2\sqrt{a}\right)^2-2\sqrt{a}\cdot2\cdot1+1^2}\)
\(C=\dfrac{-\left(\sqrt{a}-1\right)\left(2\sqrt{a}-1\right)}{\left(2\sqrt{a}-1\right)^2}\)
\(C=\dfrac{-\sqrt{a}+1}{2\sqrt{a}-1}\)
d) \(D=\dfrac{a+4\sqrt{a}+4}{\sqrt{a}+2}+\dfrac{4-a}{\sqrt{a}-2}\)
\(D=\dfrac{\left(\sqrt{a}+2\right)^2}{\sqrt{a}+2}+\dfrac{\left(2-\sqrt{a}\right)\left(2+\sqrt{a}\right)}{\sqrt{a}-2}\)
\(D=\sqrt{a}+2-\dfrac{\left(\sqrt{a}-2\right)\left(\sqrt{a}+2\right)}{\sqrt{a}-2}\)
\(D=\left(\sqrt{a}+2\right)-\left(\sqrt{a}+2\right)\)
\(D=0\)
Trong các cặp hình phẳng giới hạn bởi các đường sau, cặp nào có diện tích bằng nhau?
a) {y = x + sinx, y = x với 0 ≤ x ≤ π} và {y = x + sinx, y = x với π ≤ x ≤ 2π}
b) {y = sinx, y = 0 với 0 ≤ x ≤ π} và {y = cosx, y = 0 với 0 ≤ x ≤ π};
c) {y = √x, y = x 2 }
và { 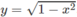 , y = 1 − x}
, y = 1 − x}
Cho x≠0;y≠0;z≠0 và x+y+z=0. Chứng minh rằng
\(\left(\dfrac{x-y}{z}+\dfrac{y-z}{x}+\dfrac{x-z}{y}\right)\left(\dfrac{z}{x-y}+\dfrac{x}{y-z}+\dfrac{y}{x-z}\right)=9\)
Đặt \(P=\left(\dfrac{x-y}{z}+\dfrac{y-z}{x}+\dfrac{z-x}{y}\right)\left(\dfrac{z}{x-y}+\dfrac{x}{y-z}+\dfrac{y}{z-x}\right)=9\)
Đặt \(\left\{{}\begin{matrix}\dfrac{x-y}{z}=a\\\dfrac{y-z}{x}=b\\\dfrac{x-z}{y}=c\end{matrix}\right.\)
\(\Leftrightarrow P=\left(a+b+c\right)\left(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\right)\\ =1+\dfrac{a}{b}+\dfrac{a}{c}+\dfrac{b}{a}+1+\dfrac{b}{c}+\dfrac{c}{a}+\dfrac{c}{b}+1\\ =3+\dfrac{a+c}{b}+\dfrac{a+b}{c}+\dfrac{b+c}{a}\)
Ta có \(\dfrac{a+c}{b}=\dfrac{\dfrac{x-y}{z}+\dfrac{z-x}{y}}{\dfrac{y-z}{x}}=\dfrac{xy-y^2+z^2-xz}{yz}\cdot\dfrac{x}{y-z}\)
\(=\dfrac{\left(z-y\right)\left(y+z-x\right)x}{yz\left(y-z\right)}=\dfrac{x\left(x-y-z\right)}{yz}\)
Mà \(x+y+z=0\Leftrightarrow x=-y-z\)
\(\Leftrightarrow\dfrac{a+c}{b}=\dfrac{x\left(x+x\right)}{yz}=\dfrac{2x^2}{yz}\)
Cmtt ta được \(\dfrac{a+b}{c}=\dfrac{2y^2}{xz};\dfrac{b+c}{a}=\dfrac{2z^2}{xy}\)
Cộng vế theo vế
\(\Leftrightarrow P=\dfrac{2x^2}{yz}+\dfrac{2y^2}{xz}+\dfrac{2z^2}{xy}+3=\dfrac{2x^3+2y^3+2z^3}{xyz}+3\\ \Leftrightarrow P=\dfrac{2\left(x^3+y^3+z^3\right)}{xyz}+3\)
Lại có \(x+y+z=0\Leftrightarrow\left(x+y+z\right)\left(x^2+y^2+z^2-xy-yz-xz\right)=0\)
\(\Leftrightarrow x^3+y^3+z^3-3xyz=0\\ \Leftrightarrow x^3+y^3+z^3=3xyz\)
Thế vào \(P\)
\(\Leftrightarrow P=\dfrac{2\cdot3xyz}{xyz}+3=6+3=9\)
Chứng minh rằng:
a) (x+1)2>=4x
b) x2+y2+2>=2(x+y)
c) (1/x+1/y)(x+y)>=4 (với x>0; y>0)
d) x/y+y/x>=2 ( với x>0; y>0)
Giúp mình với ạ <3
a) Giả sử `(x+1)^2 >= 4x` là đúng.
Có: `(x+1)^2 >=4x <=> x^2+2x+1>=4x`
`<=>x^2+1>=2x`
`<=>x^2-2x+1>=0`
`<=> (x-1)^2>=0 forall x`.
Vậy điều giả sử là đúng.
b) `x^2+y^2+2 >=2(x+y)`
`<=> (x^2-2x+1)+(y^2-2y+1) >=0`
`<=>(x-1)^2+(y-1)^2>=0 forall x,y`
c) `(1/x+1/y)(x+y)>=4`
`<=> (x+y)/(xy) (x+y) >=4`
`<=> (x+y)^2 >= 4xy`
`<=> x^2+2xy+y^2>=4xy`
`<=> (x-y)^2>=0 forall x,y > 0`
d) `x/y+y/x>=2`
`<=> (x^2+y^2)/(xy) >=2`
`<=> x^2+y^2 >=2xy`
`<=> (x-y)^2>=0 \forall x,y>0`.
a) Xét hiệu \(\left(x+1\right)^2-4x\) = \(x^2-2x+1=\left(x-1\right)^2\ge0\)
=> \(\left(x+1\right)^2-\text{4x}\) \(\ge\) 0
=> \(\left(x+1\right)^2\ge\text{4x}\) (điều phải chứng minh)
b) xét hiệu \(x^2+y^2+2-2\left(x+y\right)\) = \(\left(x-1\right)^2+\left(y-1\right)^2\ge0\)
=> \(x^2+y^2+2-2\left(x+y\right)\ge0\)
=> \(x^2+y^2+2\ge2\left(x+y\right)\) (điều phải chứng minh)
c) Xét hiệu \(\left(\dfrac{1}{x}+\dfrac{1}{y}\right)\left(x+y\right)-4\) = \((\dfrac{x+y}{xy})\left(x+y\right)-4=\dfrac{\left(x+y\right)^2-4xy}{xy}=\dfrac{\left(x-y\right)^2}{xy}\) \(\ge0\)(vì x>0,y>0)
=>\(\left(\dfrac{1}{x}+\dfrac{1}{y}\right)\left(x+y\right)\ge4\) (điều phải chứng minh)
d) Áp dụng bất đẳng thức Cau-Chy cho các số x>0;y>0 ta có
\(\dfrac{x}{y}+\dfrac{y}{x}\ge2.\left(\dfrac{xy}{yx}\right)=2\)
=> \(\dfrac{x}{y}+\dfrac{y}{x}\ge2\) (điều phải chứng minh)
Mình làm hơi tắt mong bạn thông cảm nhé
Chúc bạn học tốt
Trong các cặp hình phẳng giới hạn bởi các đường sau, cặp nào có diện tích bằng nhau?
a) {y = x + sinx, y = x với 0 ≤ x ≤ π } và {y = x + sinx, y = x với π ≤ x ≤ 2 π }
b) {y = sinx, y = 0 với 0 ≤ x ≤ π } và {y = cosx, y = 0 với 0 ≤ x ≤ π };
c) {y = x , y = x 2 }
và { y = 1 - x 2 , y = 1 − x}
xy+x+y+1=0
xy-x-y=0
xy-x-y-1=0
xy-x-y+1=0
xy+2x+y+11=0
xy+x+y+1=0
xy-x-y=0
xy-x-y-1=0
xy-x-y+1=0
xy+2x+y+11=0
Hướng dẫn thôi nhé:
Lời giải:
a)\(xy+x+y+1=0\)
\(\Rightarrow x\left(y+1\right)+1\left(y+1\right)=0\)
\(\Rightarrow\left(x+1\right)\left(y+1\right)=0\)
b)\(xy-x-y=0\)
\(\Rightarrow xy-x-y+1=1\)
\(\Rightarrow x\left(y-1\right)-1\left(y-1\right)=1\)
\(\Rightarrow\left(x-1\right)\left(y-1\right)=1\)
c)\(xy-x-y-1=0\)
\(\Rightarrow xy-x-y+1=2\)
\(\Rightarrow x\left(y-1\right)-1\left(y-1\right)=2\)
\(\Rightarrow\left(x-1\right)\left(y-1\right)=2\)
d) \(xy-x-y+1=0\)
\(\Rightarrow x\left(y-1\right)-1\left(y-1\right)=0\)
\(\Rightarrow\left(x-1\right)\left(y-1\right)=0\)
e)\(xy+2x+y+11=0\)
\(\Rightarrow xy+2x+y+2=-9\)
\(\Rightarrow x\left(y+2\right)+1\left(y+2\right)=-9\)
\(\Rightarrow\left(x+1\right)\left(y+2\right)=-9\)