Các câu hỏi tương tự
Trong các cặp hình phẳng giới hạn bởi các đường sau, cặp nào có diện tích bằng nhau?a) {y x + sinx, y x với 0
≤
x
≤
π
} và {y x + sinx, y x với
π
≤
x
≤
2
π
}b) {y sinx, y 0 với 0
≤
x
≤
π
} và {y cosx, y 0 với 0
≤
x
≤
π
};c) {y ...
Đọc tiếp
Trong các cặp hình phẳng giới hạn bởi các đường sau, cặp nào có diện tích bằng nhau?
a) {y = x + sinx, y = x với 0 ≤ x ≤ π } và {y = x + sinx, y = x với π ≤ x ≤ 2 π }
b) {y = sinx, y = 0 với 0 ≤ x ≤ π } và {y = cosx, y = 0 với 0 ≤ x ≤ π };
c) {y = x , y = x 2 }
và { y = 1 - x 2 , y = 1 − x}
Hình phẳng (H) giới hạn bởi các đường
y
sin
x
,
y
cos
x
,
x
0
,
x
π
. Thể tích vật thể tạo thành khi quay (H) quanh trục hoành Ox bằng
Đọc tiếp
Hình phẳng (H) giới hạn bởi các đường y = sin x , y = cos x , x = 0 , x = π . Thể tích vật thể tạo thành khi quay (H) quanh trục hoành Ox bằng
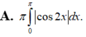
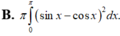
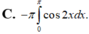
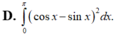
Diện tích của hình phẳng được giới hạn bởi các đường: y = tanx; y = 0; x = -π/4 và x = π/4 bằng:
A. π; B. -π;
C. ln2; D. 0
Diện tích của hình phẳng được giới hạn bởi các đường: y = tanx; y = 0; x = - π /4 và x = π /4 bằng:
A. π ; B. - π ;
C. ln2; D. 0
Tính thể tích của vật thể tròn xoay khi quay các hình phẳng giới hạn bởi các đường sau quanh trục Ox: y = 2x/ π ; y = sinx; x ∈ [0; π /2]
Cho hình phẳng (D) được giới hạn bởi các đường x0;
x
π
; y 0 và y -sinx. Thể tích V của khối tròn xoay tạo thành khi quay (D) xung quanh trục Ox được tính theo công thức:
Đọc tiếp
Cho hình phẳng (D) được giới hạn bởi các đường x=0; x = π ; y = 0 và y = -sinx. Thể tích V của khối tròn xoay tạo thành khi quay (D) xung quanh trục Ox được tính theo công thức:
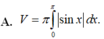
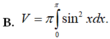
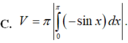
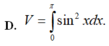
Cho hình phẳng (D) giới hạn bởi các đường
y
x
-
π
,
y
sinx
và
x
0
. Gọi V là thể tích khối tròn xoay tạo thành do (D) quay quanh trục hoành và
V
pπ
4
(
p
∈
Q
)
. Giá trị của 24p bằng A. 8 B. 4 C. 24 D. 12
Đọc tiếp
Cho hình phẳng (D) giới hạn bởi các đường y = x - π , y = sinx và x = 0 . Gọi V là thể tích khối tròn xoay tạo thành do (D) quay quanh trục hoành và V = pπ 4 ( p ∈ Q ) . Giá trị của 24p bằng
A. 8
B. 4
C. 24
D. 12
Cho hình phẳng D giới hạn bởi đường cong
y
2
+
sin
x
, trục hoành và các đường thẳng x 0;
x
π
. Khối tròn xoay tạo thành khi quay D quanh trục hoành có thể tích V bằng bao nhiêu ?
Đọc tiếp
Cho hình phẳng D giới hạn bởi đường cong y = 2 + sin x , trục hoành và các đường thẳng x = 0; x = π . Khối tròn xoay tạo thành khi quay D quanh trục hoành có thể tích V bằng bao nhiêu ?
![]()
![]()
![]()
![]()
Cho hình phẳng giới hạn bởi các đường y=√x và y=x quay xung quanh trục Ox. Thể tích của khối tròn xoay tạo thành bằng:
(A). 0
(B). –π
(C). π
(D). π/6
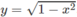 , y = 1 − x}
, y = 1 − x}
