Biết phương trình 2x+1. 5x = 15 có nghiệm duy nhất dạng alog5 + blog3 + clog2 với a; b; c nguyên . Tính S = a + 2b + 3c.
A. 2
B. 6
C. 4
D. 0
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
Biết rằng hệ phương trình m − 2 x − 3 y = − 5 x + m y = 3 có nghiệm duy nhất với mọi m. Tìm nghiệm duy nhất đó theo m.
A. x ; y = 9 + 5 m m 2 − 2 m + 3 ; 3 m + 1 m 2 − 2 m + 3
B. x ; y = 9 − 5 m m 2 − 2 m + 3 ; 3 m − 1 m 2 − 2 m + 3
C. x ; y = − 9 − 5 m m 2 − 2 m + 3 ; − 3 m − 1 m 2 − 2 m + 3
D. x ; y = 9 − 5 m m 2 − 2 m + 3 ; 3 m + 1 m 2 − 2 m + 3
Ta có:
m − 2 x − 3 y = − 5 x + m y = 3 ⇔ m − 2 3 − m y − 3 y = − 5 x = 3 − m y ⇔ 3 m − m 2 y − 6 + 2 m y − 3 y = − 5 x = 3 − m y ⇔ m 2 − 2 m + 3 y = 3 m − 1 1 x = 3 − m y 2
Ta có: m 2 – 2 m + 3 = ( m – 1 ) 2 + 2 > 0 ∀ m nên PT (1) có nghiệm duy nhất ∀ m
Hay hệ phương trình có nghiệm duy nhất ∀ m
Từ (1) ta có: y = 3 m − 1 m 2 − 2 m + 3 thay vào (2) ta có x = 9 − 5 m m 2 − 2 m + 3
Vậy x ; y = 9 − 5 m m 2 − 2 m + 3 ; 3 m − 1 m 2 − 2 m + 3
Đáp án: B
Biết rằng phương trình 2 + 5 x + 1 = 8 5 - 2 2 x - 1 có nghiệm duy nhất dạng log 2 + 5 a , với a là số thực dương. Mệnh đề nào dưới đây là đúng?
A. 0 < a < 4/5
B. 5 < a < 9
C. 4/5 < a < 12/5
D. 3 < a < 7/2
Chọn C.
Ta có: ![]() nên phương trình
nên phương trình 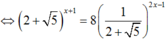
![]()
![]()
![]()
![]()
Do đó a = 2.
Biết rằng phương trình 2 2 x = 5 3 x + 1 có nghiệm duy nhất dạng a log 16 3 5 + log 16 3 3 với a ; b nguyên . Tính S = a +2b
A. 4
B. 3
C. 7
D. 6
Chọn A.
Phương trình ![]()
![]()
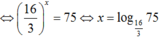 thỏa mãn (*)
thỏa mãn (*)
Ta có ![]()
Do đó: 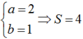
Cho phương trình m2 x+6(x +1 ) =m(5x + 3) (m là tham số) (1). Tìm m để phương trình (1) có một nghiệm duy nhất thỏa mãn biểu thức A= x2 + 2x + 3/x2 + 2 đạt giá trị nhỏ nhất
giúp e với ạ mai thi rồi cảm ơn !!!
Cho hệ phương trình:
\(\left\{{}\begin{matrix}2x+my=-5\\x-3y=2\end{matrix}\right.\)
a) Tìm m để hệ phương trình có nghiệm duy nhất, vô nghiệm, vô số nghiệm
b) Với giá trị nào của m thì hệ phương trình có nghiệm duy nhất thỏa mãn x+2y=1
`a,x-3y=2`
`<=>x=3y+2` ta thế vào phương trình trên:
`2(3y+2)+my=-5`
`<=>6y+4+my=-5`
`<=>y(m+6)=-9`
HPT có nghiệm duy nhất:
`<=>m+6 ne 0<=>m ne -6`
HPT vô số nghiệm
`<=>m+6=0,-6=0` vô lý `=>x in {cancel0}`
HPT vô nghiệm
`<=>m+6=0,-6 ne 0<=>m ne -6`
b,HPT có nghiệm duy nhất
`<=>m ne -6`(câu a)
`=>y=-9/(m+6)`
`<=>x=3y+2`
`<=>x=(-27+2m+12)/(m+6)`
`<=>x=(-15+2m)/(m+6)`
`x+2y=1`
`<=>(2m-15)/(m+6)+(-18)/(m+6)=1`
`<=>(2m-33)/(m+6)=1`
`2m-33=m+6`
`<=>m=39(TM)`
Vậy `m=39` thì HPT có nghiệm duy nhất `x+2y=1`
b)Ta có: \(\left\{{}\begin{matrix}2x+my=-5\\x-3y=2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=2+3y\\2\left(2+3y\right)+my=-5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2+3y\\6y+my+4=-5\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=3y+2\\y\left(m+6\right)=-9\end{matrix}\right.\)
Khi \(m\ne6\) thì \(y=-\dfrac{9}{m+6}\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=3y+2\\y=\dfrac{-9}{m+6}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=3\cdot\dfrac{-9}{m+6}+2\\y=-\dfrac{9}{m+6}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{-27}{m+6}+\dfrac{2m+12}{m+6}=\dfrac{2m-15}{m+6}\\y=\dfrac{-9}{m+6}\end{matrix}\right.\)
Để hệ phương trình có nghiệm duy nhất thỏa mãn x+2y=1 thì \(\dfrac{2m-15}{m+6}+\dfrac{-18}{m+6}=1\)
\(\Leftrightarrow2m-33=m+6\)
\(\Leftrightarrow2m-m=6+33\)
hay m=39
Vậy: Khi m=39 thì hệ phương trình có nghiệm duy nhất thỏa mãn x+2y=1
1/ Với giá trị nào của x thì 2 bất phương trình sau đây tương đương: (a-1)x - a+3>0 và ( a+1)x-a+2>0
2/ Bất phương trình: 5x/5 - 13/21 + x/15 < 9/25- 2x/35 có nghiệm là....
3/ Bất phương trình: 5x-1 < 2x/5 + 3 có nghiệm là...
4/ Bất phương trình: (x+4/x^2-9) -(2/x+3) < (4x/3x-x^2) có nghiệm nguyên lớn nhất là...
5/ Các nghiệm tự nhiên bé hơn 4 của bất phương trình (2x/5) -23 < 2x -16
6/ Các nghiệm tự nhiên bé hơn 6 của bất phương trình: 5x - 1/3 > 12 - 2x/3
7/ Bất phương trình: 2(x-1) - x > 3(x-1) - 2x-5 có tập nghiệm là...
8/ Bất phương trình: (3x+5/2) -1< (x+2/3)+x có tập nghiệm là...
9/ Bất phương trình: /x+2/ - /x-1/ < x - 3/2 có tập nghiệm là
10/ Bất phương trình: /x+1/ + /x-4/ > 7 có nghiệm nguyên dương nhỏ nhất là....
hoc gioi the hihiihihihhhihihihihiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiii
,mnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnn
Mình không biết sin lỗi vạn
Biết phương trình 2 x - 1 + x x 2 + 2 + x - 1 x 2 - 2 x + 3 = 0 có nghiệm duy nhất là a. Khi đó:
A. 0 < a < 1
B. 2 < a < 3
C. 3 < a < 4
D. 1 < a < 2
Cho hệ phương trình {4x-3y=6
{-5x+ay=8
a) Giải hệ phương trình với a=3
b) Tìm a để hệ phương trình có nghiệm âm duy nhất
a) Thay a=3 vào hệ pt, ta được:
\(\left\{{}\begin{matrix}4x-3y=6\\-5x+3y=8\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}-x=14\\4x-3y=6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-14\\-56-3y=6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-14\\-3y=62\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=-14\\y=-\dfrac{62}{3}\end{matrix}\right.\)
Vậy: Khi a=3 thì hệ pt có nghiệm duy nhất là: \(\left(x,y\right)=\left(-14;-\dfrac{62}{3}\right)\)
a. với a=3 ta có hpt: {4x-3y=6 {-5x+3y=8
<=> {-x=14 <=> {x=-14 {-5x+3y=8 {x= -62/3
Bài 4:
a) Tìm m để phương trình sau có nghiệm duy nhất: 2x - mx + 2m - 1 = 0.
b) Tìm m để phương trình sau có vô số nghiệm: mx + 4 = 2x + m2.
c) Tìm m để phương trình sau có nghiệm duy nhất dương: (m2 - 4)x + m - 2 = 0
à bài này a nhớ (hay mất điểm ở bài này) ;v
xinloi cậu tớ muốn giúp lắm mà tớ ngu toán:)
a)Ta có \(2x-mx+2m-1=0\\ =>x\left(2-m\right)+2m-1=0\)
Để pt có nghiệm duy nhất thì \(a\ne0=>2-m\ne0\\=>m\ne2\)
b)Ta có \(mx+4=2x+m^2\\ =>mx+4-2x+m^2=0\\ =>\left(m-2\right)x=m^2-4\)
Để pt vô số nghiệm thì \(\left\{{}\begin{matrix}m-2=0\\m^2-4=0\end{matrix}\right.=>\left\{{}\begin{matrix}m=2\\m=\pm2\end{matrix}\right.\)\(=>m=2\)
c)Để pt có nghiệm duy nhất thì \(m^2-4\ne0>m\ne\pm2\)
Chắc vậy :v