Vẽ đồ thị hàm số : a) y = - \(\dfrac{1}{2}\)x; b) y = 2x.
MT
Những câu hỏi liên quan
a) khảo sát và vẽ đồ thị hàm số \(y=\dfrac{2x-3}{x+2}\)
b) khảo sát và vẽ đồ thị hàm số \(y=\left|\dfrac{2x-3}{x+2}\right|\)
c) khảo sát và vẽ đồ thị hàm số \(y=\dfrac{2x-3}{\left|x+2\right|}\)
Vẽ đồ thị hàm số y=\(\dfrac{1}{2}.x\)
Các điểm sau đây có thuộc đồ thị hàm số A(2;3) B(2;1) C(1;2) D(3;1)
Cho hàm số y = (m+1) x+3 (1)
a) Tìm m để cho hàm số (1) là hàm số đồng biến, nghịch biến
b)Vẽ đồ thị (1) với m=1/2
c)Vẽ đồ thị (1) với m=-1\(\dfrac{1}{2}\)
bài1a) hãy xác định hàm số yax^2 bt rằng đồ thị của nó đi qua điểm M(-2;2) b) vẽ đồ thị hàm số y dfrac{1}{2}x^2bài 2 a)left{{}begin{matrix}4x+5y3x-3y5end{matrix}right. b) left{{}begin{matrix}dfrac{1}{x}+dfrac{1}{y}dfrac{4}{5}dfrac{1}{x}-dfrac{1}{y}dfrac{1}{5}end{matrix}right. giải hộ tui với
Đọc tiếp
bài1
a) hãy xác định hàm số y=ax\(^2\) bt rằng đồ thị của nó đi qua điểm \(M(-2;2)\)
b\()\) vẽ đồ thị hàm số y= \(\dfrac{1}{2}x^2\)
bài 2
a)\(\left\{{}\begin{matrix}4x+5y=3\\x-3y=5\end{matrix}\right.\)
b) \(\left\{{}\begin{matrix}\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{4}{5}\\\dfrac{1}{x}-\dfrac{1}{y}=\dfrac{1}{5}\end{matrix}\right.\)
giải hộ tui với ![]()
Bài 1:
a: Thay x=-2 và y=2 vào hàm số, ta được:
4a=2
hay a=1/2
Bài 2:
a: \(\Leftrightarrow\left\{{}\begin{matrix}4x+5y=3\\4x-12y=20\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}17y=-17\\x-3y=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-1\\3y=x-5=-6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-1\\y=-2\end{matrix}\right.\)
b: \(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{2}{x}=1\\\dfrac{1}{x}-\dfrac{1}{y}=\dfrac{1}{5}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\\dfrac{1}{y}=\dfrac{1}{2}-\dfrac{1}{5}=\dfrac{3}{10}\end{matrix}\right.\Leftrightarrow\left(x,y\right)=\left(2;\dfrac{10}{3}\right)\)
Đúng 2
Bình luận (0)
Cho 2 hàm số ydfrac{1}{2}x + 2 (d1) và y-2x + 2 (d2)a) Vẽ đồ thị của hai hàm số trên cùng một mặt phẳng tọa độb) Chứng tỏ điểm M(-5; -dfrac{1}{2}) thuộc đồ thị (d1) nhưng không thuộc đồ thị (d2)c) Gọi giao điểm của hai đường thẳng (d1) và (d2). Tìm tọa độ điểm S.d) Gọi giao điểm của hai đường thẳng (d1) và (d2) với trục hoành lần lượt là A và B. Tính chu vi và diện tích của tam giác SAB.e)Gọi OH là khoảng cách từ góc tọa độ O đến đường thẳng (d2). Tính OH
Đọc tiếp
Cho 2 hàm số y=\(\dfrac{1}{2}\)x + 2 (d1) và y=-2x + 2 (d2)
a) Vẽ đồ thị của hai hàm số trên cùng một mặt phẳng tọa độ
b) Chứng tỏ điểm M(-5; -\(\dfrac{1}{2}\)) thuộc đồ thị (d1) nhưng không thuộc đồ thị (d2)
c) Gọi giao điểm của hai đường thẳng (d1) và (d2). Tìm tọa độ điểm S.
d) Gọi giao điểm của hai đường thẳng (d1) và (d2) với trục hoành lần lượt là A và B. Tính chu vi và diện tích của tam giác SAB.
e)Gọi OH là khoảng cách từ góc tọa độ O đến đường thẳng (d2). Tính OH
a) Dựa vào đồ thị của hàm số ydfrac{1}{2}x^2�12�2(H.6.2), tìm x sao cho y8.b) Vẽ đồ thị của các hàm số y2x+1 và y2x^2 trên cùng một mặt phẳng tọa độ.
Đọc tiếp
a) Dựa vào đồ thị của hàm số \(y=\dfrac{1}{2}x^2\)(H.6.2), tìm \(x\) sao cho \(y=8\).
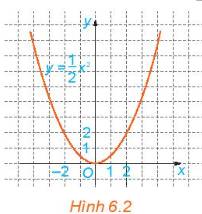
b) Vẽ đồ thị của các hàm số \(y=2x+1\) và \(y=2x^2\) trên cùng một mặt phẳng tọa độ.
a) Để \(y = 8 \Leftrightarrow \frac{1}{2}{x^2} = 8 \Leftrightarrow {x^2} = 16 \Leftrightarrow x = 4\) hoăc \(x = - 4\)
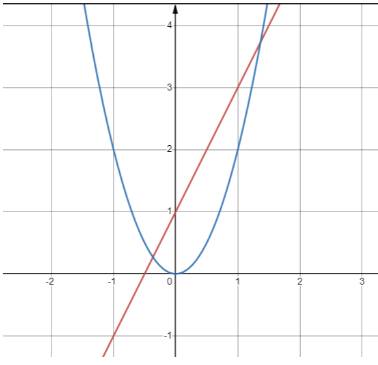
b) Vẽ đồ thị y=2x+1:
-Là đồ thị bậc nhất nên đồ thị là đường thẳng đi qua điểm có tọa độ (0; 1) và
(-1; -1)
Vẽ đồ thị \(y = 2{x^2}\)
- Đi qua điểm (1; 2) ; (-1; 2);(0;0)
Đúng 0
Bình luận (0)
Cho hàm số \(y=\dfrac{1}{2}x^2\) có đồ thị thì (P) và đường thẳng (d) có phương trình: \(y=x+1\)
a, Vẽ đồ thị hai hàm số trên cùng một mặt phẳng tọa độ Oxy
b, Tìm tọa độ giao điểm của 2 hàm số trên.
không vẽ đồ thị hãy tìm tọa độ các giao điểm của các đồ thị hàm số sau:
a) y=x\(^2\)và y=\(\dfrac{1}{2}\)x b) y=\(-\dfrac{1}{2}x^2\)và y=mx+\(\dfrac{1}{2}m^2-8\)
a, Hoành độ giao điểm tm pt
\(x^2-\dfrac{1}{2}x=0\Leftrightarrow x\left(x-\dfrac{1}{2}\right)=0\Leftrightarrow x=0;x=\dfrac{1}{2}\)
Với x = 0 => y = 0
Với x = 1/2 => y = 1/4
Vậy (P) cắt (d) tại O(0;0) ; A(1/2;1/4)
Đúng 0
Bình luận (0)
Cho hàm số y = ax2a) Xác định a để đồ thị của hàm số trên đi qua điểm A (4 ; 4).
b) Vẽ đồ thị của hàm số trên với a vừa tìm được và đồ thị của hàm số y = \(-\dfrac{1}{2}x\) trên cùng một mặt phẳng tọa độ Oxy.
c) Tìm tọa độ giao điểm của hai hàm số trên (câu b) bằng phép toán.
a) Để đồ thị hàm số \(y=ax^2\) đi qua điểm A(4;4) thì
Thay x=4 và y=4 vào hàm số \(y=ax^2\), ta được:
\(a\cdot4^2=4\)
\(\Leftrightarrow a\cdot16=4\)
hay \(a=\dfrac{1}{4}\)
Đúng 2
Bình luận (0)
a, - Thay tọa độ điểm A vào hàm số ta được : \(4^2.a=4\)
\(\Rightarrow a=\dfrac{1}{4}\)
b, Thay a vào hàm số ta được : \(y=\dfrac{1}{4}x^2\)
- Ta có đồ thì của hai hàm số :
c, - Xét phương trình hoành độ giao điểm :\(\dfrac{1}{4}x^2=-\dfrac{1}{2}x\)
\(\Leftrightarrow x^2+2x=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-2\end{matrix}\right.\)
Vậy hai hàm số trên cắt nhau tại hai điểm : \(\left(0;0\right);\left(-2;1\right)\)
Đúng 1
Bình luận (0)




