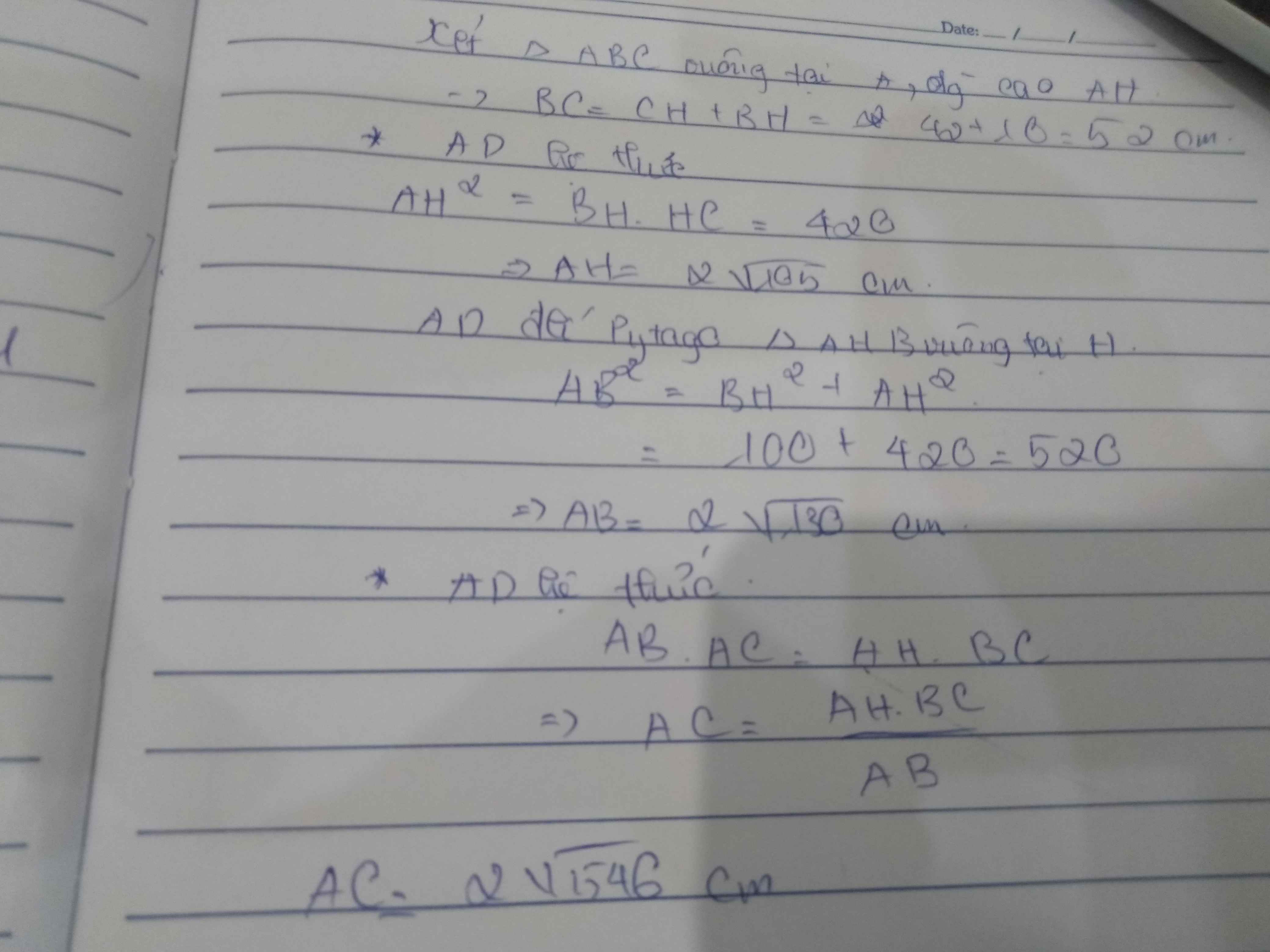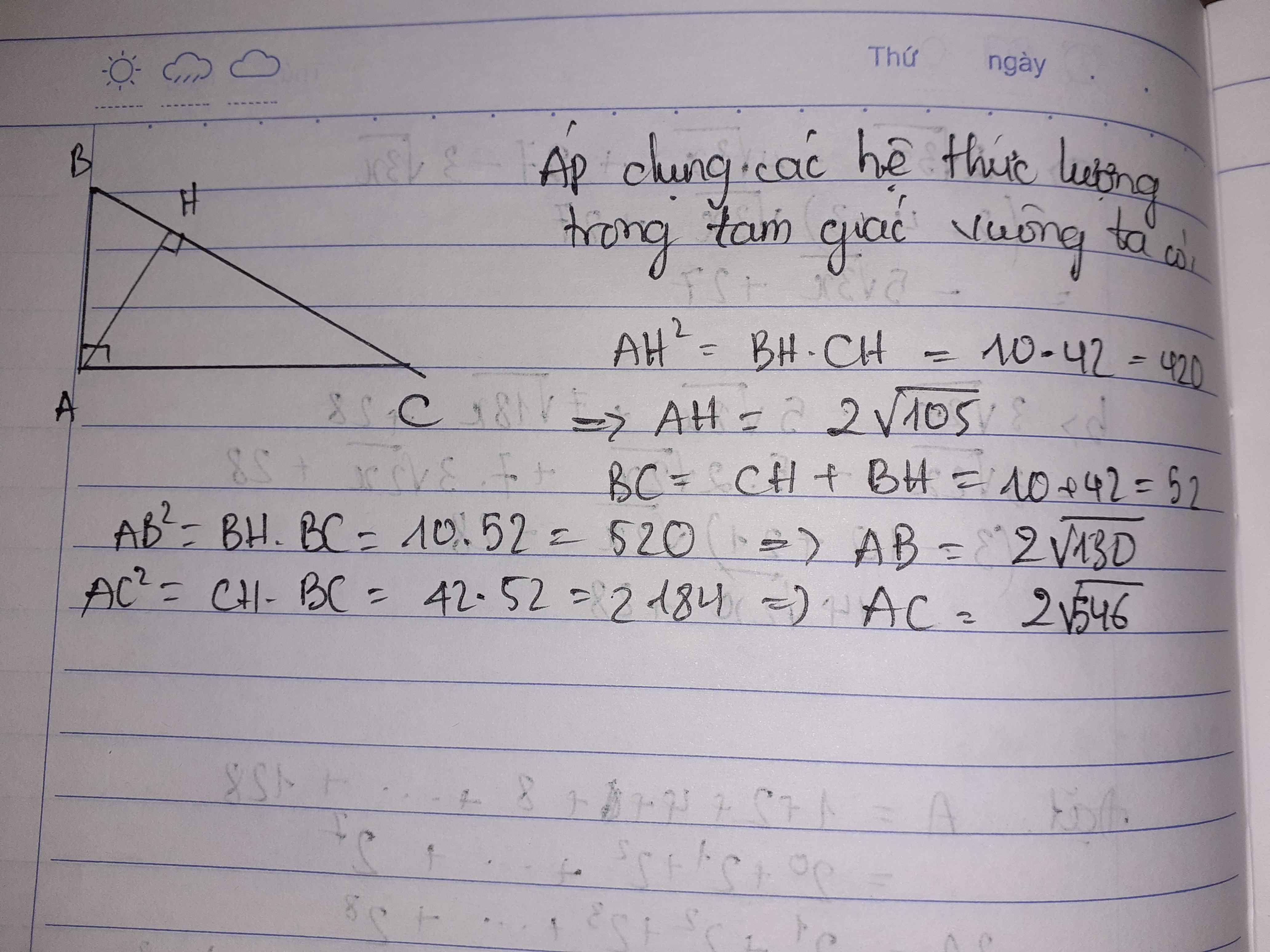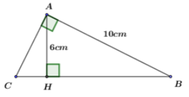
Áp dụng định lý Pytago trong tam giác ABH vuông tại H. Ta có:

Trong tam giác vuông ABC vuông tại A có AH là đường cao

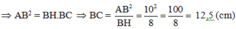
Áp dụng định lý Py-ta-go cho tam giác vuông ABC ta có:

Vậy AC = 7,5 (cm); BC =  12,5 (cm)

Đáp án cần chọn là: B

a: AC=8cm

b: \(S_{ABC}=\dfrac{AB\cdot AC}{2}=\dfrac{6\cdot8}{2}=24\left(cm^2\right)\)

c: AH=4,8cm

AH=6*8/10=4,8cm

\(BC=BH+CH=52\left(cm\right)\)

\(AH=\sqrt{BH.CH}=2\sqrt{105}\) (cm)

\(AB^2=BH.BC\Rightarrow AB=\sqrt{BH.BC}=2\sqrt{130}\left(cm\right)\)

\(AC^2=CH.BC\Rightarrow AC=\sqrt{CH.BC}=2\sqrt{546}\left(cm\right)\)

Ta có: BC=BH+CH(H nằm giữa B và C)

nên BC=10+42=52(cm)

Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:

\(AH^2=HB\cdot HC\)
\(\Leftrightarrow AH^2=10\cdot42=420\)

hay \(AH=2\sqrt{105}\left(cm\right)\)

Áp dụng định lí Pytago vào ΔABH vuông tại H, ta được:

\(AB^2=AH^2+BH^2\)

\(\Leftrightarrow AB^2=\left(2\sqrt{105}\right)^2+10^2=420+100=520\)

hay \(AB=2\sqrt{130}\left(cm\right)\)

Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:

\(BC^2=AB^2+AC^2\)

\(\Leftrightarrow AC^2=BC^2-AB^2=52^2-520=2184\)

hay \(AC=2\sqrt{546}\left(cm\right)\)

Xét tam giác ABC vuông ta có: 

\(BC=\sqrt{AB^2+AC^2}=\sqrt{24^2+10^2}=26\left(cm\right)\)

\(\left\{{}\begin{matrix}BH=\dfrac{AB^2}{BC}=\dfrac{10^2}{26}\approx4\left(cm\right)\\HC=\dfrac{AC^2}{BC}=\dfrac{24^2}{26}\approx22\left(cm\right)\end{matrix}\right.\)

Xét tam giác ABH vuông tại H áp dung Py-ta-go ta có: 

\(\Rightarrow AH=\sqrt{AB^2-BH^2}=\sqrt{10^2-4^2}=2\sqrt{21}\left(cm\right)\)

\(\Rightarrow S_{ABC}=\dfrac{1}{2}\cdot AH\cdot BC=\dfrac{1}{2}\cdot2\sqrt{21}\cdot26=26\sqrt{21}\left(cm^2\right)\)

Ta có :

\(BC^2=AB^2+AC^2\left(Pitago\right)\)

\(\Leftrightarrow BC^2=100+576=676\)

\(\Leftrightarrow BC=26\left(cm\right)\)

\(AB^2=BH.BC\Leftrightarrow BH=\dfrac{AB^2}{BC}=\dfrac{100}{26}=\dfrac{50}{13}\left(cm\right)\)

\(BC=BH-HC\)

\(\Leftrightarrow HC=BC-BH=26-\dfrac{50}{13}=\dfrac{288}{13}\left(cm\right)\)

\(AH^2=BH.HC=\dfrac{50}{13}.\dfrac{288}{13}=\dfrac{14400}{13^2}\)

\(\Leftrightarrow AH=\dfrac{120}{13}\left(cm\right)\)

\(S_{ABC}=\dfrac{1}{2}.AB.AC=\dfrac{1}{2}.10.24=120\left(cm^2\right)\)

Hoặc : \(S_{ABC}=\dfrac{1}{2}.AH.BC=\dfrac{1}{2}.\dfrac{120}{13}.26=120\left(cm^2\right)\)

a: Xét ΔAHB vuông tại H và ΔAHC vuông tại H có

AB=AC

AH chung

Do đó: ΔAHB=ΔAHC

b: AH=8cm

nên CH=6cm

=>BC=12cm

 BÀI 1:

a)

·         Trong ∆ ABC, có:     AB²= BC.BH

                           Hay BC= =

·         Xét ∆ ABC vuông tại A, có:

    AB²= BH²+AH²

↔AH²= AB² – BH²

↔AH= =4 (cm)

b)

·         Ta có: HC=BC-BH

      àHC= 8.3 - 3= 5.3 (cm)

·         Trong ∆ AHC, có:    

·                                         

Bài 1:

a)  Áp dụng hệ thức lượng ta có:

   \(AB^2=BH.BC\)

\(\Rightarrow\)\(BC=\frac{AB^2}{BH}\)

\(\Rightarrow\)\(BC=\frac{5^2}{3}=\frac{25}{3}\)

Áp dụng Pytago ta có:

     \(AH^2+BH^2=AB^2\)

\(\Rightarrow\)\(AH^2=AB^2-BH^2\)

\(\Rightarrow\)\(AH^2=5^2-3^2=16\)

\(\Rightarrow\)\(AH=4\)

b)  \(HC=BC-BH=\frac{25}{3}-3=\frac{16}{3}\)

Áp dụng hệ thức lượng ta có:

   \(\frac{1}{HE^2}=\frac{1}{AH^2}+\frac{1}{HC^2}\)

\(\Leftrightarrow\)\(\frac{1}{HE^2}=\frac{1}{4^2}+\frac{1}{\left(\frac{16}{3}\right)^2}=\frac{25}{256}\)

\(\Rightarrow\)\(\frac{1}{HE}=\frac{5}{16}\)

\(\Rightarrow\)\(HE=\frac{16}{5}\)

Ta có: BC=BH+CH

nên BC=10+42=52cm

Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được: 

\(\left\{{}\begin{matrix}AH^2=HB\cdot HC\\AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AH=2\sqrt{105}cm\\AB=2\sqrt{130}cm\\AC=2\sqrt{546}cm\end{matrix}\right.\)