Cho tam giác ABC : BE là phân giác của góc ABC ; CF là phân giác của ACB . Gọi I là giao điểm của BE và CF
Chứng minh rằng Góc BIC = 90 độ + góc BAC : 2
Cho tam giác ABC, tia phân giác BE VÀ CD LẦN LƯỢT LÀ CÁC TIA PHÂN GIÁC CỦA GÓC B,C(E THUỘC AC,D THUỘC AB) SAO CHO BE=CD. CM: TAM GIÁC ABC LÀ TAM GIÁC CÂN
Cho tam giác ABC có A=90 độ,góc ABC=60 độ,BE là phân giác của góc ABC trên tia đối cuẩE lấy D sao cho AD=AE a.chứng minh:tam giác ABD=tam giác ABE và tam giác BDE đều b)BE=BC c)BD vuông góc BC
a: Xét ΔABD vuông tại A và ΔABE vuông tại A có
AB chung
AD=AE
=>ΔABD=ΔABE
=>BD=BE
=>ΔBED cân tại B
mà góc BED=60 độ
nên ΔBED đều
c: góc DBC=góc DBA+góc CBA
=30+60=90 độ
=>BD vuông góc BC
b: Sửa đề: Cm EB=EC
Xét ΔEBC có góc EBC=góc ECB
nên ΔEBC cân tại E
=>EB=EC
cho tam giác ABC, có AB = AC, kẻ bE vuông góc với AC, CD vuông góc với AB. Gọi O là giao điểm của BE và CD. CMR : a) tam giác ABC = tam giác AEB, b) AO là phân giác của BAC
a: Xét ΔAEB vuông tại E và ΔADC vuông tại D có
AB=AC
\(\widehat{A}\) chung
Do đó: ΔAEB=ΔADC
Cho tam giác ABC và hai phân giác BE, CF. Biết EF là tia phân giác của góc AEB. TÍnh số đo góc ABC.
Cho tam giác ABC vuông tại A, BA = BE. BD là tia phân giác của góc ABC, AH vuông góc với BC. Chứng minh:
a, Tam giác ABD = tam giác EBD
b, AH // DE
Sửa đề:
Cho tam giác ABC vuông tại A. Trên cạnh BC lấy điểm E sao cho BA = BE. BD là tia phân giác của góc ABC, AH vuông góc với BC. Chứng minh:
a, Tam giác ABD = tam giác EBD
b, AH // DE
Giải
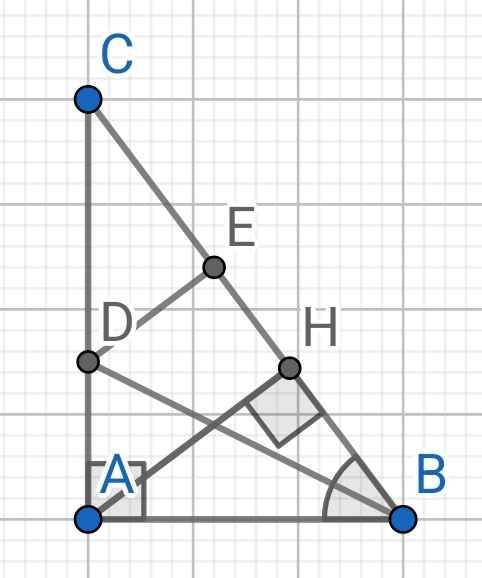 a) Do BD là tia phân giác của ∠ABC (gt)
a) Do BD là tia phân giác của ∠ABC (gt)
⇒ ∠ABD = ∠CBD
⇒ ∠ABD = ∠EBD
Xét ∆ABD và ∆EBD có:
BD là cạnh chung
∠ABD = ∠EBD (cmt)
BA = BE (gt)
⇒ ∆ABD = ∆EBD (c-g-c)
b) Do ∆ABD = ∆EBD (cmt)
⇒ ∠BAD = ∠BED (hai góc tương ứng)
⇒ ∠BED = 90⁰
⇒ DE ⊥ BC
Mà AH ⊥ BC (gt)
⇒ AH // DE
Để chứng minh a, ta cần chứng minh hai tam giác ABD và EBD có cạnh và góc tương ứng bằng nhau.
Vì tam giác ABC vuông tại A, nên ta có góc ABC = 90 độ. Vì BD là tia phân giác của góc ABC, nên ta có góc ABD = góc DBC.
Vì BA = BE, và góc ABD = góc DBC, nên ta có hai cạnh và góc tương ứng bằng nhau, theo nguyên tắc cạnh-góc-cạnh (SAS), ta có tam giác ABD = tam giác EBD.
Để chứng minh b, ta cần chứng minh hai đường thẳng AH và DE là song song.
Vì tam giác ABC vuông tại A, nên ta có góc ABC = 90 độ. Vì BD là tia phân giác của góc ABC, nên ta có góc ABD = góc DBC.
Vì tam giác ABD = tam giác EBD (đã chứng minh ở câu a), nên ta có góc ADB = góc EDB.
Vì góc ADB = góc EDB và góc ABD = góc DBC, nên theo nguyên tắc góc tương đương, ta có AH // DE.
Vậy, ta đã chứng minh được cả hai phần a và b.
Cho tam giác ABC cân tại A có AD,BE là đường phân giác.Tính các góc của tam giác ABC khi BE=2AD
Help:
cho tam giác ABC có 2 phân giác BE và CF, biết EF là phân giác của góc aeb. tính số đo góc ABC
cho tam giác ABC vẽ phân giác BE Và CF của tam giác abc gọi o là điểm cách đều 3 cạnh của tam giác.tính góc A của tam giác ABC pit điểm đới xứng của F qua BE cx là điểm đối xứng của E qua CF
cho tam giác ABC(AC>AB), tia phân giác của góc BAC cắt BC tại D. Trên cạnh AC lấy điểm E sao cho AE=AB. Nối D với E.C/m tam giác ABD=AED,AD vuông góc BE,gọi Ax là tia phân giác của góc ngoài ở đỉnh A của tam giác ABC,C/m Ax // BE, tìm điều kiện của tam giác ABC để DE vuông góc với AC
Giúp mik vs mai kt