Bài 8: Cho hình thang ABCD vuông (AB//CD, A = 900) Có AB = 2cm; CD = 4cm, C =300 , kẻ BH vuông góc với CD tại H.
Tính HD; CH; BH; BC?
giúp e vs ạ:(
Bài 8: Cho hình thang ABCD vuông (AB//CD, A = 900) Có AB = 2cm; CD = 4cm, C =300 , kẻ BH vuông góc với CD tại H.
Tính HD; CH; BH; BC?
Cho hình thang vuông ABCD A ^ = D ^ = 90 0 , trong đó có C ^ = 45 0 , AB = 2cm, CD = 4cm. Diện tích của hình thang vuông ABCD là
A. 3 c m 2
B. 8 c m 2
C. 4 c m 2
D. 6 c m 2
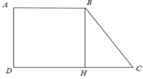
Xét hình thang ABCD
Từ B kẻ BH ⊥ CD, khi đó ta được hình chữ nhật ABHD ⇒ AB = DH = 2cm
⇒ HC = CD - DH = 4 - 2 = 2cm.
+ Xét Δ BDC có BH là đường cao đồng thời là đường trung tuyến
⇒ Δ BDC là tam giác cân tại B.

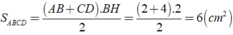
Chọn đáp án D.
Cho hình thang vuông ABCD A ^ = D ^ = 90 0 , trong đó có C ^ = 45 0 , AB = 2cm, CD = 4cm. Diện tích của hình thang vuông ABCD là
A. 3 c m 2
B. 8 c m 2
C. 4 c m 2
D. 6 c m 2
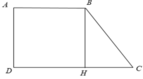
Xét hình thang ABCD
Từ B kẻ BH ⊥ CD, khi đó ta được hình chữ nhật ABHD ⇒ AB = DH = 2cm
⇒ HC = CD - DH = 4 - 2 = 2cm.
+ Xét Δ BDC có BH là đường cao đồng thời là đường trung tuyến
⇒ Δ BDC là tam giác cân tại B.

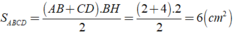
Chọn đáp án D.
Hình thang vuông ABCD có ∠ A = ∠ D = 90 0 , AB = AD = 2cm, DC = 4cm. Tính các góc của hình thang.
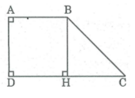
Kẻ BH ⊥ CD
Ta có: AD ⊥ CD ( Vì ABCD là hình thang vuông có ∠ A = ∠ D = 90 0 )
Suy ra: BH // AD
Hình thang ABHD có hai cạnh bên song song nên HD = AB và BH = AD
AB = AD = 2cm (gt)
⇒ BH = HD = 2cm
CH = CD – HD = 4 – 2 = 2 (cm)
Suy ra: ∆ BHC vuông cân tại H
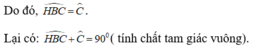
⇒ ∠ C = 45 0
∠ B + ∠ C = 180 0 (2 góc trong cùng phía bù nhau) ⇒ ∠ B = 180 0 – 45 0 = 135 0
Bài 3: Cho hình thang ABCD (đáy AB, CD) 𝐴̂ = 𝐷̂ = 900 có hai đường chéo vuông góc với nhau tại O, AB = 15cm, AD = 20cm.
a) Tính độ dài OB, OD
b) Tính độ dài AC
c) Tính diện tích hình thang ABCD
a: Xét ΔDAB vuông tại A có
\(DB^2=AB^2+AD^2\)
hay DB=25(cm)
Xét ΔDAB vuông tại A có AO là đường cao ứng với cạnh huyền DB
nên \(\left\{{}\begin{matrix}AD^2=DO\cdot DB\\AB^2=BO\cdot BD\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}DO=16\left(cm\right)\\OB=9\left(cm\right)\end{matrix}\right.\)
\(a,BD=\sqrt{AB^2+AD^2}=25\left(cm\right)\left(pytago\right)\)
Áp dụng HTL:
\(\left\{{}\begin{matrix}AD^2=OD\cdot BD\\AB^2=OB\cdot BD\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}OD=\dfrac{AD^2}{BD}=16\left(cm\right)\\OB=\dfrac{AB^2}{BD}=9\left(cm\right)\end{matrix}\right.\)
\(b,\) Áp dụng HTL:
\(\left\{{}\begin{matrix}AO^2=DO\cdot OB=144\\AD^2=AO\cdot AC\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}AO=12\left(cm\right)\\AC=\dfrac{AD^2}{AO}=\dfrac{100}{3}\left(cm\right)\end{matrix}\right.\)
\(c,DC=\sqrt{AD^2+AC^2}=\dfrac{20\sqrt{34}}{3}\left(cm\right)\\ S_{ABCD}=\dfrac{1}{2}AD\left(AB+CD\right)=10\left(\dfrac{20\sqrt{34}}{3}+15\right)=\dfrac{450+200\sqrt{34}}{3}\left(cm^2\right)\)
Cho hình thang cân ABCD (AB//CD) có AC vuông góc với BD tại O.
a) Chứng minh các tam giác OCD, OAB vuông cân.
b) Biết AB = 2cm, CD = 8cm, AD = 5cm. Tính diện tích hình thang ABCD.
. a) HS tự chứng minh
b) Kẻ đường cao AH, BK,chứng minh được DH = CK
Ta được H D = C D − A B 2 = 3 c m
Þ AH = 4cm Þ SABCD = 20cm2
Bài 8: cho hình thang vuông ABCD có góc A = góc D = 90o . AB = AD = 2cm, DC = 4cm. Tính hai góc còn lại của hình thang
Cho một hình thang vuông ABCD , có góc A=D=90độ, AB=AD=2cm,CD=4cm.Tính gócB,C của hình thang
Trường Huỳnh Đoàn
căn bậc 2 của 8 ( cm)
ai thấy đúng thì k nha