Tứ giác ABCD có AD = BC; AC = BD. CMR :ABCD là hình thang cân
NT
Những câu hỏi liên quan
1/Cho tứ giác ABCD có AB//CD,AD//BC.Chứng minh AD=BC,AB=CD.
2/Cho tứ giác ABCD có AB//CD,AB=CD.Chứng minh AD//BC và AD=BC
1/nối AC
Do AB//CD=>BAC=ACD(so le trong)
Do AD//BC=>ACB=DAC(so le trong)
Xét ∆ABC và ∆ACD
ACB=DAC(chứng minh trên)
BAC=DAC(chứng minh trên)
AC chung
Vậy ∆ABC=∆CDA(g.c.g)=>AB=DC(cặp cạnh tương ứng)
AD=BC(cặp cạnh tương ứng)
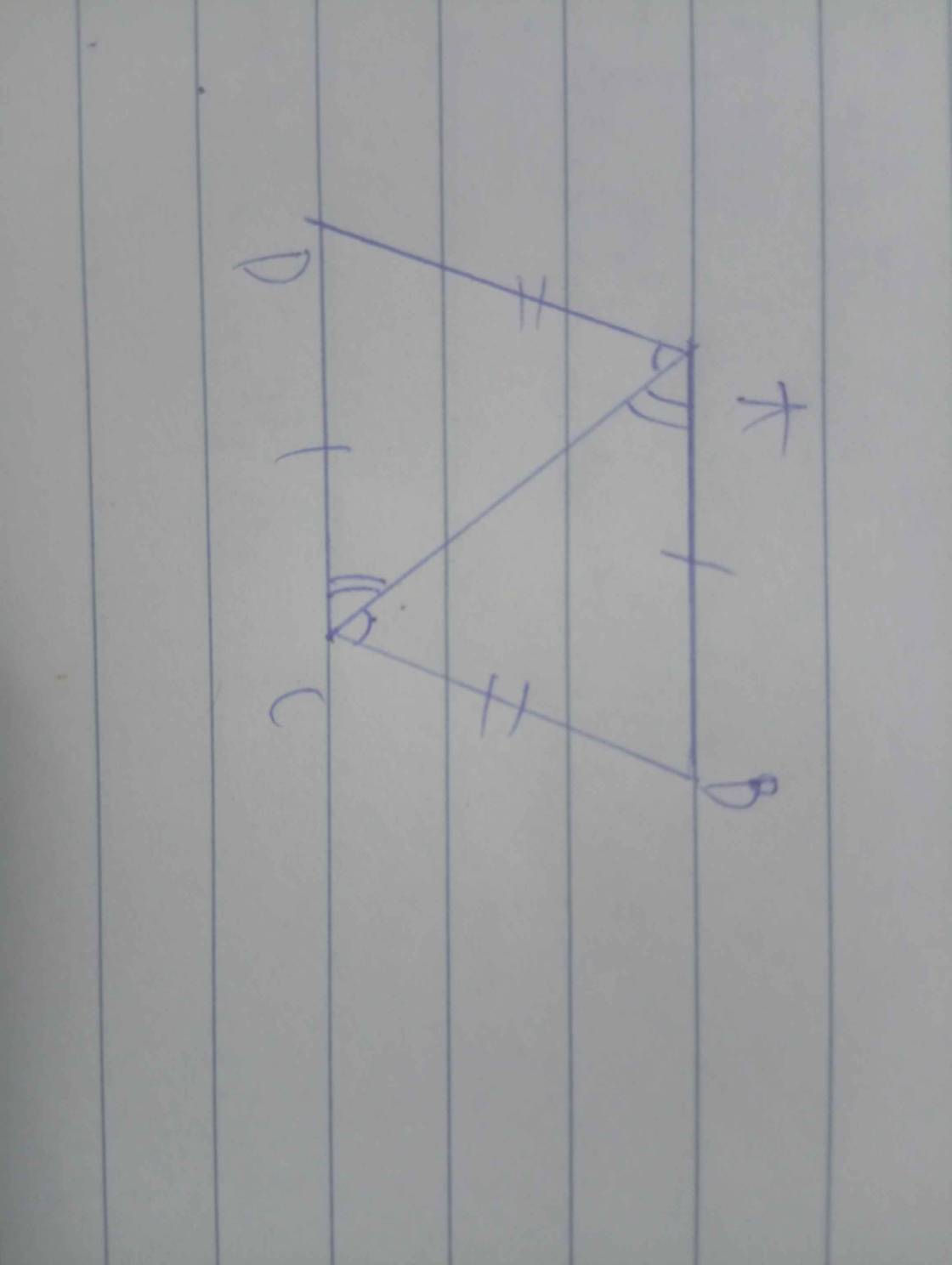
Đúng 0
Bình luận (0)
Câu 17:. Chọn câu đúng:A. Tứ giác ABCD là hình chữ nhật khi có và . B. Tứ giác ABCD là hình chữ nhật khi có và . C. Tứ giác ABCD là hình chữ nhật khi có ABCD; ADBC; ACBD. D. Tứ giác ABCD là hình chữ nhật khi có ABCD; ABBC và ACBD.
Đọc tiếp
Câu 17:. Chọn câu đúng:
A. Tứ giác ABCD là hình chữ nhật khi có và
.
B. Tứ giác ABCD là hình chữ nhật khi có và
.
C. Tứ giác ABCD là hình chữ nhật khi có AB=CD; AD=BC; AC=BD.
D. Tứ giác ABCD là hình chữ nhật khi có AB=CD; AB=BC và AC=BD.
Cho tứ giác ABCD có góc A= góc B, AD=BC. Chứng minh tứ giác ABCD là hình thang cân
Xét ΔADB và ΔBCA có
AD=BC
\(\widehat{DAB}=\widehat{CBA}\)
AB chung
Do đó: ΔADB=ΔBCA
Suy ra: DB=CA
Xét ΔACD và ΔBDC có
AC=BD
DC chung
AD=BC
Do đó: ΔACD=ΔBDC
Suy ra: \(\widehat{ADC}=\widehat{BCD}\)
Xét tứ giác ABCD có
\(\widehat{DAB}+\widehat{ABC}+\widehat{ADC}+\widehat{BCD}=360^0\)
\(\Leftrightarrow2\cdot\left(\widehat{DAB}+\widehat{ADC}\right)=360^0\)
\(\Leftrightarrow\widehat{DAB}+\widehat{ADC}=180^0\)
mà hai góc này là hai góc ở vị trí trong cùng phía
nên AB//CD
Xét tứ giác ABCD có AB//CD
nên ABCD là hình thang
mà AC=BD
nên ABCD là hình thang cân
Đúng 0
Bình luận (0)
Cho tứ giác ABCD có góc A bằng góc B; BC = AD. CMR: tứ giác ABCD là hình thang cân.
Cho tứ giác ABCD, có AB // CD, AD // với BC. Chứng minh AB=CD, AD=BC
Xét tứ giác ABCD có
AB//CD
AD//BC
DO đó: ABCD là hình bình hành
Suy ra: AB=CD; AD=BC
Đúng 1
Bình luận (0)
Xét tứ giác ABCD có:
AD//BC
AB//CD
Suy ra: Tứ giác ABCD là hình bình hành vì có 2 cặp cạnh song song
Suy ra: AB=CD; AD=BC
Đúng 1
Bình luận (0)
cho tứ giác abcd có ab//cd, ad//bc cm ab = cd , ad-= bc
Cho tứ giác ABCD có: AB=5cm; AB+BC=12cm; BC+CD=12cm; CD+AD=12cm. CM: tứ giác ABCD là hình bình hành
helpp
AB = 5cm
=> BC = 12 - 5 = 7cm
=> CD = 12 - 7 = 5cm
=> AD = 12 - 5 = 7cm
Vì AB = CD, BC = AD, mà AB đối CD, BC đối AD
=> Tứ giác ABCD là hbh
Đúng 0
Bình luận (0)
b2. Nếu tứ giác ABCD có M,N là trung điểm của AD, BC và MN =1/2(AB+CD). Vậy tứ giác ABCD là tứ giác đặc biệt gì?
Tứ giác abcd có ad=bc ,ac là tia phân giác của a cmr abcd là hình thang
Xem chi tiết
Sửa đề: AB=BC
Xét ΔABC có BA=BC(gt)
nên ΔBAC cân tại B(Định nghĩa tam giác cân)
⇒\(\widehat{BAC}=\widehat{BCA}\)(hai góc ở đáy)
mà \(\widehat{BAC}=\widehat{DAC}\)(AC là tia phân giác của \(\widehat{BAD}\))
nên \(\widehat{BCA}=\widehat{DAC}\)
mà \(\widehat{BCA}\) và \(\widehat{DAC}\) là hai góc ở vị trí so le trong
nên AD//BC(Dấu hiệu nhận biết hai đường thẳng song song)
Xét tứ giác ABCD có AD//BC(cmt)
nên ABCD là hình thang có hai đáy là AD và BC(Định nghĩa hình thang)
Đúng 0
Bình luận (0)
tứ giác ABCD có C=A và BC//AD. chứng minh rằng tứ giác đó là hình bình hành.
BC//AD nên \(\widehat{A}+\widehat{B}=180^0;\widehat{C}+\widehat{D}=180^0\)
Mà \(\widehat{A}=\widehat{C}\Rightarrow\widehat{B}=\widehat{D}\)
Vậy ABCD là hbh
Đúng 0
Bình luận (1)




