Cho tam giác ABC góc A = 900 ; AB=3 cm; AC=4cm
a) Tính BC, góc B, góc C
b)Phân giác của góc A cắt BC tại E. Tính BE, CE
c)Từ E kẻ EM,EN lần lượt vuông góc với AB, AC
Hỏi tứ giác AMEN là hình gì?
Tính chu vi và diện tích của tứ giác AMEN?
BH
Những câu hỏi liên quan
Cho tam giác ABC có góc B và góc C nhỏ hơn 900 . Vẽ ra phía ngoài tam giác ấy các tam giác vuông cân ABD và ACE ( trong đó góc ABD và góc ACE đều bằng 900 ), vẽ DI và EK cùng vuông góc với đường thẳng BC. AH là đường cao của tam giác ABC. Chứng minh rằng: a. BI=AH; EK = HC; b. BC = DI + EK.
Xem chi tiết
Cho tam giác ABC và tam giác MNP có
A
^
M
^
90
0
,
C
^
P
^
. Cần điều kiện gì để hai tam giác ABC và tam giác MNP bằng nhau theo trường hợp cạnh góc vuông – góc nhọn kề? A.
A
C
M
P
B.
A
B
M
N
C.
B
C...
Đọc tiếp
Cho tam giác ABC và tam giác MNP có A ^ = M ^ = 90 0 , C ^ = P ^ . Cần điều kiện gì để hai tam giác ABC và tam giác MNP bằng nhau theo trường hợp cạnh góc vuông – góc nhọn kề?
A. A C = M P
B. A B = M N
C. B C = N P
D. A C = M N
Ta có: C ^ = P ^ mà góc C và góc P là hai góc nhọn kề của tam giác ABC và tam giác MNP
Do đó để tam giác ABC và tam giác MNP bằng nhau theo trường hợp cạnh góc vuông – góc nhọn kề thì cần thêm điều kiện A C = M P
Đáp án A
Đúng 0
Bình luận (0)
Cho tam giác ABC có góc B và góc C nhỏ hơn 900 . Vẽ ra phía ngoài tam giác ấy các tam giác vuông cân ABD và ACE ( trong đó góc ABD và góc ACE đều bằng 900 ), vẽ DI và EK cùng vuông góc với đường thẳng BC. AH là đường cao của tam giác ABC. Chứng minh rằng: a. BI=AH; EK = HC; b. BC = DI + EK.:
Cho tam giác ABC, có góc A = 900 . Tia phân giác BE của góc ABC ( E AC ). Trên BC lấy M sao cho BM=BA. a) Chứng minh BEA BEM b) Chứng minh EM BC c) So sánh góc ABC và góc MEC
Cho tam giác ABC, góc A = 900, AH vuông góc BC, AB = 6cm, AC = 8 cm, phân giác của góc B cắt AH tại I, cắt BC tại D
1. Tính BC, AD, DC
2. CM tam giác ABC đồng dạng với tam giác HBA, tam giác ABI đồng dạng với tam giác CBD
3. CM AB2 = BH . BC, AH2 = HB . HC, \(\dfrac{IH}{IA}\) = \(\dfrac{AD}{BC}\)
1: BC=10cm
Xét ΔABC có BD là đường phân giác
nên AD/AB=DC/BC
=>AD/6=DC/10
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{AD}{6}=\dfrac{CD}{10}=\dfrac{AD+CD}{6+10}=\dfrac{8}{16}=\dfrac{1}{2}\)
Do đó: AD=3(cm); BD=5(cm)
2: Xét ΔABC vuông tại A và ΔHBA vuông tại H có
\(\widehat{B}\) chung
Do đó: ΔABC\(\sim\)ΔHBA
Xét ΔABI và ΔCBD có
\(\widehat{ABI}=\widehat{CBD}\)
\(\widehat{IAB}=\widehat{DCB}\)
Do đó: ΔABI\(\sim\)ΔCBD
Đúng 1
Bình luận (0)
Bài 5: Cho tam giác ABC có A = 900 ; 2B = 7C. a) Tính số đo góc B; C b) Kẻ AD là tia phân giác của góc A. Tính góc ADC
a) Ta có: \(2\widehat{B}=7\widehat{C}\Rightarrow\widehat{C}=\dfrac{2}{7}\widehat{B}\)
Ta có: Tam giác ABC vuông tại A
\(\Rightarrow\widehat{B}+\widehat{C}=90^0\)
\(\Rightarrow\widehat{B}+\dfrac{2}{7}\widehat{B}=90^0\)\(\Rightarrow\dfrac{9}{7}\widehat{B}=90^0\Rightarrow\widehat{B}=70^0\)
\(\Rightarrow\widehat{C}=\dfrac{2}{7}\widehat{B}=20^0\)
b) Ta có: AD là phân giác góc A
\(\Rightarrow\widehat{DAC}=\dfrac{1}{2}\widehat{A}=45^0\)
Xét tam giác ADC có:
\(\widehat{ADC}+\widehat{DAC}+\widehat{C}=180^0\)
\(\Rightarrow\widehat{ADC}=180^0-\widehat{DAC}-\widehat{C}=180^0-45^0-20^0=115^0\)
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A; BC a không đổi,
C
^
α
0
0
α
90
0
Tìm góc để diện tích tam giác ABC là lớn nhất. Tính giá trị lớn nhất ấy. A.
α
45
0
;
m...
Đọc tiếp
Cho tam giác ABC vuông tại A; BC = a không đổi, C ^ = α 0 0 < α < 90 0
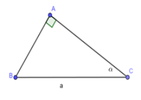
Tìm góc để diện tích tam giác ABC là lớn nhất. Tính giá trị lớn nhất ấy.
A. α = 45 0 ; m a x S A B C = 1 2 a 2 .
B. α = 30 0 ; m a x S A B C = 3 4 a 2 .
C. α = 60 0 ; m a x S A B C = 3 4 a 2 .
D. α = 45 0 ; m a x S A B C = 1 4 a 2 .
S A B C = . AB. AC ≤ 1 2 . A B 2 + A C 2 2 = 1 4 . A B 2 + A C 2
Áp dụng định lý Py-ta-go cho ABC vuông tại A ta có:
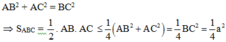
Dấu “=” xảy ra AC = AB => ∆ ABC vuông cân
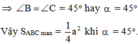
Đáp án cần chọn là: D
Đúng 0
Bình luận (0)
Bài 4 : Cho tam giác ABC có A = 900 . BE là tia phân giác ABC (E thuộcAC).
Trên cạnh BC lấy điểm D sao cho AB = BD.
a) Chứng minh rằng:tam giác ABE = DBE.
b) Chứng minh rằng: DBE là tam giác vuông.
c) Chứng minh rằng: góc ABC = góc DEC .
d) Trên tia đối của tia AB lấy điểm F sao cho AF = DC. Chứng minh rằng: F, E, D thẳng hàng.
a: Xét ΔABE và ΔDBE có
BA=BD
\(\widehat{ABE}=\widehat{DBE}\)
BE chung
Do đó: ΔABE=ΔDBE
Đúng 0
Bình luận (0)
cho tam giác abc có góc A =900 trung tuyển AM=5cm thì cạch huyền BC bằng
Cho tam giác ABC cân tại A, (góc A <900), gọi M là trung điểm của BC.
a) Chứng minh tam giác AMB = tam giác AMC và AM là tia phân giác của góc A.
b) Kẻ BH vuông góc AC (H thuộc AC), CK vuông góc AB (K thuộc AB). Chứng minh tam giác CHB = tam giác BKC.
c) Gọi I là giao điểm của BH và CK. Chứng minh A, I, M thẳng hàng.
a) Xét ΔAMB và ΔAMC có
AM chung
BM=CM(M là trung điểm của BC)
AB=AC(ΔABC cân tại A)
Do đó: ΔABM=ΔACM(c-c-c)
Đúng 1
Bình luận (0)
a) Ta có: ΔAMB=ΔAMC(cmt)
nên \(\widehat{BAM}=\widehat{CAM}\)(hai góc tương ứng)
mà tia AM nằm giữa hai tia AB và AC
nên AM là tia phân giác của \(\widehat{BAC}\)(đpcm)
Đúng 1
Bình luận (0)
b) Xét ΔCHB vuông tại H và ΔBKC vuông tại K có
BC chung
\(\widehat{HCB}=\widehat{KBC}\)(hai góc ở đáy của ΔABC cân tại A)
Do đó: ΔCHB=ΔBKC(cạnh huyền-góc nhọn)
Đúng 1
Bình luận (0)
Xem thêm câu trả lời




