Cho hình thang vuông ABCD , vuông tại A và D ; AB = 1/3 CD. Kéo dài DA và CB cắt nhau tại M.
a. So sánh diện tích các cặp tam giác ABC và ADC; ABM và CAM.
b. Tính diện tích tam giác ABM biết diện tích hình thang ABCD = 64 cm2.
Cho hình thang ABCD vuông góc tại A và D . Hai đường chéo vuông góc với nhau tại O. Biết AB =2√13 , OA =6 . Tính diện tích hình thang ABCD
* Cho hình thang ABCD vuông góc tại A và D. Hai đường chéo vuông góc với nhau tại O. Biết AB=\(2\sqrt{13}\), OA=6, tính diện tích hình thang ABCD
Xét tam giác vuông OAB:
\(OB=\sqrt{AB^2-OA^2}=4\)
Áp dụng hệ thức lượng cho tam giác vuông ABD với đường cao AO:
\(AB^2=OB.BD\Rightarrow BD=\dfrac{AB^2}{OB}=13\)
\(\Rightarrow\left\{{}\begin{matrix}OD=BD-OB=9\\AD=\sqrt{BD^2-AB^2}=\sqrt{29}\end{matrix}\right.\)
\(\widehat{BAO}=\widehat{DCO}\left(slt\right)\Rightarrow\Delta_VAOB\sim\Delta_VCOD\) (g.g)
\(\Rightarrow\dfrac{AB}{DC}=\dfrac{OB}{OD}\Rightarrow DC=\dfrac{AB.OD}{OB}=\dfrac{9\sqrt{13}}{2}\)
\(S_{ABCD}=\dfrac{1}{2}AD.\left(AB+CD\right)=\dfrac{1}{2}.\sqrt{29}.\left(2\sqrt{13}+\dfrac{9\sqrt{13}}{2}\right)=...\)
Cho hình thang vuông ABCD vuông góc tại A và D ,AB=1 PHẦN 3 CD . Kéo dài DA và CB cắt nhau tại M . Diện tích hình thang ABCD là 64 cm vuông . tính diện tích tam giác MBA
Cho hình thang vuông ABCD vuông tại A và D, cho AB= 1/3 CD. Kéo dài BC và AD cắt nhau tại M. Diện tích hình thang ABCD= 64 cm2. Tính diện tích tam giác MAB
Xét ΔMCD có AB//CD
nên ΔMAB~ΔMDC
=>\(\dfrac{S_{MAB}}{S_{MDC}}=\left(\dfrac{AB}{CD}\right)^2=\dfrac{1}{9}\)
=>\(S_{MAB}=\dfrac{1}{9}\cdot S_{MDC}\)
Ta có: \(S_{MAB}+S_{ABCD}=S_{MDC}\)
=>\(S_{ABCD}=S_{MDC}-\dfrac{1}{9}\cdot S_{MDC}=\dfrac{8}{9}\cdot S_{MDC}\)
=>\(S_{MDC}=64:\dfrac{8}{9}=72\left(cm^2\right)\)
=>\(S_{MAB}=\dfrac{1}{9}\cdot72=8\left(cm^2\right)\)
Cho hình thang ABCD vuông góc tại A và D. Hai đường chéo vuông góc với nhau tại O. Biết AB= 2 căn 13, OA=6. Tính diện tích hình thang ABCD.
Cho hình thang vuông ABCD vuông góc tại A và D; AB = 1 3 CD. Kéo dài DA và CB cắt nhau tại M.
c) Diện tích hình thang ABCD bằng 64 cm2.Tính diện tích tam giác MBA .
cho hình thang vuông tại A và D, 2 đường chéo AC và DB cắt nhau và vuông góc tại O, biết AB=2√13, OA=6. Tính diện tích hình thang ABCD
Cho hình thang ABCD vuông tại A và D; C ^ = 50 0 . Biết AB = 2; AD = 1,2. Tính diện tích hình thang ABCD
A. S A B C D = 2 (đvdt)
B. S A B C D = 3 (đvdt)
C. S A B C D = 4 (đvdt)
D. S A B C D = 5 2 (đvdt)
Cho hình thang vuông ABCD ( ∠ A = ∠ D = 90 0 ) có hai đường chéo AC và BD vuông góc với nhau tại H. Biết HD = 18cm, HB = 8cm, tính diện tích hình thang ABCD
A. 504 c m 2
B. 505 c m 2
C. 506 c m 2
D. 506 c m 2
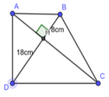
Xét ∆ ADB vuông tại A có: AH là đường cao ứng với cạnh huyền BD
⇒ A H 2 = HB. HD = 8.18 HA = 12 (cm) (hệ thức lượng trong tam giác vuông)
Xét ∆ ADC vuông tại D có: DH là đường cao ứng với cạnh huyền AC
⇒ H D 2 = H A . H C ⇒ 18 2 = 12 H C => HC = 27 (cm) (hệ thức lượng trong tam giác vuông)
Ta có: AC = AH + HC = 12 + 27 = 39 cm
BD = BH + HD = 8 + 18 = 26cm
S A B C D = A C . B D 2 = 26.39 2 = 507 c m 2
Đáp án cần chọn là: D
Cho hình thang vuông ABCD có A ^ = D ^ = 90 0 , AB = AD = 2 cm, DC = 4 cm và BH vuông góc với CD tại H.
a) Chứng minh ∆ABD = ∆HDB.
b) Chứng minh tam giác BHC vuông cân tại H.
c) Tính diện tích hình thang ABCD