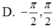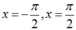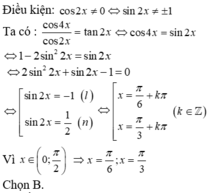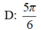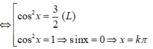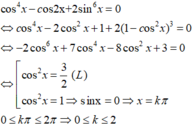1) tìm nghiệm của phương trình: \(\frac{cos4x}{cos2x}=tan2x\) trong khoảng \(\left(0;\frac{\pi}{2}\right)\)
2) tìm tất cả các nghiệm của phương trình: sin8x+cos4x=1+2sin2x.cos6x thuộc \(\left(-\pi;\pi\right)\)
3) tìm tất cả các nghiệm của phương trình: \(\frac{\sqrt{3}sin3x-2sinx.sin2x-cosx}{sinx}=0\) thuộc \(\left[-\frac{\pi}{2};\frac{\pi}{2}\right]\)
4) tìm tất cả các nghiệm của phương trình: sinx+ sin2x+ sin3x=0 thuộc \(\left(0;\pi\right)\)