Cho hàm số f(x) liên tục trên \([-\Pi;\Pi]\)
Chứng minh: \(\int\limits^{\Pi}_0x.f\left(sinx\right)dx=\dfrac{\Pi}{2}\int\limits^{\Pi}_0f\left(sinx\right)dx\)
NA
Những câu hỏi liên quan
NH
13 tháng 5 2022 lúc 0:49
Cho hàm số y=f(x) liên tục trên [0;+\(\infty\)] và \(\int_0^{x^2}f\left(t\right)dt=x.sin\pi x\). Tính f(4)
đặt :
\(F\left(x\right)=\int_0^{x^2}f\left(t\right)dt=xsin\left(\pi x\right)\Leftrightarrow F\left(x^2\right)-F\left(0\right)=xsin\)
\(\left(\pi x\right)\Leftrightarrow F\left(x^2\right)=F\left(0\right)+xsin\left(\pi x\right)\)
lấy đạo hàm \(2\) vế , ta có :
\(\left(F\left(0\right)\right)'=sin\left(\pi x\right)+\pi xcos\left(\pi x\right)+\left(F\left(0\right)\right)'\)
\(\Leftrightarrow2xf\left(x^2\right)=sin\left(\pi x\right)+\pi xcos\left(\pi x\right)\)
thay \(x=2\) , ta có :
\(2.2.f\left(4\right)=sin\left(2\pi\right)+2\pi cos\left(2\pi\right)\Leftrightarrow4f\left(4\right)=2\pi\Leftrightarrow f\left(4\right)=\dfrac{\pi}{2}\)
Đúng 1
Bình luận (0)
Cho hàm số yfleft(xright) có đạo hàm và liên tục trên left[0;dfrac{pi}{2}right]thoả mãn fleft(xright)fleft(xright)-2cosx. Biết fleft(dfrac{pi}{2}right)1, tính giá trị fleft(dfrac{pi}{3}right)A. dfrac{sqrt{3}+1}{2} B. dfrac{sqrt{3}-1}{2} C. dfrac{1-sqrt{3}}{2} D. 0
Đọc tiếp
Cho hàm số \(y=f\left(x\right)\) có đạo hàm và liên tục trên \(\left[0;\dfrac{\pi}{2}\right]\)thoả mãn \(f\left(x\right)=f'\left(x\right)-2cosx\). Biết \(f\left(\dfrac{\pi}{2}\right)=1\), tính giá trị \(f\left(\dfrac{\pi}{3}\right)\)
A. \(\dfrac{\sqrt{3}+1}{2}\) B. \(\dfrac{\sqrt{3}-1}{2}\) C. \(\dfrac{1-\sqrt{3}}{2}\) D. 0
Cho hàm số y=f(x)y=f(x) có đạo hàm và liên tục trên [0;π2][0;π2]thoả mãn f(x)=f′(x)−2cosxf(x)=f′(x)−2cosx. Biết f(π2)=1f(π2)=1, tính giá trị f(π3)f(π3)
A. √3+1/2 B. √3−1/2 C. 1−√3/2 D. 0
Đúng 1
Bình luận (0)
\(f'\left(x\right)-f\left(x\right)=2cosx\)
\(\Leftrightarrow e^{-x}.f'\left(x\right)-e^{-x}.f\left(x\right)=2e^{-x}cosx\)
\(\Rightarrow\left[e^{-x}.f\left(x\right)\right]'=2e^{-x}.cosx\)
Lấy nguyên hàm 2 vế:
\(\Rightarrow e^{-x}.f\left(x\right)=\int2e^{-x}cosxdx=e^{-x}\left(sinx-cosx\right)+C\)
Thay \(x=\dfrac{\pi}{2}\Rightarrow e^{-\dfrac{\pi}{2}}.1=e^{-\dfrac{\pi}{2}}+C\Rightarrow C=0\)
\(\Rightarrow f\left(x\right)=sinx-cosx\)
\(\Rightarrow f\left(\dfrac{\pi}{3}\right)=\dfrac{\sqrt{3}-1}{2}\)
Đúng 1
Bình luận (0)
Cho hàm số f(x) liên tục trên R Biết cận 0->pi/2 sin2x f(cos^2(x)) dx =1 Khi đó cân 0->1[2f(1-x) -3x^2+5]dx=?
Đề là cho \(\int\limits^{\dfrac{\pi}{2}}_0sin2x.f\left(cos^2x\right)dx=1\)
Tính \(\int\limits^1_0\left[2f\left(1-x\right)-3x^2+5\right]dx\)
Đúng ko nhỉ?
Xét \(\int\limits^{\dfrac{\pi}{2}}_0sin2x.f\left(cos^2x\right)dx\)
Đặt \(cos^2x=1-u\Rightarrow-2sinx.cosxdx=-du\) \(\Rightarrow sin2xdx=du\)
\(\left\{{}\begin{matrix}x=0\Rightarrow u=0\\x=\dfrac{\pi}{2}\Rightarrow u=1\end{matrix}\right.\) \(\Rightarrow I=\int\limits^1_0f\left(1-u\right)du=\int\limits^1_0f\left(1-x\right)dx\)
\(\Rightarrow\int\limits^1_0f\left(1-x\right)dx=1\)
\(\Rightarrow\int\limits^1_0\left[2f\left(1-x\right)-3x^2+5\right]dx=2\int\limits^1_0f\left(1-x\right)dx-\int\limits^1_0\left(3x^2-5\right)dx\)
\(=2.1-\left(-4\right)=6\)
Đúng 1
Bình luận (2)
Cho hàm số y f(x) liên tục trên [a;b]. Giả sử hàm số u u(x) có đạo hàm liên tục trên [a;b] và
u
(
x
)
∈
[
α
;
β
]
∀
x
∈
[
a
;
b
]
hơn nữa f(u) liên...
Đọc tiếp
Cho hàm số y = f(x) liên tục trên [a;b]. Giả sử hàm số u = u(x) có đạo hàm liên tục trên [a;b] và u ( x ) ∈ [ α ; β ] ∀ x ∈ [ a ; b ] hơn nữa f(u) liên tục trên đoạn [a;b]. Mệnh đề nào sau đây là đúng?
A. ∫ a b f ( u ( x ) ) u ' d x = ∫ u ( a ) u ( b ) f ( u ) d u
B. ∫ a b f ( u ( x ) ) u ' d x = ∫ a b f ( u ) d u
C. ∫ u ( a ) u ( b ) f ( u ( x ) ) u ' d x = ∫ a b f ( u ) d u
D. ∫ a b f ( u ( x ) ) u ' d x = ∫ a b f ( x ) d x
Phương pháp: Sử dụng phương pháp đổi biến, đặt t = u(x)
Cách giải:
Đặt
Đổi cận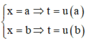 
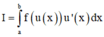
Đúng 0
Bình luận (0)
Cho hàm số y f(x) liên tục trên [a;b] Giả sử hàm số u u(x) có đạo hàm liên tục trên [a;b] và
u
(
x
)
∈
[
a
;
b
]
hơn nữa u(x) liên tục trên đoạn [a;b]Mệnh đề nào sau đây là đúng?
Đọc tiếp
Cho hàm số y = f(x) liên tục trên [a;b] Giả sử hàm số u = u(x) có đạo hàm liên tục trên [a;b] và u ( x ) ∈ [ a ; b ] hơn nữa u(x) liên tục trên đoạn [a;b]Mệnh đề nào sau đây là đúng?
Cho hàm số yf(x) liên tục trên khoảng (a;b). Điều kiện cần và đủ để hàm số liên tục trên đoạn [a;b] là? A.
lim
x
→
a
+
f
x
f
a
và
lim
x
→
b
−...
Đọc tiếp
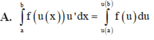
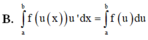
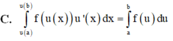
Cho hàm số y=f(x) liên tục trên khoảng (a;b). Điều kiện cần và đủ để hàm số liên tục trên đoạn [a;b] là?
A. lim x → a + f x = f a và lim x → b − f x = f b
B. lim x → a − f x = f a và lim x → b + f x = f b
C. lim x → a + f x = f a và lim x → b + f x = f b
D. lim x → a − f x = f a và lim x → b − f x = f b
Cho hàm số f(x) liên tục trên có f(0) 0 và đồ thị hàm số y f’(x) như hình vẽ bên. Hàm số đồng biến trên khoảng A.
2
;
+
∞
B.
-
∞
;
2
C. (0;2) D. (1;3)
Đọc tiếp
Cho hàm số f(x) liên tục trên có f(0) = 0 và đồ thị hàm số y = f’(x) như hình vẽ bên. Hàm số đồng biến trên khoảng
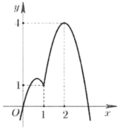
A. 2 ; + ∞
B. - ∞ ; 2
C. (0;2)
D. (1;3)
Cho hàm số
y
f
(
x
)
liên tục trên R và có hàm số
y
f
(
x
)
thoả mãn. Số cực trị của hàm số
y
f
(
x
)
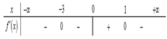
là A. 3 B. 1 C. 0 D. 2
Đọc tiếp
Cho hàm số y = f ( x ) liên tục trên R và có hàm số y = f ' ( x ) thoả mãn. Số cực trị của hàm số y = f ( x ) là
A. 3
B. 1
C. 0
D. 2
Cho hàm số yf(x) có đạo hàm liên tục trên R. Bảng biến thiên của hàm số yf(x) được cho như hình vẽ bên. Hàm số
y
f
(
1
-
x
2
)
+
x
nghịch biến trên khoảng A. (-4;-2) B. (2;4) C. (0;2) D. (-2;0)
Đọc tiếp
Cho hàm số y=f(x) có đạo hàm liên tục trên R. Bảng biến thiên của hàm số y=f'(x) được cho như hình vẽ bên. Hàm số y = f ( 1 - x 2 ) + x nghịch biến trên khoảng
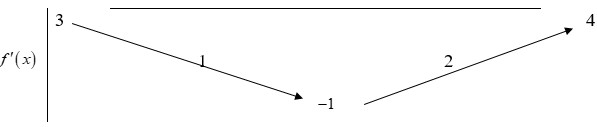
A. (-4;-2)
B. (2;4)
C. (0;2)
D. (-2;0)
