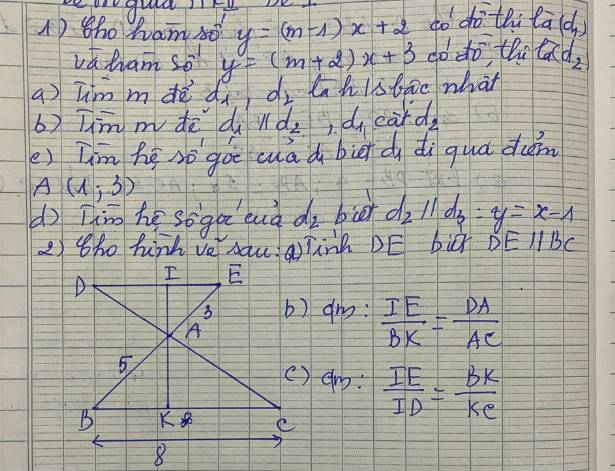Phân thức đại số
Bài 1:
a: Thay x=-1 và y=-1 vào (d1), ta được:
\(-\left(m+1\right)+2=-1\)
=>-m-1+2=-1
=>-m+1=-1
=>-m=-2
=>m=2
b: Tọa độ điểm B là:
\(\left\{{}\begin{matrix}-2x+1=x+2\\y=x+2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}-3x=1\\y=x+2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-\dfrac{1}{3}\\y=-\dfrac{1}{3}+2=\dfrac{5}{3}\end{matrix}\right.\)
vậy: \(B\left(-\dfrac{1}{3};\dfrac{5}{3}\right)\)
c: Thay x=-1/3 và y=5/3 vào (d1), ta được:
\(-\dfrac{1}{3}\left(m+1\right)+2=\dfrac{5}{3}\)
=>\(-\dfrac{1}{3}\left(m+1\right)=-\dfrac{1}{3}\)
=>m+1=1
=>m=0
d: Vì \(\left\{{}\begin{matrix}-2=-2\\1\ne2\end{matrix}\right.\)
nên (d2)//(d4)
Vì \(1\ne-2\)
nên (d3) cắt (d4)
Bài 2:
a: Xét ΔAEI có
K là trung điểm của AI
KM//EI
Do đó: M là trung điểm của AE
=>AM=ME
Xét hình thang BMKH có
I là trung điểm của KH
IE//MK//BH
Do đó:E là trung điểm của MB
=>ME=EB
=>AM=ME=EB
b: Xét ΔABC có MN//BC
nên \(\dfrac{MN}{BC}=\dfrac{AM}{AB}\)
=>\(\dfrac{MN}{30}=\dfrac{1}{3}\)
=>MN=30/3=10(cm)
Xét ΔABC có EF//BC
nên \(\dfrac{EF}{BC}=\dfrac{AE}{AB}\)
=>\(\dfrac{EF}{30}=\dfrac{2}{3}\)
=>\(EF=30\cdot\dfrac{2}{3}=20\left(cm\right)\)
c: Xét ΔABC có MN//BC
nên ΔAMN~ΔABC theo hệ số tỉ lệ là \(k=\dfrac{AM}{AB}=\dfrac{1}{3}\)
=>\(\dfrac{S_{AMN}}{S_{ABC}}=\left(\dfrac{1}{3}\right)^2=\dfrac{1}{9}\)
=>\(S_{AMN}=\dfrac{1}{9}\cdot S_{ABC}\)
Ta có: \(S_{AMN}+S_{BMNC}=S_{ABC}\)
=>\(S_{BMNC}=\dfrac{8}{9}\cdot S_{ABC}\)
=>\(S_{ABC}=200:\dfrac{8}{9}=225\left(cm^2\right)\)
d: Xét ΔAMN và ΔABC có
\(\widehat{AMN}=\widehat{ABC}\)(hai góc đồng vị, MN//BC)
\(\widehat{MAN}\) chung
Do đó: ΔAMN~ΔABC
=>\(k=\dfrac{AM}{AB}=\dfrac{1}{3}\)
Xét ΔAEF và ΔABC có
\(\widehat{AEF}=\widehat{ABC}\)(hai góc đồng vị, EF//BC)
\(\widehat{FAE}\) chung
Do đó: ΔAEF~ΔABC
=>\(k=\dfrac{AE}{AB}=\dfrac{2}{3}\)
Đúng 1
Bình luận (0)
Bài 1:
a: 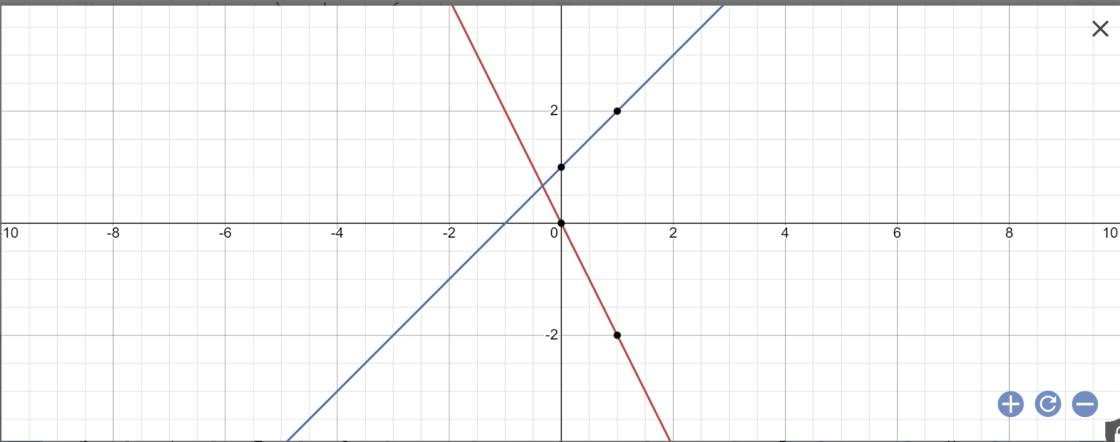
b: Phương trình hoành độ giao điểm là:
-2x=x+1
=>-2x-x=1
=>-3x=1
=>x\(=-\dfrac{1}{3}\)
Thay \(x=-\dfrac{1}{3}\) vào y=-2x, ta được:
\(y=-2\cdot\dfrac{-1}{3}=\dfrac{2}{3}\)
vậy: \(D\left(-\dfrac{1}{3};\dfrac{2}{3}\right)\)
Bài 2:
Thay x=1 và y=5 vào y=(m-1)x+3, ta được:
1(m-1)+3=5
=>m+2=5
=>m=3
=>Hệ số góc của hàm số y=(m-1)x+3 là m-1=3-1=2
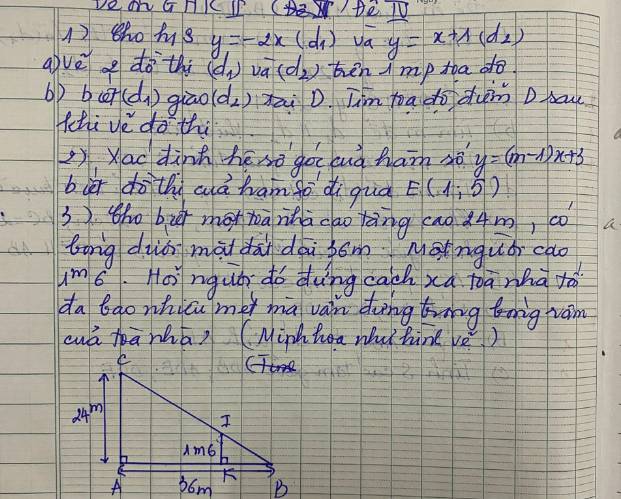
3: Xét ΔBAC có KI//AC
nên \(\dfrac{KI}{AC}=\dfrac{BK}{BA}\)
=>\(\dfrac{BK}{36}=\dfrac{1.6}{24}=\dfrac{1}{15}\)
=>\(BK=\dfrac{36}{15}=2,4\left(m\right)\)
Ta có: BK+KA=BA
=>KA=36-2,4=33,6(m)
=>Người đó cần đứng cách tối đa là 33,6m để vẫn đứng trong bóng râm của tòa nhà
Đúng 1
Bình luận (0)
a: Thay x=1 và y=2 vào y=ax+1, ta được:
\(a\cdot1+1=2\)
=>a+1=2
=>a=1
b: Thay x=-1/3 và y=0 vào y=ax+1, ta được:
\(-\dfrac{1}{3}a+1=0\)
=>\(-\dfrac{1}{3}a=-1\)
=>a=3
c: Thay x=-4/3 vào \(y=\dfrac{1}{2}x-1\), ta được:
\(y=\dfrac{1}{2}\cdot\dfrac{-4}{3}-1=-\dfrac{2}{3}-1=-\dfrac{5}{3}\)
Thay \(x=-\dfrac{4}{3};y=-\dfrac{5}{3}\) vào y=ax+1, ta được:
\(a\cdot\dfrac{-4}{3}+1=-\dfrac{5}{3}\)
=>\(a\cdot\dfrac{-4}{3}=-\dfrac{8}{3}\)
=>a=2
d: Thay y=2 vào (d2), ta được:
\(\dfrac{1}{2}x-1=2\)
=>\(\dfrac{1}{2}x=3\)
=>x=6
Thay x=6 và y=2 vào (d1), ta được:
\(a\cdot6+1=2\)
=>6a=1
=>\(a=\dfrac{1}{6}\)
Đúng 1
Bình luận (0)
Bài 3:
a: Gọi hàm số cần tìm có dạng là y=ax+b(a<>0)
Vì hệ số góc là -1 nên a=-1
=>y=-x+b
Thay x=0 và y=1 vào y=-x+b, ta được:
b-0=1
=>b=1
=>y=-x+1
b: Gọi hàm số cần tìm có dạng là y=ax+b(a<>0)
Hệ số góc của y=2x-1 nên a=2
=>y=2x+b
Thay x=1 và y=3 vào y=2x+b, ta được:
\(2\cdot1+b=3\)
=>b+2=3
=>b=1
=>y=2x+1
c: Đặt (d1): y=-x+1; (d2): y=2x+1
Bảng giá trị:
| x | 0 | 1 |
| y=-x+1 | 1 | 0 |
| y=2x+1 | 1 | 3 |
Vẽ đồ thị:
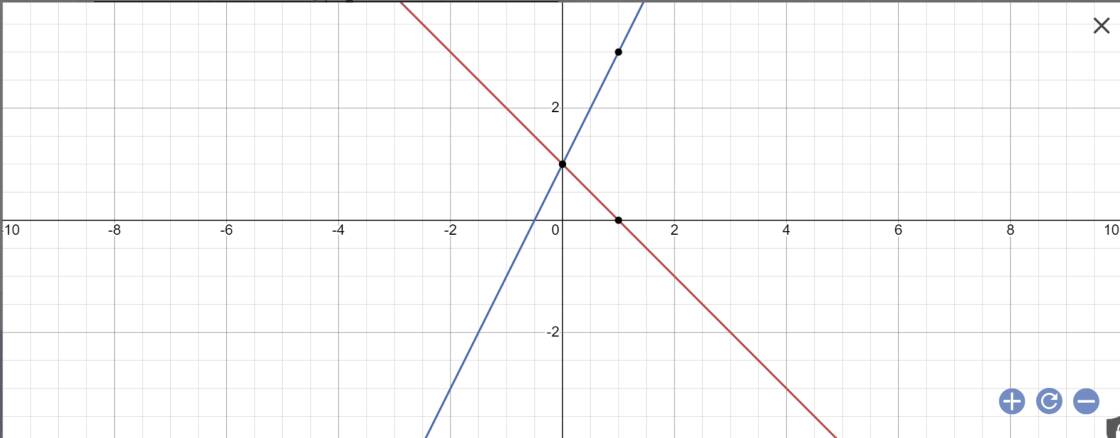
d: Tọa độ A là:
\(\left\{{}\begin{matrix}y=0\\-x+1=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=0\\-x=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=0\\x=1\end{matrix}\right.\)
Vậy: A(1;0)
Tọa độ B là:
\(\left\{{}\begin{matrix}x=0\\y=-x+1=-0+1=1\end{matrix}\right.\)
Vậy: B(0;1)
Vì Ox\(\perp\)Oy
nên OA\(\perp\)OB
=>ΔOAB vuông tại O
O(0;0); A(1;0); B(0;1)
\(OA=\sqrt{\left(1-0\right)^2+\left(0-0\right)^2}=1\)
\(OB=\sqrt{\left(0-0\right)^2+\left(1-0\right)^2}=1\)
\(AB=\sqrt{\left(0-1\right)^2+\left(1-0\right)^2}=\sqrt{1+1}=\sqrt{2}\)
Chu vi tam giác OAB là:
\(1+1+\sqrt{2}=2+\sqrt{2}\)
Ta có: ΔOAB vuông tại O
=>\(S_{OAB}=\dfrac{1}{2}\cdot OA\cdot OB=\dfrac{1}{2}\)
Bài 2:
y=(m-2)x+m-3
=mx-2x+m-3
=m(x+1)-2x-3
Tọa độ điểm cố định mà đường thẳng y=(m-2)x+m-3 luôn đi qua là:
\(\left\{{}\begin{matrix}x+1=0\\y=-2x-3\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=-1\\y=-2\cdot\left(-1\right)-3=2-3=-1\end{matrix}\right.\)
=>A(-1;-1) là điểm cố định mà đường thẳng y=(m-2)x+m-3 luôn đi qua
Đúng 1
Bình luận (0)
cho tôi xin hình với ạ
Câu 2:
a: Xét ΔABC có AD là phân giác
nên \(\dfrac{DB}{AB}=\dfrac{DC}{AC}\)
=>\(\dfrac{DB}{15}=\dfrac{DC}{20}\)
=>\(\dfrac{DB}{3}=\dfrac{DC}{4}\)
mà DB+DC=BC=25cm
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{DB}{3}=\dfrac{DC}{4}=\dfrac{DB+DC}{3+4}=\dfrac{25}{7}\)
=>\(DB=\dfrac{25}{7}\cdot3=\dfrac{75}{7}\left(cm\right);DC=\dfrac{25}{7}\cdot4=\dfrac{100}{7}\left(cm\right)\)
Xét ΔCAB có ED//AB
nên \(\dfrac{ED}{AB}=\dfrac{CD}{CB}\)
=>\(\dfrac{ED}{15}=\dfrac{4}{7}\)
=>\(ED=\dfrac{4}{7}\cdot15=\dfrac{60}{7}\left(cm\right)\)
b: Xét ΔABC có \(AB^2+AC^2=BC^2\)
nên ΔABC vuông tại A
=>\(S_{ABC}=\dfrac{1}{2}\cdot AB\cdot AC=\dfrac{1}{2}\cdot15\cdot20=10\cdot15=150\left(cm^2\right)\)
Xét ΔABC có AH là đường cao
nên \(S_{ABC}=\dfrac{1}{2}\cdot AH\cdot BC\)
=>\(AH\cdot25=2\cdot150=300\)
=>\(AH=\dfrac{300}{25}=12\left(cm\right)\)
c: Ta có: \(\dfrac{BD}{BC}=\dfrac{75}{7}:25=\dfrac{3}{7}\)
=>\(S_{ABD}=\dfrac{3}{7}\cdot S_{ABC}=\dfrac{3}{7}\cdot150=\dfrac{450}{7}\left(cm^2\right)\)
=>\(S_{ACD}=S_{ABC}-S_{ABD}=150-\dfrac{450}{7}=\dfrac{600}{7}\left(cm^2\right)\)
Xét ΔCAB có ED//AB
nên \(\dfrac{CE}{CA}=\dfrac{ED}{AB}=\dfrac{CD}{CB}=\dfrac{4}{7}\)
=>\(S_{CED}=\dfrac{4}{7}\cdot S_{CAD}=\dfrac{4}{7}\cdot\dfrac{600}{7}=\dfrac{2400}{49}\left(cm^2\right)\)
Ta có: \(S_{CDE}+S_{AED}=S_{CAD}\)
=>\(S_{AED}=\dfrac{3}{7}\cdot S_{CAD}=\dfrac{3}{7}\cdot\dfrac{600}{7}=\dfrac{1800}{49}\left(cm^2\right)\)
Bài 1:
a: 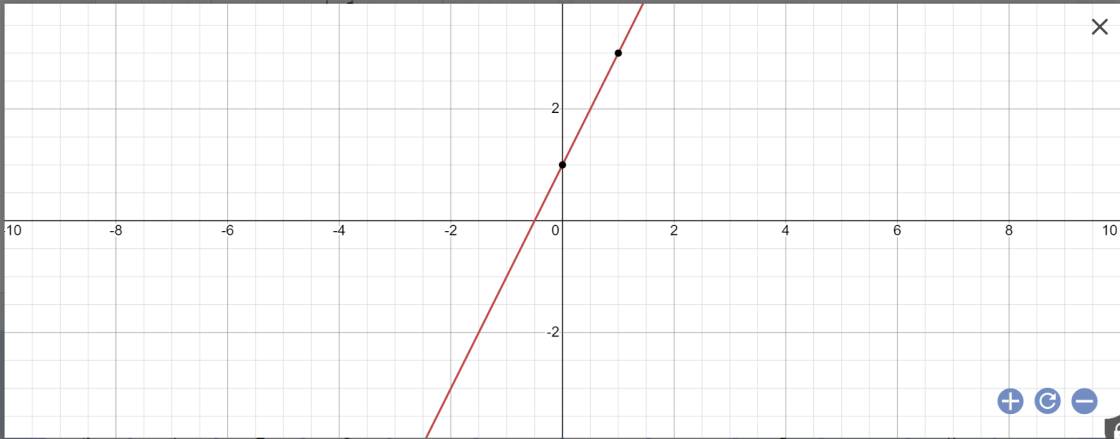
b: Để (d1)//(d2) thì \(\left\{{}\begin{matrix}m-2=2\\m\ne1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m=4\\m\ne1\end{matrix}\right.\)
=>m=4
c: Thay x=2 và y=-3 vào (d1), ta được:
\(2\left(m-2\right)+m=-3\)
=>2m-4+m=-3
=>3m=-3+4=1
=>\(m=\dfrac{1}{3}\)
d: Để (d1) cắt (d2) tại một điểm trên trục tung thì
\(\left\{{}\begin{matrix}m-2\ne2\\m=1\end{matrix}\right.\)
=>m=1
Đúng 4
Bình luận (0)
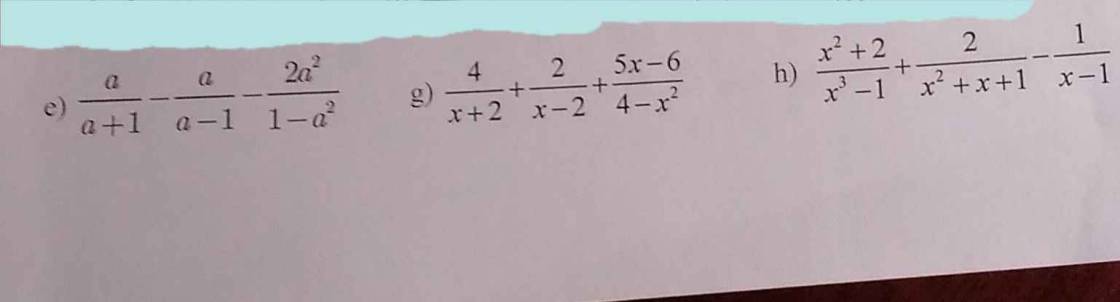 chi tiết
chi tiết
e: ĐKXĐ: \(a\notin\left\{-1;1\right\}\)
\(\dfrac{a}{a+1}-\dfrac{a}{a-1}-\dfrac{2a^2}{1-a^2}\)
\(=\dfrac{a}{a+1}-\dfrac{a}{a-1}+\dfrac{2a^2}{\left(a-1\right)\left(a+1\right)}\)
\(=\dfrac{a\left(a-1\right)-a\left(a+1\right)+2a^2}{\left(a+1\right)\left(a-1\right)}\)
\(=\dfrac{a^2-a-a^2-a+2a^2}{\left(a+1\right)\left(a-1\right)}=-\dfrac{2a}{a^2-1}\)
g: ĐKXĐ: \(x\notin\left\{2;-2\right\}\)
\(\dfrac{4}{x+2}+\dfrac{2}{x-2}+\dfrac{5x-6}{4-x^2}\)
\(=\dfrac{4}{x+2}+\dfrac{2}{x-2}-\dfrac{5x-6}{\left(x-2\right)\left(x+2\right)}\)
\(=\dfrac{4\left(x-2\right)+2\left(x+2\right)-5x+6}{\left(x-2\right)\left(x+2\right)}\)
\(=\dfrac{4x-8+2x+4-5x+6}{\left(x-2\right)\left(x+2\right)}=\dfrac{x+2}{\left(x-2\right)\left(x+2\right)}=\dfrac{1}{x-2}\)
h: ĐKXĐ: x<>1
\(\dfrac{x^2+2}{x^3-1}+\dfrac{2}{x^2+x+1}-\dfrac{1}{x-1}\)
\(=\dfrac{x^2+2}{\left(x-1\right)\left(x^2+x+1\right)}+\dfrac{2}{x^2+x+1}-\dfrac{1}{x-1}\)
\(=\dfrac{x^2+2+2\left(x-1\right)-x^2-x-1}{\left(x-1\right)\left(x^2+x+1\right)}\)
\(=\dfrac{-x+1+2x-2}{\left(x-1\right)\left(x^2+x+1\right)}=\dfrac{1}{x^2+x+1}\)
Đúng 1
Bình luận (0)
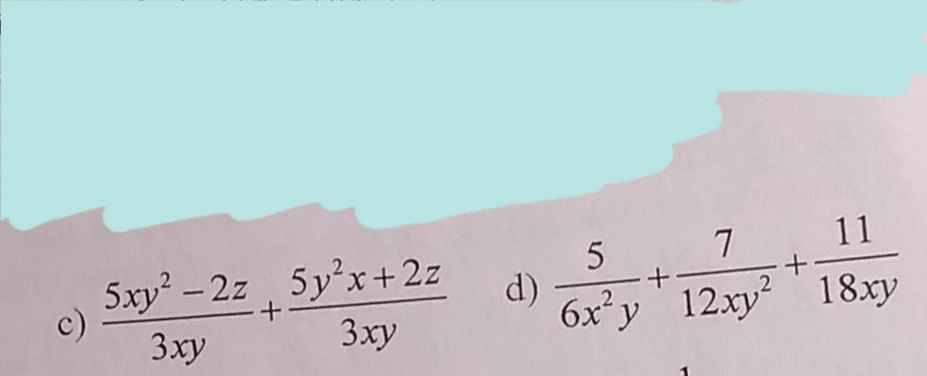 cchIchI titietiêtiêttiết
cchIchI titietiêtiêttiết
\(\dfrac{5xy^2-2z}{3xy}+\dfrac{5y^2x+2z}{3xy}=\dfrac{5xy^2-2z+5y^2x+2z}{3xy}\)
\(=\dfrac{5x^2y+5y^2x}{3xy}=\dfrac{5xy\left(x+y\right)}{3xy}=\dfrac{5\left(x+y\right)}{3}\)
d.
\(\dfrac{5}{6x^2y}+\dfrac{7}{12xy^2}+\dfrac{11}{18xy}=\dfrac{30y}{36x^2y^2}+\dfrac{21x}{36x^2y^2}+\dfrac{22xy}{36x^2y^2}\)
\(=\dfrac{22xy+21x+30y}{36x^2y^2}\)
Đúng 1
Bình luận (0)
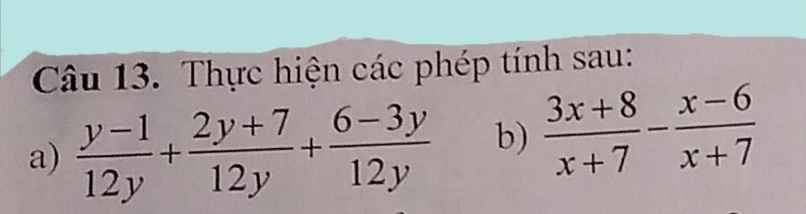 chi tiêtiêttiết nhất
chi tiêtiêttiết nhất
\(\dfrac{y-1}{12y}+\dfrac{2y+7}{12y}+\dfrac{6-3y}{12y}=\dfrac{y-1+2y+7+6-3y}{12y}=\dfrac{12}{12y}=\dfrac{1}{y}\)
\(\dfrac{3x+8}{x+7}-\dfrac{x-6}{x+7}=\dfrac{3x+8-\left(x-6\right)}{x+7}=\dfrac{3x+8-x+6}{x+7}=\dfrac{2x+14}{x+7}=\dfrac{2\left(x+7\right)}{x+7}=2\)
Đúng 1
Bình luận (0)
Bài 1:
a: Để (d1) là hàm số bậc nhất thì \(m-1\ne0\)
=>\(m\ne1\)
Để (d2) là hàm số bậc hai thì \(m+2\ne0\)
=>\(m\ne-2\)
b: Để (d1)//(d2) thì \(\left\{{}\begin{matrix}m-1=m+2\\2\ne3\left(đúng\right)\end{matrix}\right.\)
=>m-1=m+2
=>-1=2(sai)
=>\(m\in\varnothing\)
Để (d1) cắt (d2) thì \(m-1\ne m+2\)
=>\(-3\ne0\)(đúng)
=>\(m\in R\)
c: Thay x=1 và y=3 vào (d1), ta được:
\(1\left(m-1\right)+2=3\)
=>m-1+2=3
=>m+1=3
=>m=2
Hệ số góc của (d1) là 2-1=1
d: Để (d2)//(d3) thì \(\left\{{}\begin{matrix}m+2=1\\3\ne-1\left(đúng\right)\end{matrix}\right.\)
=>m+2=1
=>m=-1
Hệ số góc của (d2) là m+2=-1+2=1
Bài 2:
a: Xét ΔAED và ΔABC có
\(\widehat{AED}=\widehat{ABC}\)(hai góc so le trong, ED//BC)
\(\widehat{EAD}=\widehat{BAC}\)(hai góc đối đỉnh)
Do đó; ΔAED~ΔABC
=>\(\dfrac{AE}{AB}=\dfrac{AD}{AC}=\dfrac{ED}{BC}\)
=>\(\dfrac{3}{5}=\dfrac{DE}{8}\)
=>\(DE=3\cdot\dfrac{8}{5}=3\cdot1,6=4,8\)
b: Xét ΔAEI và ΔABK có
\(\widehat{AEI}=\widehat{ABK}\)(hai góc so le trong, EI//BK)
\(\widehat{EAI}=\widehat{BAK}\)(hai góc đối đỉnh)
Do đó: ΔAEI đồng dạng với ΔABK
=>\(\dfrac{EI}{BK}=\dfrac{AE}{AB}\)
mà \(\dfrac{AE}{AB}=\dfrac{AD}{AC}\)
nên \(\dfrac{EI}{BK}=\dfrac{AD}{AC}\)
c: Xét ΔAID và ΔAKC có
\(\widehat{AID}=\widehat{AKC}\)(hai góc so le trong, ID//KC)
\(\widehat{IAD}=\widehat{KAC}\)(hai góc đối đỉnh)
Do đó: ΔAID~ΔAKC
=>\(\dfrac{ID}{KC}=\dfrac{AD}{AC}\)
=>\(\dfrac{ID}{KC}=\dfrac{EI}{BK}\)
=>\(\dfrac{IE}{ID}=\dfrac{BK}{KC}\)
Đúng 1
Bình luận (0)