Bài 1:
a: Để (d1) là hàm số bậc nhất thì \(m-1\ne0\)
=>\(m\ne1\)
Để (d2) là hàm số bậc hai thì \(m+2\ne0\)
=>\(m\ne-2\)
b: Để (d1)//(d2) thì \(\left\{{}\begin{matrix}m-1=m+2\\2\ne3\left(đúng\right)\end{matrix}\right.\)
=>m-1=m+2
=>-1=2(sai)
=>\(m\in\varnothing\)
Để (d1) cắt (d2) thì \(m-1\ne m+2\)
=>\(-3\ne0\)(đúng)
=>\(m\in R\)
c: Thay x=1 và y=3 vào (d1), ta được:
\(1\left(m-1\right)+2=3\)
=>m-1+2=3
=>m+1=3
=>m=2
Hệ số góc của (d1) là 2-1=1
d: Để (d2)//(d3) thì \(\left\{{}\begin{matrix}m+2=1\\3\ne-1\left(đúng\right)\end{matrix}\right.\)
=>m+2=1
=>m=-1
Hệ số góc của (d2) là m+2=-1+2=1
Bài 2:
a: Xét ΔAED và ΔABC có
\(\widehat{AED}=\widehat{ABC}\)(hai góc so le trong, ED//BC)
\(\widehat{EAD}=\widehat{BAC}\)(hai góc đối đỉnh)
Do đó; ΔAED~ΔABC
=>\(\dfrac{AE}{AB}=\dfrac{AD}{AC}=\dfrac{ED}{BC}\)
=>\(\dfrac{3}{5}=\dfrac{DE}{8}\)
=>\(DE=3\cdot\dfrac{8}{5}=3\cdot1,6=4,8\)
b: Xét ΔAEI và ΔABK có
\(\widehat{AEI}=\widehat{ABK}\)(hai góc so le trong, EI//BK)
\(\widehat{EAI}=\widehat{BAK}\)(hai góc đối đỉnh)
Do đó: ΔAEI đồng dạng với ΔABK
=>\(\dfrac{EI}{BK}=\dfrac{AE}{AB}\)
mà \(\dfrac{AE}{AB}=\dfrac{AD}{AC}\)
nên \(\dfrac{EI}{BK}=\dfrac{AD}{AC}\)
c: Xét ΔAID và ΔAKC có
\(\widehat{AID}=\widehat{AKC}\)(hai góc so le trong, ID//KC)
\(\widehat{IAD}=\widehat{KAC}\)(hai góc đối đỉnh)
Do đó: ΔAID~ΔAKC
=>\(\dfrac{ID}{KC}=\dfrac{AD}{AC}\)
=>\(\dfrac{ID}{KC}=\dfrac{EI}{BK}\)
=>\(\dfrac{IE}{ID}=\dfrac{BK}{KC}\)
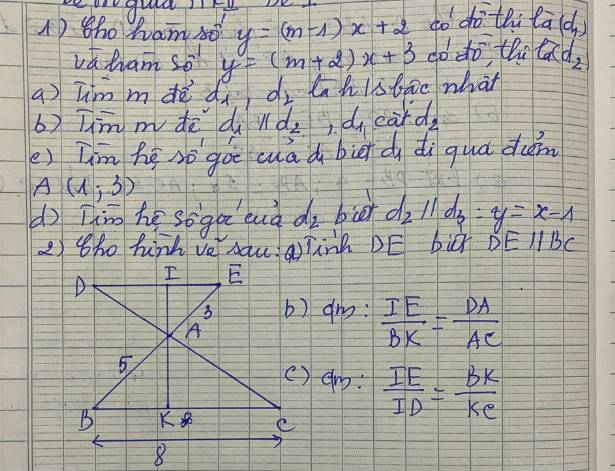





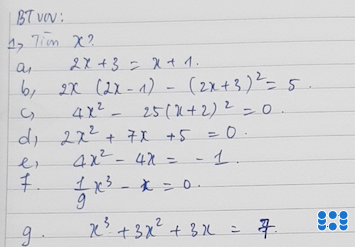
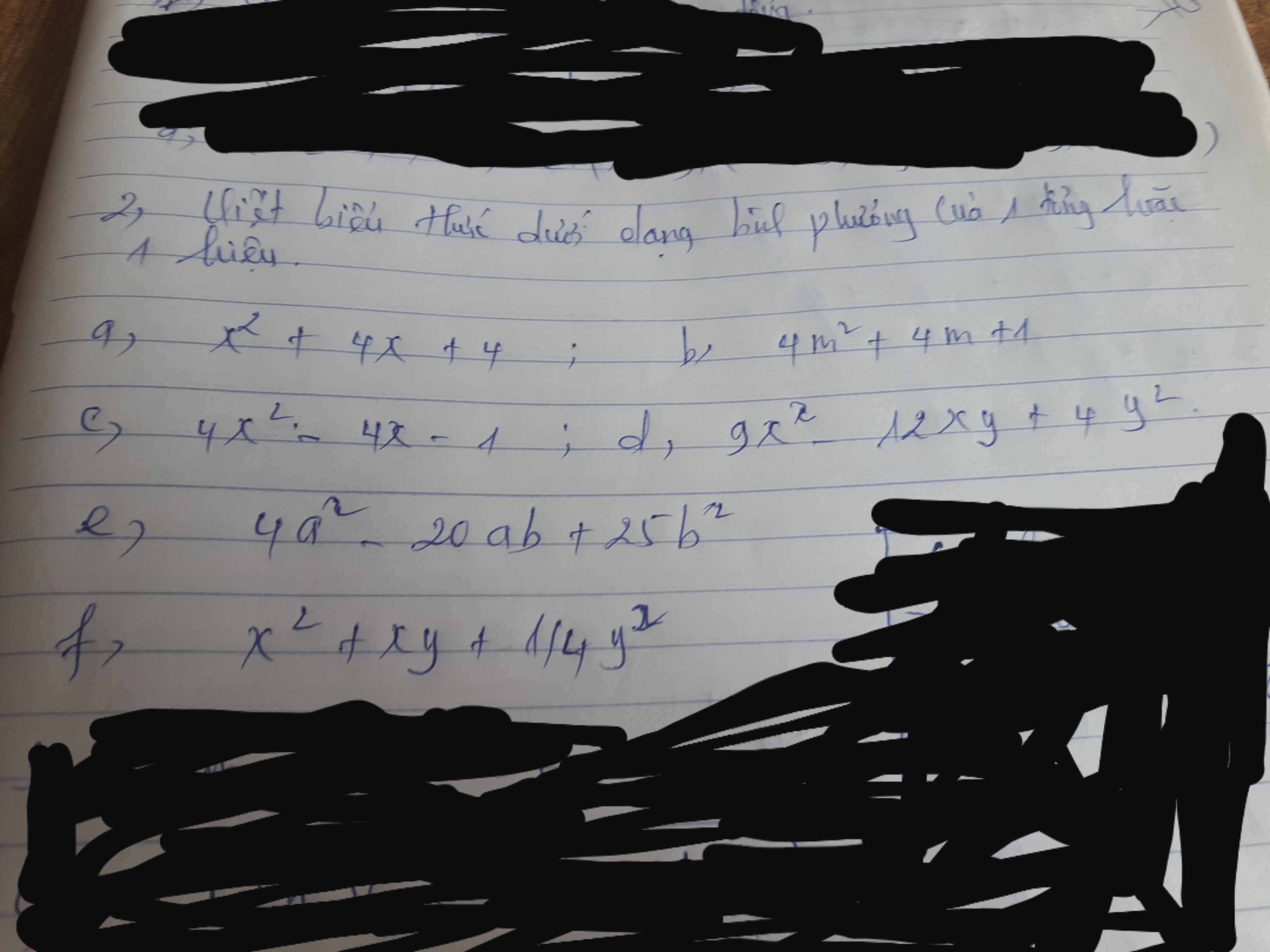

 giải thích giùm mình với
giải thích giùm mình với