Phân thức đại số

c:

Xét tứ giác BKMC có \(\widehat{BKM}=\widehat{BCM}=\widehat{KMC}=90^0\)

nên BKMC là hình chữ nhật

=>BK=MC

Ta có: AK+KB=AB

DM+MC=DC

mà KB=MC và AB=DC

nên AK=DM

Xét ΔCMB vuông tại C và ΔBCA vuông tại B có

\(\widehat{CMB}=\widehat{BCA}\left(=90^0-\widehat{HBC}\right)\)

Do đó: ΔCMB~ΔBCA

=>\(\dfrac{CM}{BC}=\dfrac{CB}{BA}\)

mà CM=KB

nên \(\dfrac{KB}{BC}=\dfrac{BC}{AB}\)

=>\(\dfrac{KI}{AB}=\dfrac{BC}{AB}\)

Xét ΔABC có KI//BC

nên \(\dfrac{AK}{AB}=\dfrac{KI}{BC}\)

=>\(\dfrac{AK}{KI}=\dfrac{AB}{BC}\)

=>\(\dfrac{KI}{KA}=\dfrac{BC}{AB}\)

=>\(\dfrac{KI}{KA}=\dfrac{KB}{AD}\)

mà AK=DM

nên \(\dfrac{KI}{DM}=\dfrac{KB}{DA}\)

Xét ΔDMA vuông tại D và ΔKIB vuông tại K có

\(\dfrac{KI}{DM}=\dfrac{KB}{DA}\)

Do đó: ΔDMA~ΔKIB
=>\(\widehat{DMA}=\widehat{KIB}\)

mà \(\widehat{AMC}=180^0-\widehat{DMA};\widehat{BIM}=180^0-\widehat{KIB}\)

nên \(\widehat{AMC}=\widehat{BIM}\)

Câu 14:

a: Hệ số góc bằng -3 nên a=-3

=>y=-3x+b

Thay x=1 và y=3 vào y=-3x+b, ta được:

\(-3\cdot1+b=3\)

=>b-3=3

=>b=6

Vậy: y=-3x+6

b: Vì đồ thị hàm số y=ax+b song song với đường thẳng y=4x-1 nên \(\left\{{}\begin{matrix}a=4\\b\ne-1\end{matrix}\right.\)

Vậy: y=4x+b

Thay x=-1 và y=4 vào y=4x+b, ta được:

\(4\cdot\left(-1\right)+b=4\)

=>b-4=4

=>b=8

Vậy: y=4x+8

Câu 15:

a: Xét ΔCHM vuông tại H và ΔCDA vuông tại D có

\(\widehat{HCM}\) chung

Do đó: ΔCHM~ΔCDA

b: Xét ΔHCB vuông tại H và ΔBCA vuông tại B có

\(\widehat{HCB}\) chung

Do đó: ΔHCB~ΔBCA

=>\(\dfrac{HC}{BC}=\dfrac{BC}{CA}\)

=>\(BC^2=CH\cdot CA\left(1\right)\)

Ta có: ΔCMH~ΔCAD

=>\(\dfrac{CM}{CA}=\dfrac{CH}{CD}\)

=>\(CH\cdot CA=CM\cdot CD\left(2\right)\)

Từ (1),(2) suy ra \(CM\cdot CD=BC^2\)

=>\(MC=\dfrac{BC^2}{CD}=\dfrac{6^2}{8}=4,5\left(cm\right)\)

Câu 15:

a: Xét ΔAOB và ΔCOD có

\(\widehat{AOB}=\widehat{COD}\)(hai góc đối đỉnh)

\(\widehat{OBA}=\widehat{ODC}\)(hai góc so le trong, BA//CD)

Do đó: ΔAOB~ΔCOD

b: Xét ΔKDH có AE//DH

nên \(\dfrac{AE}{DH}=\dfrac{KE}{KH}=\dfrac{KA}{KD}\left(1\right)\)

Xét ΔKHC có EB//HC

nên \(\dfrac{EB}{HC}=\dfrac{KE}{KH}\left(2\right)\)

Từ (1),(2) suy ra \(\dfrac{AE}{DH}=\dfrac{EB}{HC}\)

=>\(AE\cdot HC=EB\cdot HD\)

c: Xét ΔOAE và ΔOCH có

\(\widehat{OAE}=\widehat{OCH}\)(hai góc so le trong, AE//CH)

\(\widehat{AOE}=\widehat{COH}\)(hai góc đối đỉnh)

Do đó: ΔOAE~ΔOCH

=>\(\dfrac{AE}{CH}=\dfrac{OA}{OC}\left(3\right)\)

Ta có: ΔAOB~ΔCOD

=>\(\dfrac{OA}{OC}=\dfrac{AB}{CD}\left(4\right)\)

Xét ΔKDC có AB//CD

nên \(\dfrac{AB}{CD}=\dfrac{KA}{KD}\left(5\right)\)

Từ (1),(3),(4),(5) suy ra \(\dfrac{AE}{CH}=\dfrac{AE}{DH}\)

=>CH=DH

=>H là trung điểm của CD

Ta có: \(\dfrac{AE}{DH}=\dfrac{EB}{HC}\)

mà HD=HC

nên AE=EB

=>E là trung điểm của AB

=>\(\dfrac{AE}{AB}=\dfrac{1}{2}\)

Câu 13:

Bạn cần hỗ trợ bài nào bạn nên ghi chú rõ ra nhé.

Bài 1

a) (x - 4)/7 + (6x + 4)/7

= (x - 4 + 6x + 4)/7

= 7x/7

= x

b) Đề thiếu

c) (3x - 2)/(x + 1) - (2x - 1)/(x + 1)

= (3x - 2 - x + 1)/(x + 1)

= (2x - 1)/(x + 1)

d) (x + y)/(3x) + (x - 2y)/(3x)

= (x + y + x - 2y)/(3x)

= (2x - y)/(3x)

Bài 2:

a: ĐKXĐ: \(x\notin\left\{1;-1\right\}\)

\(\dfrac{x+1}{2x-2}+\dfrac{-2x}{x^2-1}\)

\(=\dfrac{x+1}{2\left(x-1\right)}-\dfrac{2x}{\left(x-1\right)\left(x+1\right)}\)

\(=\dfrac{\left(x+1\right)^2-4x}{2\left(x-1\right)\left(x+1\right)}\)

\(=\dfrac{\left(x-1\right)^2}{2\left(x-1\right)\left(x+1\right)}=\dfrac{x-1}{2\left(x+1\right)}\)

b: ĐKXĐ: \(x\notin\left\{0;1;-1\right\}\)

\(\dfrac{x^3-1}{x^2-x}-\dfrac{x^3+1}{x^2+x}\)

\(=\dfrac{\left(x-1\right)\left(x^2+x+1\right)}{x\left(x-1\right)}-\dfrac{\left(x+1\right)\left(x^2-x+1\right)}{x\left(x+1\right)}\)

\(=\dfrac{x^2+x+1}{x}-\dfrac{x^2-x+1}{x}\)

\(=\dfrac{x^2+x+1-x^2+x-1}{x}=\dfrac{2x}{x}=2\)

Câu 10:

\(\dfrac{AB}{MK}=\dfrac{BC}{MN}=\dfrac{CA}{KN}\Rightarrow\Delta ABC\sim\Delta KMN\)

\(\rightarrow D\)

Câu 11:

AD là phân giác của tam giác ABC \(\Rightarrow\dfrac{AB}{BD}=\dfrac{AC}{CD}\Rightarrow\dfrac{AB}{BD}=\dfrac{AC}{BC-BD}\)

\(\Rightarrow\dfrac{8}{BD}=\dfrac{12}{10-BD}\Rightarrow80-8BD=12BD\Rightarrow BD=4\left(cm\right)\) 

\(\rightarrow A\) 

Câu 12: 

Ta có: \(\Delta ABC\sim\Delta DEF\) theo hệ số \(k_1\) \(\Rightarrow\dfrac{AB}{DE}=k_1\) 

\(AB=k_1\cdot DE\) 

\(\Delta DEF\sim\Delta MNP\) theo hệ số \(k_2\) \(\Rightarrow\dfrac{DE}{MN}=k_2\)

\(MN=\dfrac{DE}{k_2}\) 

Khi đó \(\Delta MNP\sim\Delta ABC\) theo hệ số: \(\dfrac{MN}{AB}=\dfrac{\dfrac{DE}{k_2}}{DE\cdot k_1}=\dfrac{\dfrac{1}{k^2}}{k_1}=\dfrac{1}{k_1\cdot k_2}\)

\(\rightarrow A\)

Bài 16:

Ta có: \(A=\dfrac{x^2-6xy+6y^2}{x^2-2xy+y^2}\)

\(=\dfrac{-3x^2+6xy-3y^2+4x^2-12xy+9y^2}{x^2-2xy+y^2}\)

\(=\dfrac{-3\left(x^2-2xy+y^2\right)+\left(4x^2-12xy+9y^2\right)}{x^2-2xy+y^2}\)

\(=\dfrac{-3\left(x^2-2xy+y^2\right)}{x^2-2xy+y^2}+\dfrac{\left(2x\right)^2-2\cdot2x\cdot3y+\left(3y\right)^2}{x^2-2xy+y^2}\)

\(=-3+\dfrac{\left(2x-3y\right)^2}{\left(x-y\right)^2}\)

Ta có: \(\dfrac{\left(2x-3y\right)^2}{\left(x-y\right)^2}\ge0\forall x\ne y\Rightarrow A=-3+\dfrac{\left(2x-3y\right)^2}{\left(x-y\right)^2}\ge-3\)

Dấu "=" xảy ra khi: \(2x-3y=0\Leftrightarrow x=\dfrac{3}{2}y\) 

Vậy: \(A_{min}=-3\Leftrightarrow x=\dfrac{3}{2}y\)

Câu 1: A

Câu 2: C

Câu 3: D

Câu 4: B

Câu 5: C

Câu 6: D

Câu 7: B

Câu 8: D

Câu 9: A

Bài 16: 

Ta có: 

\(Q=\dfrac{5x^2-24x+29}{x^2-4x+4}\left(x\ne2\right)\)

\(Q=\dfrac{x^2-4x+4+4x^2-20x+25}{x^2-4x+4}\)

\(Q=\dfrac{x^2-4x+4}{x^2-4x+4}+\dfrac{4x^2-20x+25}{x^2-4x+4}\)

\(Q=1+\dfrac{\left(2x\right)^2-2\cdot2x\cdot5+5^2}{x^2-2\cdot x\cdot2+2^2}\)

\(Q=1+\dfrac{\left(2x-5\right)^2}{\left(x-2\right)^2}\)

Mà: \(\dfrac{\left(2x-5\right)^2}{\left(x-2\right)^2}\ge0\forall x\ne2\)

\(\Rightarrow Q=1+\dfrac{\left(2x-5\right)^2}{\left(x-2\right)^2}\ge1\forall x\ne2\)

Dấu "=" xảy ra: \(\left(2x-5\right)^2=0\Leftrightarrow2x-5=0\Leftrightarrow x=\dfrac{5}{2}\left(tm\right)\)

Vậy: \(Q_{min}=1\Leftrightarrow x=\dfrac{5}{2}\)

Câu 14:

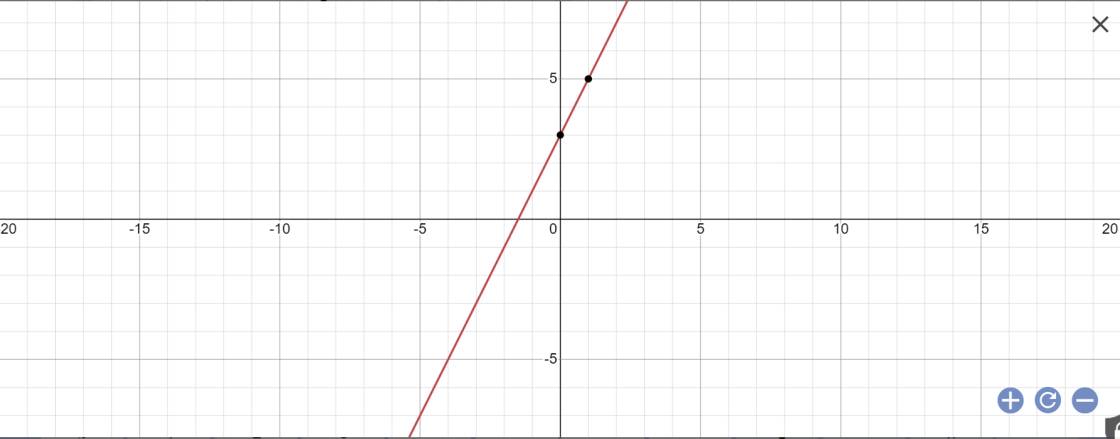
a: Thay x=2 và y=7 vào y=2x+b, ta được:

\(b+2\cdot2=7\)

=>b+4=7

=>b=3

=>y=2x+3

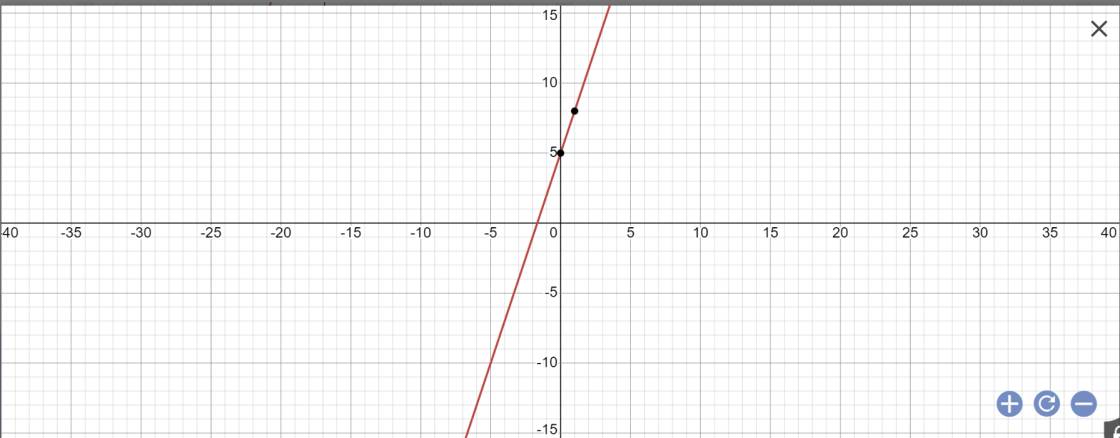
b: Thay x=-2 và y=-1 vào y=ax+5, ta được:

-2a+5=-1

=>-2a=-6

=>a=3

=>y=3x+5

Câu 15:

a: Xét ΔABC vuông tại A và ΔHBA vuông tại H có

\(\widehat{ABC}\) chung

Do đó: ΔABC~ΔHBA

b: Xét ΔHBA vuông tại H và ΔHAC vuông tại H có

\(\widehat{HBA}=\widehat{HAC}\left(=90^0-\widehat{HAB}\right)\)

Do đó: ΔHBA~ΔHAC

=>\(\dfrac{HB}{HA}=\dfrac{HA}{HC}\)

=>\(HA^2=HB\cdot HC\)

c:

Xét ΔABC vuông tại A có AH là đường cao

nên \(AH^2=HB\cdot HC\)

=>\(AH^2=4\cdot16=64\)

=>\(AH=\sqrt{64}=8\left(cm\right)\)

Xét tứ giác ADHE có \(\widehat{ADH}=\widehat{AEH}=\widehat{DAE}=90^0\)

nên ADHE là hình chữ nhật

=>AH=DE

mà AH=8cm

nên DE=8cm