Câu 2:
a: Xét ΔABC có AD là phân giác
nên \(\dfrac{DB}{AB}=\dfrac{DC}{AC}\)
=>\(\dfrac{DB}{15}=\dfrac{DC}{20}\)
=>\(\dfrac{DB}{3}=\dfrac{DC}{4}\)
mà DB+DC=BC=25cm
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{DB}{3}=\dfrac{DC}{4}=\dfrac{DB+DC}{3+4}=\dfrac{25}{7}\)
=>\(DB=\dfrac{25}{7}\cdot3=\dfrac{75}{7}\left(cm\right);DC=\dfrac{25}{7}\cdot4=\dfrac{100}{7}\left(cm\right)\)
Xét ΔCAB có ED//AB
nên \(\dfrac{ED}{AB}=\dfrac{CD}{CB}\)
=>\(\dfrac{ED}{15}=\dfrac{4}{7}\)
=>\(ED=\dfrac{4}{7}\cdot15=\dfrac{60}{7}\left(cm\right)\)
b: Xét ΔABC có \(AB^2+AC^2=BC^2\)
nên ΔABC vuông tại A
=>\(S_{ABC}=\dfrac{1}{2}\cdot AB\cdot AC=\dfrac{1}{2}\cdot15\cdot20=10\cdot15=150\left(cm^2\right)\)
Xét ΔABC có AH là đường cao
nên \(S_{ABC}=\dfrac{1}{2}\cdot AH\cdot BC\)
=>\(AH\cdot25=2\cdot150=300\)
=>\(AH=\dfrac{300}{25}=12\left(cm\right)\)
c: Ta có: \(\dfrac{BD}{BC}=\dfrac{75}{7}:25=\dfrac{3}{7}\)
=>\(S_{ABD}=\dfrac{3}{7}\cdot S_{ABC}=\dfrac{3}{7}\cdot150=\dfrac{450}{7}\left(cm^2\right)\)
=>\(S_{ACD}=S_{ABC}-S_{ABD}=150-\dfrac{450}{7}=\dfrac{600}{7}\left(cm^2\right)\)
Xét ΔCAB có ED//AB
nên \(\dfrac{CE}{CA}=\dfrac{ED}{AB}=\dfrac{CD}{CB}=\dfrac{4}{7}\)
=>\(S_{CED}=\dfrac{4}{7}\cdot S_{CAD}=\dfrac{4}{7}\cdot\dfrac{600}{7}=\dfrac{2400}{49}\left(cm^2\right)\)
Ta có: \(S_{CDE}+S_{AED}=S_{CAD}\)
=>\(S_{AED}=\dfrac{3}{7}\cdot S_{CAD}=\dfrac{3}{7}\cdot\dfrac{600}{7}=\dfrac{1800}{49}\left(cm^2\right)\)
Bài 1:
a: 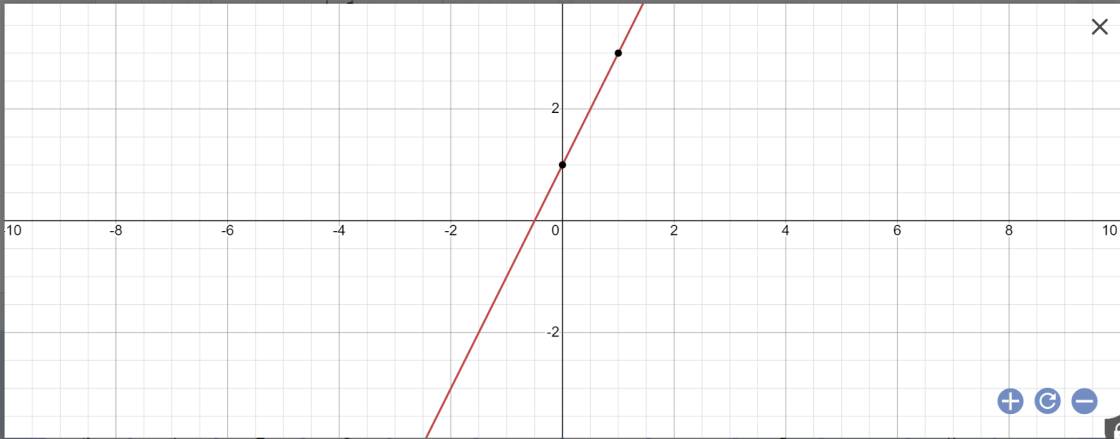
b: Để (d1)//(d2) thì \(\left\{{}\begin{matrix}m-2=2\\m\ne1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m=4\\m\ne1\end{matrix}\right.\)
=>m=4
c: Thay x=2 và y=-3 vào (d1), ta được:
\(2\left(m-2\right)+m=-3\)
=>2m-4+m=-3
=>3m=-3+4=1
=>\(m=\dfrac{1}{3}\)
d: Để (d1) cắt (d2) tại một điểm trên trục tung thì
\(\left\{{}\begin{matrix}m-2\ne2\\m=1\end{matrix}\right.\)
=>m=1






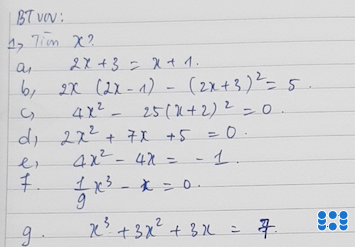
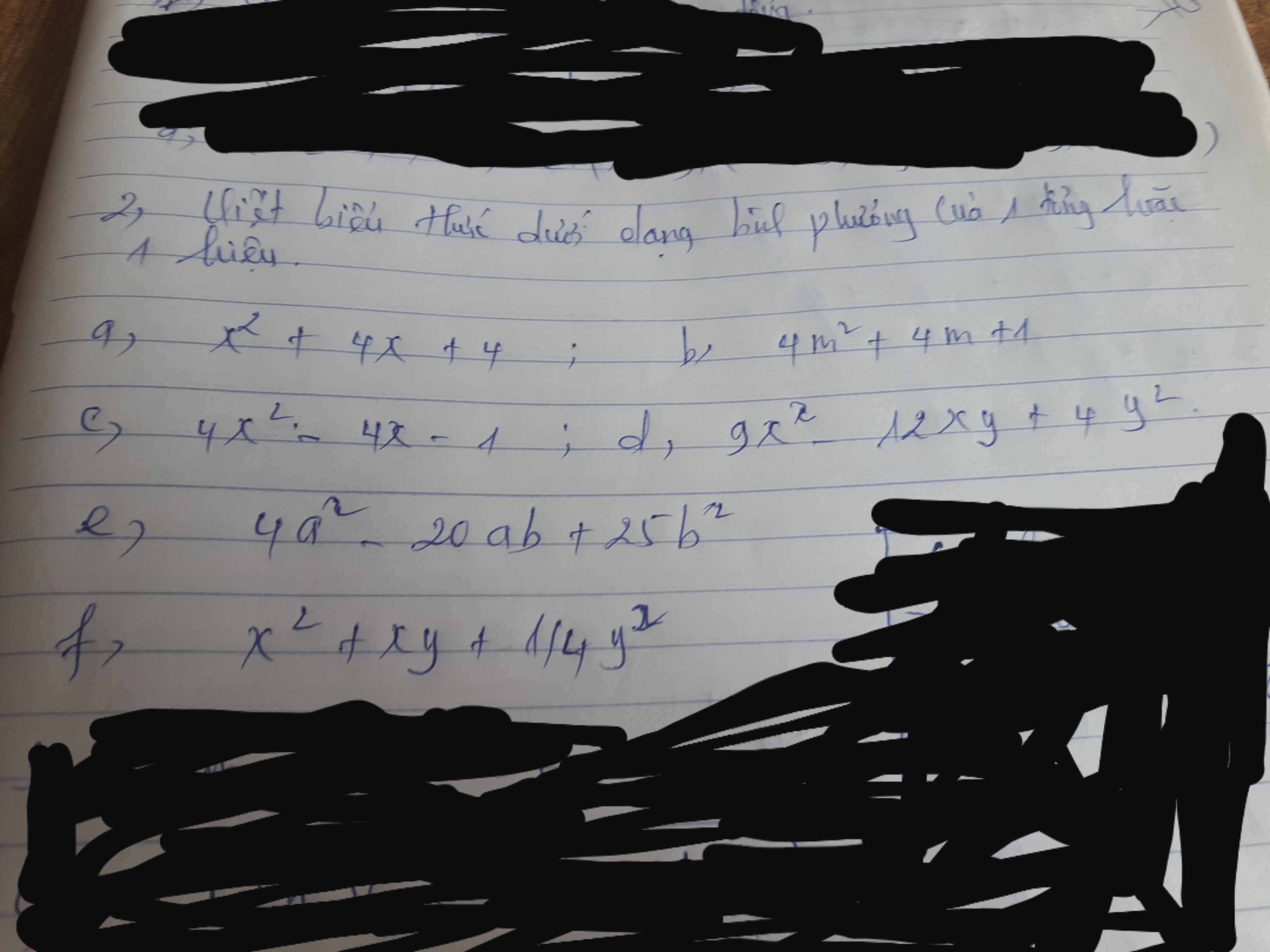

 giải thích giùm mình với
giải thích giùm mình với