Cho hai hàm số y=x^2 (dm) và y=(m-1)x +m+1 có đồ thị là P (m là tham số). Tìm m nguyên dương để (dm) cắt (P) tại điểm có tọa độ nguyên
Ôn tập chương 2: Hàm số bậc nhất
Lời giải:
PT hoành độ giao điểm:
$x^2-(m-1)x-m-1=0(*)$
Để $(P)$ và $(dm)$ cắt nhau tại 1 điểm có tọa độ nguyên thì PT $(*)$ phải có nghiệm nguyên
Điều này xảy ra khi $\Delta=(m-1)^2+4(m+1)=a^2$ với $a$ là số tự nhiên
$\Leftrightarrow m^2+2m+5=a^2$
$\Leftrightarrow (m+1)^2+4=a^2$
$\Leftrightarrow 4=(a-m-1)(a+m+1)$
Vì $a+m+1>0$ và $a+m+1> a-m-1$ với mọi $a$ tự nhiên, $m$ nguyên dương nên:
$a+m+1=4; a-m-1=1$
$\Rightarrow m=\frac{1}{2}$ (vô lý)
Vậy không tồn tại $m$ thỏa mãn điều kiện đề bài.
Đúng 0
Bình luận (0)
9B. Cho parabol (P) : y = 1/2 x^2
a) Vẽ (P) trên mặt phẳng tọa độ.
b) Dựa vào đồ thị hãy biện luận theo m số nghiệm của phương trình x2
– 2m + 4=0
giúp tui làm câu b ạ
a:
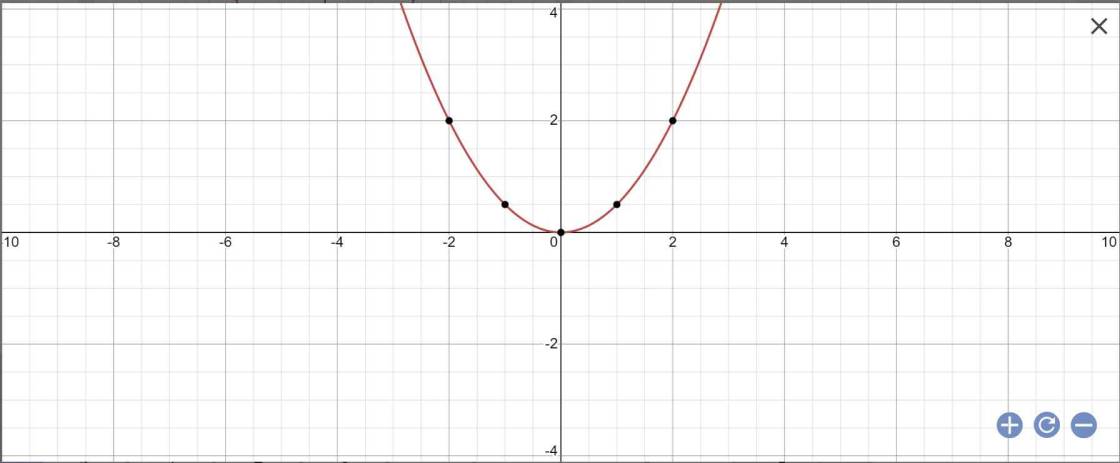
b: \(\Delta=\left(-2m\right)^2-4\cdot1\cdot4=4m^2-16\)
Để phương trình có hai nghiệm phân biệt thì 4m^2-16>0
=>m>2 hoặc m<-2
Để phương trình có nghiệm duy nhất thì 4m^2-16=0
=>m=2 hoặc m=-2
Để phương trìh vô nghiệm thì 4m^2-16<0
=>-2<m<2
Đúng 1
Bình luận (0)
tìm m để đồ thị hàm số y=2x+1 cắt đồ thị hàm số y=(m+1)x
`y=2x+1` cắt `y=(m+1)x<=>a \ne a'`
`<=>2 \ne m+1<=>m \ne 1`
Đúng 2
Bình luận (0)
Tìm m và k để: y=(m+1)x + k - 3 và y=(3-m)x + 1 - k là 2 đường thẳng song song nhau
2 đường thẳng đã cho song song khi:
\(\left\{{}\begin{matrix}m+1=3-m\\k-3\ne1-k\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}m=1\\k\ne2\end{matrix}\right.\)
Đúng 2
Bình luận (0)
Cho (d): y= (m-1)x + m (d1): y= 2x - 3 Vẽ (d) và (d1) với m=3 và tính khoảng cách (d) và (d1)
Khi m=3 thì (d): y=2x+3
Lấy A(0;3) thuộc (d)
(d1): y=2x-3
=>2x-y-3=0
\(h\left(A;d1\right)=\dfrac{\left|0\cdot2+\left(-1\right)\cdot3+\left(-3\right)\right|}{\sqrt{2^2+1^2}}=\dfrac{6}{\sqrt{5}}\)
Đúng 0
Bình luận (0)
Tìm tất cả giá trị của m để khoảng cách từ gốc tọa độ đến (d):y=(m-2)x + 3 bằng 1
\(d\left(O;d\right)=\dfrac{\left|\left(m-2\right)\cdot0+\left(-1\right)\cdot0+3\right|}{\sqrt{\left(m-2\right)^2+1}}=\dfrac{3}{\sqrt{\left(m-2\right)^2+1}}\)
Để d=1 thì \(\sqrt{\left(m-2\right)^2+1}=3\)
=>(m-2)^2+1=9
=>(m-2)^2=8
=>\(m=\pm2\sqrt{2}+2\)
Đúng 1
Bình luận (0)
a vẽ các ĐTHS y=x(d1) y=2x+2(d2) trên cùngmp
b gọi A là giao điểm của hai đồ thị tìm tọa độ A
c tìm m để y=(m+3)x-5 đi qua A
d tìm m để d2 cắt đường thẳng y=(2m-1)x+m tai 1 điểm trên trục tung
giúp mk vs
b: Tọa độ A là:
2x+2=x và y=x
=>x=-2 và y=-2
c: Thay x=-2 và y=-2 vào (d), ta đc:
(m+3)*(-2)-5=-2
=>(m+3)*(-2)=3
=>m+3=-3/2
=>m=-9/2
Đúng 0
Bình luận (0)
Giúp mình bài 2 với ạ
Câu 2:
a) Vì (d) cắt trục tung tại điểm có tung độ bằng 3:
\(\Rightarrow3=\left(m+2\right).0+2m^2+1\)
\(\Leftrightarrow m^2=1\)
\(\Leftrightarrow m=\pm1\) (nhận)
Với \(m=1\Rightarrow y=\left(1+2\right)x+2.1^2+1\Rightarrow y=3x+3\).
Bảng giá trị:
x -1 0
\(y=3x+3\) 0 3
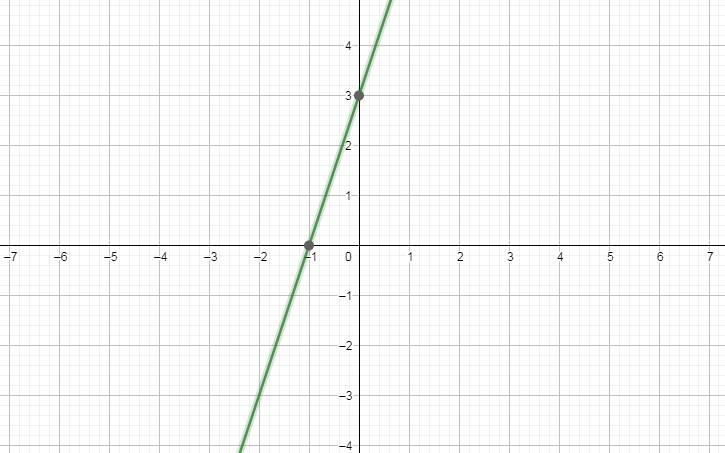
Với \(m=-1\Rightarrow y=\left(-1+2\right)x+2.\left(-1\right)^2+1=x+3\)
Bảng giá trị:
x -3 0
\(y=x+3\) 0 3
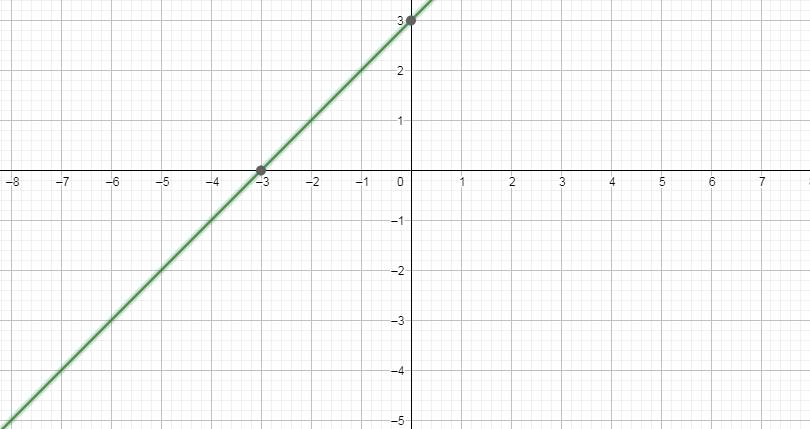
Đúng 1
Bình luận (0)
Câu 2:
b) Gọi \(A\left(x_0;y_0\right)\) là tọa độ giao điểm của (d) và (d'). Vì A nằm trên trục tung Oy \(\Rightarrow A\left(0;y_0\right)\).
- Thay \(A\left(0;y_0\right)\) vào pt \(\left(d\right):y=\left(m+2\right)x+2m^2+1\) ta được:
\(y_0=\left(m+2\right).0+2m^2+1\Rightarrow y_0=2m^2+1\left(1\right)\)
- Thay \(A\left(0;y_0\right)\) vào pt \(\left(d'\right):y=\left(2m+2\right)x-m+1\)
\(y_0=\left(2m+2\right).0-m+1\Rightarrow y_0=-m+1\left(2\right)\)
Từ (1), (2) ta có: \(2m^2+1=-m+1\)
\(\Leftrightarrow2m^2+m=0\)
\(\Leftrightarrow m\left(2m+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}m=0\\m=-\dfrac{1}{2}\end{matrix}\right.\)
c) Gọi B là giao của (d) và trục hoành Ox \(\Rightarrow B\left(x_1;0\right)\) (x1 là số nguyên).
Thay \(B\left(x_1;0\right)\) vào pt \(\left(d\right):y=\left(m+2\right)x+2m^2+1\) ta được:
\(0=\left(m+2\right)x_1+2m^2+1\)
\(\Rightarrow x_1=-\dfrac{2m^2+1}{m+2}=-\dfrac{2\left(m^2-4\right)+9}{m+2}=-\dfrac{2\left(m-2\right)\left(m+2\right)+9}{m+2}=-2\left(m-2\right)-\dfrac{9}{m+2}\)Để x1 là số nguyên thì \(9⋮\left(m+2\right)\)
\(\Rightarrow m+2\inƯ\left(9\right)\)
\(\Rightarrow m+2\in\left\{1;-1;9;-9\right\}\)
\(\Rightarrow m\in\left\{-1;-3;7;-11\right\}\)
Đúng 0
Bình luận (0)
Bài 10: Chứng tỏ đường thẳng y = mx - 2m + 1 luôn đi qua một điểm cố định khi m thay đổi.
y=m(x-2)+1
=>m(x-2)-y+1=0
Điểm mà (d) luôn đi qua có tọa độ là:
x-2=0 và 1-y=0
=>x=2 và y=1
Đúng 1
Bình luận (0)
Cho hàm số y = (m - 2) * x + m + 3
a) Tìm điều kiện của m để hàm số luôn luôn nghịch biến .
b) Tìm điều kiện của m để đồ thị cắt trục hoành tại điểm có hoành độ bằng 3. c) Tìm m để đồ thị hàm số y = - x + 2 . y = 2x - 1 và y = (m - 2) * x + m + 3 đồng quy.
d)Tìm m để đồ thị hàm số tạo với trục tung và trục hoành một tam giác có diện tích bằng 2
a: Để hàm số nghịch biên thì m-2<0
=>m<2
b: Thay x=3 và y=0 vào (d), ta đc:
3(m-2)+m+3=0
=>3m-6+m+3=0
=>4m-3=0
=>m=3/4
c: Tọa độ giao điểm là
2x-1=-x+2 và y=-x+2
=>x=1 và y=1
Thay x=1 và y=1 vào (d), ta được:
m-2+m+3=1
=>2m+1=1
=>m=0
Đúng 2
Bình luận (0)




