Bài 6. Cho đường thẳng (d1): y = 3x - 2 Viết phương trình đường thẳng (d) đi qua điêm A(1; 3) và cắt đường thẳng (d) tại điểm có hoành độ bằng 2.
Ôn tập chương 2: Hàm số bậc nhất
Gọi `(d): y=ax+b`
Thay `x=2` vào `(d_1)` có: `y=3.2-2=4`
`=>` Thay `A(1;3)` và `(2;4)` vào `(d)` có hệ ptr:
`{(3=a+b),(4=2a+b):}`
`<=>{(a=1),(1+b=3):}<=>{(a=1),(b=2):}`
`=>(d): y=x+2y`
Đúng 2
Bình luận (1)
Bài 8. Cho các đường thẳng (d1) : y 4mx - (m+5) với m≠0 =
(d_{2}) / y = (3m ^ 2 + 1) * x + (m ^ 2 - 9)
a) Với giá trị nào của m thì (di) song song với đường thẳng (d2)
b) Với giá trị nào của m thì (d1) cắt (d2) tìm toạ độ giao điểm khi m = 2
c) C/m rằng khi m thay đổi thì đường thẳng (d1) luôn đi điểm cố định A.
a: Để hai đường song song thì \(\left\{{}\begin{matrix}3m^2+1=4m\\-m-5< >m^2-9\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3m^2-4m+1=0\\m^2-9+m+5< >0\end{matrix}\right.\)
\(\Leftrightarrow m\in\left\{1;\dfrac{1}{3}\right\}\)
b: Khi m=2 thì (d1): y=8x-7
(d2): \(y=\left(3\cdot2^2+1\right)\cdot x+\left(2^2-9\right)=13x-5\)
Tọa độ giao điểm là:
13x-5=8x-7 và y=8x-7
=>x=-2/5 và y=-16/5-7=-51/5
Đúng 1
Bình luận (0)
Bài 7. Cho (d1): y = 3x và (d2): y=x+2
a) Vẽ (dı) và (d2) trên cùng hệ trục tọa độ.
b) Cho (d3): y = ax + b. Tìm a, b biết (d3) song song với (d2) và qua A(−1 ; 2)
b: Vì (d3)//(d2) nên (d3): y=x+b
Thay x=-1 và y=2 vào (d3), ta được:
b-1=2
=>b=3
Đúng 1
Bình luận (1)
Một chiếc máy bay bay lên với vận tốc 600km/h. Sau 2 phút máy bay đạt độ cao BC =8500m. Khi đó thì góc A tạo bởi đường bay lên và phương nằm ngang là bao nhiêu độ?
Xem chi tiết

Lời giải:
Sau 2 phút bay máy bay đi được quãng đường:
$AC=600:60.2=20$ (km)
Đổi $20$ km = $20000$ m
Có: $\sin A = \frac{CB}{CA}=\frac{8500}{20000}=\frac{17}{40}$
$\Rightarrow \widehat{A}\approx 25,15^0$
Đúng 0
Bình luận (0)
Mình cần gấp bài 3 nha mọi người
giúp em bài nài với ạ
a: Để hai đường song song thì
\(\left\{{}\begin{matrix}m^2-2m+5=m+3\\m< >2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m^2-3m+2=0\\m< >2\end{matrix}\right.\Leftrightarrow m=1\)
b: Tọa độ A là:
y=0 và (m^2-2m+5)x+2=0
=>x=-2/m^2-2m+5 và y=0
Tọa độ B là:
x=0 và y=0(m^2-2m+5)+2=2
=>OB=2; OA=2/m^2-2m+5
\(S_{OAB}=\dfrac{1}{2}\cdot OA\cdot OB=\dfrac{1}{2}\cdot2\cdot\dfrac{2}{m^2-2m+5}=\dfrac{2}{m^2-2m+5}\)
Để S lớn nhất thì m^2-2m+5 nhỏ nhất
=>(m-1)^2+4 nhỏ nhất
=>(m-1)^2+4=4
=>m=1
Đúng 0
Bình luận (0)
giup em bai nay vs a !!
a: Thay x=0 và y=0 vào (1), ta được:
m-1=0
=>m=1
b: 2-m=tan30=căn 3/3
nên \(m=\dfrac{6-\sqrt{3}}{3}\)
c: \(2-m=tan135=-1\)
=>m=3
d: Thay x=0 và y=4 vào (d), ta được:
m-1=4
=>m=5
Đúng 2
Bình luận (0)
Cho hai hàm số y = 2x + 5 và y = -3x có đồ thị lần lượt là (d1) và (d2)
Vẽ hai đồ thị (d1) và (d2) trên cùng một mặt phẳng tọa độ
Anh em giúp tôi câu B với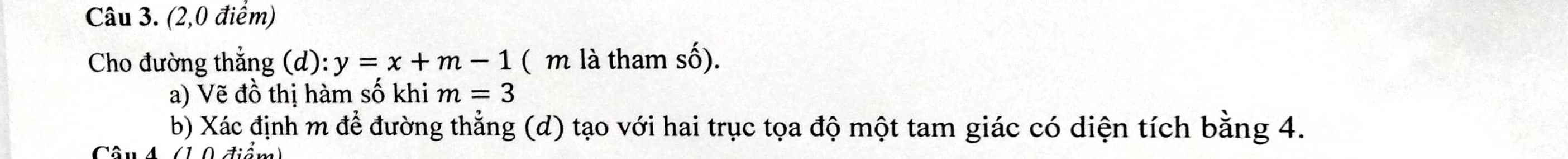
b: Gọi A,B lần lượt là giao của (d) với trục Ox,Oy
=>A(-m+1;0); B(0;m-1)
=>OA=|m-1|; OB=|m-1|
Theo đề, ta có: 1/2*OA*OB=4
=>(m-1)^2=8
=>\(m=\pm2\sqrt{2}+1\)
Đúng 1
Bình luận (1)
Cho đường thẳng (d) : y = 2x - 5 a) Tính góc a tạo bởi (d) và Ox b) gọi (d) cắt Ox tại A, cắt Oy tại B .Tính S∆OAB c) Tính khoảng cách từ O đến (d)
a: tan a=2
nên a=63 độ
b: Tọa độ A là:
y=0 và 2x-5=0
=>x=2,5; y=0
=>OA=2,5
Tọa độ B là:
x=0 và y=2*0-5=-5
=>OB=5
\(S_{OAB}=\dfrac{2.5\cdot5}{2}=6.25\)
c: \(AB=\sqrt{5^2+2.5^2}=\dfrac{5}{2}\sqrt{5}\)
\(d\left(O;\left(d\right)\right)=\dfrac{5\cdot2.5}{2.5\sqrt{5}}=\dfrac{5}{\sqrt{5}}=\sqrt{5}\)
Đúng 0
Bình luận (0)


