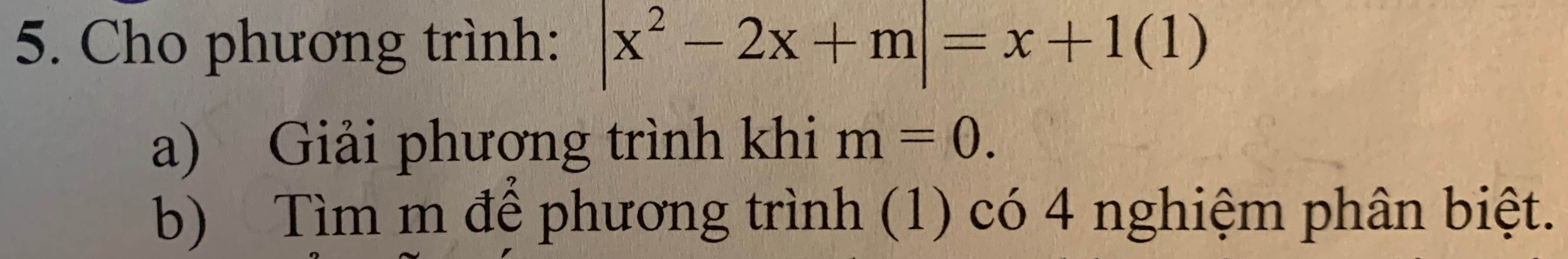a, Với $m=0$ phương trình $(1)$ trở thành:
$|x^2-2x|=x+1$
\(\Leftrightarrow\left[{}\begin{matrix}x^2-2x=x+1\\x^2-2x=-x-1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x^2-3x=1\\x^2-x+1=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}4x^2-12x+9=13\\\left(x-\dfrac{1}{2}\right)^2+\dfrac{3}{4}=0\left(loại\right)\end{matrix}\right.\)
\(\Rightarrow\left(2x-3\right)^2=13\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\sqrt{13}+3}{2}\\x=\dfrac{-\sqrt{13}+3}{2}\end{matrix}\right.\)
b, $pt(1)⇔$ \(\left[{}\begin{matrix}x^2-2x+m=x+1\\x^2-2x+m=-x-1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x^2-3x+m-1=0\\x^2-x+m+1=0\end{matrix}\right.\)
Nên để pt (1) có 4 nghiệm phân biệt thì 2 phương trình trên phải có 2 nghiệm phân biệt tức $\triangle$ mỗi phương trình phải $>0$
tức là \(\left[{}\begin{matrix}\left(-3\right)^2-4.1.\left(m-1\right)>0\\\left(-1\right)^2-4.1\left(m+1\right)>0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}4m< 5\\4m< -3\end{matrix}\right.\Leftrightarrow m< \dfrac{-3}{4}\)
Vậy $m<\dfrac{-3}{4}$ t/m đề