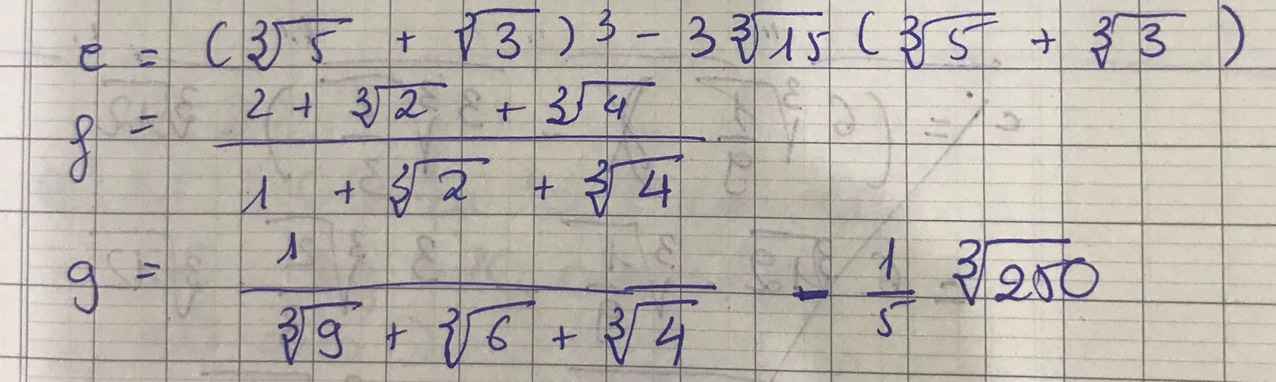Giúp e vs=(
Bài 9: Căn bậc ba
`C_2:`
`a)\sqrt{x^2+6x+9}=5`
`<=>\sqrt{(x+3)^2}=5`
`<=>|x+3|=5`
`<=>[(x+3=5),(x+3=-5):}<=>[(x=2),(x=-8):}`
~~~~~~~~~~~~~~
Có vẻ đề phải là: `\sqrt{9x-9}?`
`b)\sqrt{16x-16}-\sqrt{9x-9}+\sqrt{4x-4}+\sqrt{x-1}=8` `ĐK: x >= 1`
`<=>4\sqrt{x-1}-3\sqrt{x-1}+2\sqrt{x-1}+\sqrt{x-1}=8`
`<=>4\sqrt{x-1}=8`
`<=>\sqrt{x-1}=2`
`<=>x-1=4<=>x=5` (t/m)
_______________________________________________
`C_3:`
`a)A` xác định `<=>{(x > 0),(\sqrt{x}-1 \ne 0),(\sqrt{x}-2 \ne 0):}<=>{(x > 0),(x \ne 1,x \ne 2):}`
Với `x > 0,x \ne 1,x \ne 2` có:
`A=(1/[\sqrt{x}-1]-1/\sqrt{x}):([\sqrt{x}+1]/[\sqrt{x}-2]-[\sqrt{x}+2]/[\sqrt{x}-1])`
`A=[\sqrt{x}-\sqrt{x}+1]/[\sqrt{x}(\sqrt{x}-1)]:[(\sqrt{x}+1)(\sqrt{x}-1)-(\sqrt{x}+2)(\sqrt{x}-2)]/[(\sqrt{x}+2)(\sqrt{x}-1)]`
`A=1/[\sqrt{x}(\sqrt{x}-1)].[(\sqrt{x}+2)(\sqrt{x}-1)]/[x-1-x+4]`
`A=1/\sqrt{x} .[\sqrt{x}+2]/3`
`A=[\sqrt{x}+2]/[3\sqrt{x}]`
~~~~~~~~~~~~~~~~~~~~~~
`b)` Với `x > 0,x \ne 1,x \ne 2` có:
`A=1/4<=>[\sqrt{x}+2]/[3\sqrt{x}]=1/4`
`<=>4\sqrt{x}+8=3\sqrt{x}`
`<=>\sqrt{x}=-8` (Vô lí)
`=>` Ko có gtr của `x` t/m
Đúng 0
Bình luận (0)
Giúp em vs ạ
`1)` Căn thức có nghĩa `<=>1/2x-3 >= 0`
`<=>1/2x >= 3<=>x >= 6`
__________________________________________
`2)`
`a)\sqrt{12}+\sqrt{48}-\sqrt{27}+3\sqrt{47}`
`=2\sqrt{3}+4\sqrt{3}-3\sqrt{3}+3\sqrt{47}`
`=3\sqrt{3}+3\sqrt{47}`
~~~~~~~~~~~~
`b)3/2\sqrt{6}+\sqrt{2/3}-5\sqrt{3/2}`
`=3/2\sqrt{6}+1/3\sqrt{6}-5/2\sqrt{6}`
`=-2/3\sqrt{6}`
~~~~~~~~~~~~
`c)\root[3]{-125}+\root[3]{343}-\root[3]{64}`
`=-5+7-4`
`=-2`
Đúng 0
Bình luận (0)
tìm gtln của biểu thức:
Đọc tiếp
tìm gtln của biểu thức:
\(D=\dfrac{1-x-\sqrt{x^3}}{\sqrt{x}+1}\) \(\left(x\ge0\right)\)
\(D=\dfrac{1-x-x\sqrt{x}}{\sqrt{x}+1}\)
\(D=\dfrac{1-x\left(1+\sqrt{x}\right)}{\sqrt{x}+1}\)
\(D=-\dfrac{x\left(1+\sqrt{x}\right)}{\sqrt{x}+1}+\dfrac{1}{\sqrt{x}+1}\)
\(D=-x+\dfrac{1}{\sqrt{x}+1}\)
Đúng 2
Bình luận (0)
1. a) 2√5-5√2 và 1; b) √8/3 và 3/4.
a: \(2\sqrt{5}-5\sqrt{2}< 0< 1\)
b: \(\sqrt{\dfrac{8}{3}}=\dfrac{2\sqrt{2}}{\sqrt{3}}=\dfrac{2\sqrt{6}}{3}< \dfrac{3}{4}\)
Đúng 2
Bình luận (0)
tìm x biết x=\(\sqrt[3]{16-\sqrt{255}}+\dfrac{1}{\sqrt[3]{16-\sqrt{255}}}\)
\(x=\sqrt[3]{16-\sqrt{255}}+\sqrt[3]{16+\sqrt{255}}\)
\(\Leftrightarrow x^3=16+16+3\cdot x\)
=>x3-3x-32=0
=>\(x\simeq3.49\)
Đúng 2
Bình luận (0)
\(\dfrac{\sqrt[3]{x^2y}-\sqrt[3]{xy^2}}{x\sqrt[3]{y}+y\sqrt[3]{x}}:\left(1-\dfrac{2\sqrt[3]{xy}}{\sqrt[3]{x^2}+\sqrt[3]{y^2}}\right)\) rút gọn
Giải phương trình sau:
\(\sqrt[3]{x^3+2x^2}=x+2\)
⇔ $x^{2}.(x+2)=(x+2)^{3}$
⇔$4(x+1)(x+2)=0$
→$x=-1 hoặc x=-2$
Đúng 0
Bình luận (0)
P/t \(\Leftrightarrow\sqrt[3]{x^2\left(x+2\right)}=x+2\)
\(\Leftrightarrow\left(x+2\right)\left(\sqrt[3]{x^2}-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-2\\x=\pm1\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Lời giải:
ĐKXĐ: $x\in\mathbb{R}$
PT $\Leftrightarrow x^3+2x^2=(x+2)^3$
$\Leftrightarrow x^2(x+2)-(x+2)^3=0$
$\Leftrightarrow (x+2)[x^2-(x+2)^2]=0$
$\Leftrightarrow (x+2)(x-x-2)(x+x+2)=0$
$\Leftrightarrow (x+2)(-2).2(x+1)=0$
$\Leftrightarrow (x+2)(x+1)=0$
$\Leftrightarrow x+2=0$ hoặc $x+1=0$
$\Leftrightarrow x=-2$ hoặc $x=-1$
Đúng 1
Bình luận (0)
Bài tập: Thực hiện phép tính:
a) \(\left(\sqrt[3]{25}-\sqrt[3]{10}+\sqrt[3]{4}\right)\left(\sqrt[3]{5}+\sqrt[3]{2}\right)\)
b) \(\sqrt[3]{\left(4-2\sqrt[3]{3}\right)\left(\sqrt[3]{3}-1\right)}\)
c) \(\sqrt[3]{3+\sqrt{3}+\sqrt[3]{10}+6\sqrt{3}}\)
a: \(=\left(\sqrt[3]{5}\right)^3+\left(\sqrt[3]{2}\right)^3=5+2=7\)
b: \(=\sqrt[3]{\left(\sqrt[3]{3}-1\right)^3}=\sqrt[3]{3}-1\)
Đúng 1
Bình luận (1)
\(f=\dfrac{\sqrt[3]{2}\left(\sqrt[3]{4}+\sqrt[3]{2}+\sqrt[3]{1}\right)}{\sqrt[3]{1}+\sqrt[3]{2}+\sqrt[3]{4}}=\sqrt[3]{2}\)
e: \(=5+3+3\sqrt[3]{75}+\sqrt[3]{45}-3\sqrt[3]{75}-3\sqrt[3]{45}=8\)
Đúng 0
Bình luận (0)
e: =>x+4+1-x-2căn (x+4)(1-x)=1-2x
=>2căn (x+4)(1-x)=5-1+2x=2x+4
=>căn (x+4)(1-x)=x+2
=>(x+4)(1-x)=x^2+4x+4 và x>=-2
=>x^2+4x+4=x-x^2+4-4x và x>=-2
=>2x^2+7x=0 và x>=-2
=>x=0
f: Đặt \(\sqrt[3]{x-1}=a;\sqrt[3]{x-2}=b\)
=>a^3+b^3=2x-3
\(\sqrt[3]{x-1}+\sqrt[3]{x-2}=\sqrt[3]{2x-3}\)
=>a^3+b^3=a^3+b^3+3ba(a+b)
=>ab(a+b)=0
=>x-1=0 hoặc x-2=0 hoặc x-1=-x+2
=>x=1;x=2;x=3/2
Đúng 0
Bình luận (0)