Bài 6: Ôn tập chương Đạo hàm

21:

\(y'=\dfrac{\left(x^2-3x+5\right)'\left(x+2\right)-\left(x+2\right)'\left(x^2-3x+5\right)}{\left(x+2\right)^2}\)

\(=\dfrac{\left(2x-3\right)\left(x+2\right)-\left(x^2-3x+5\right)}{\left(x+2\right)^2}\)

\(=\dfrac{2x^2+4x-3x-6-x^2+3x-5}{\left(x+2\right)^2}=\dfrac{x^2+4x-11}{\left(x+2\right)^2}\)

17:

Khi x<>0 thì \(\lim\limits_{x\rightarrow0}f\left(x\right)=\lim\limits_{x\rightarrow0}\dfrac{1+4x-1}{\sqrt{1+4x}+1}\cdot\dfrac{1}{x}\)

\(=\lim\limits_{x\rightarrow0}\dfrac{4}{\sqrt{1+4x}+1}=\dfrac{4}{1+1}=\dfrac{4}{2}=2\)

=>Chọn B

?

câu nào mà sao bạn trả lời kia-?

..

\(y'=\dfrac{\left(x+\sqrt{1+x^2}\right)'}{2\sqrt{x+\sqrt{1+x^2}}}=\dfrac{1+\dfrac{x}{\sqrt{1+x^2}}}{2\sqrt{x+\sqrt{1+x^2}}}\)

\(\Rightarrow2\sqrt{1+x^2}.y'=\dfrac{2\sqrt{1+x^2}\left(1+\dfrac{x}{\sqrt{1+x^2}}\right)}{2\sqrt{x+\sqrt{1+x^2}}}\)

\(=\dfrac{\sqrt{1+x^2}+x}{\sqrt{x+\sqrt{1+x^2}}}=\sqrt{x+\sqrt{1+x^2}}=y\) (đpcm)

y' > 0 ⇔ \(\dfrac{-1}{2\sqrt{4-x}}+\dfrac{1}{2\sqrt{4+x}}>0\)

⇔ \(\dfrac{1}{2\sqrt{4+x}}>\dfrac{1}{2\sqrt{4-x}}\)

⇔ \(\dfrac{1}{\sqrt{4+x}}>\dfrac{1}{\sqrt{4-x}}\)

⇔ \(\left\{{}\begin{matrix}4-x>0\\4+x>0\\4+x< 4-x\end{matrix}\right.\)

⇔ \(\left\{{}\begin{matrix}4-x>0\\4+x>0\\x< 0\end{matrix}\right.\) ⇔ -4 < x < 0.

Bạn thêm dấu = ở số 0 vào nhé 

Lời giải:

Đạo hàm \(y'=\frac{-1}{2\sqrt{4-x}}+\frac{1}{2\sqrt{4+x}}\)

Đoạn tìm đạo hàm tại $y'\geq 0$ ý bạn là gì nhỉ?

Gọi số hạng có bậc cao nhất của \(f\left(x\right)\) là \(a_n.x^n\)

\(\Rightarrow\) Số hạng bậc cao nhất của \(16f\left(x^2\right)\) là \(16.\left(a_nx^n\right)^2=16a_n^2.x^{2n}\)

Số hạng bậc cao nhất của \(f^2\left(2x\right)\) là: \(\left(a_n.2x^n\right)^2=4a_n^2.x^{2n}\)

Đồng nhất hệ số 2 vế ta được: \(16a_n^2=4a_n^2\Rightarrow a_n=0\)

Hay mọi số hạng chứa x của đa thức đã cho đều có hệ số bằng 0

\(\Rightarrow\) Đa thức đã cho là đa thức hằng

Hay \(f\left(x\right)=k\) với mọi x

Thay vào đề bài: \(16k=k^2\Rightarrow\left[{}\begin{matrix}k=0\\k=16\end{matrix}\right.\)

Vậy có 2 đa thức thỏa mãn: \(\left[{}\begin{matrix}f\left(x\right)\equiv0\\f\left(x\right)\equiv16\end{matrix}\right.\)

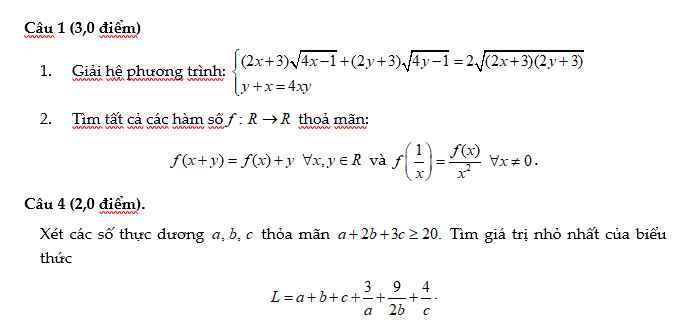
Câu 2:

Cho $x=0$ thì: $f(y)=f(0)+y$ với mọi $y\in\mathbb{R}$

Thay vô điều kiện số 2:

$f(0)+\frac{1}{y}=\frac{f(0)+y}{y^2}, \forall y\neq 0$

$\Rightarrow f(0)y^2+y=f(0)+y, \forall y\neq 0$

$\Leftrightarrow f(0)y^2=f(0), \forall y\neq 0$

$\Rightarrow f(0)=0$

Khi đó: $f(y)=f(0)+y=y, \forall y\in\mathbb{R}$

\(y'=-\dfrac{\left(32-3x^3\right)'}{\left(32-3x^3\right)^2}=\dfrac{9x^2}{\left(32-3x^3\right)^2}\)

a) `f^((n)) (x) = ((x+10)^6)^((n)) = 0 (n>6)`

b) `f^((n)) (x) = (cosx)^((n)) = cos(x+ (nπ)/2)`

c) `f^((n)) (x) = (sinx)^((n)) = sin(x + (nπ)/2)`