Bài 4: Hàm số mũ. Hàm số logarit
Nội dung lý thuyết
Các phiên bản khácI. HÀM SỐ MŨ
1. Định nghĩa
Cho số thực dương \(a\) khác 1.
Hàm số \(y=a^x\) được gọi là hàm số mũ cơ số \(a\).
Ví dụ: \(y=\left(\sqrt{3}\right)^x\) là hàm số mũ cơ số \(\sqrt{3}\).
2. Đạo hàm của hàm số mũ
Ta thừa nhận công thức: \(\lim\limits_{t\rightarrow0}\dfrac{e^t-1}{t}=1\)
Định lí 1:
Hàm số \(y=e^x\) có đạo hàm tại mọi \(x\) và
\(\left(e^x\right)'=e^x\).
Chú ý: Công thức đạo hàm của hàm hợp đối với hàm số \(e^u\left(u=u\left(x\right)\right)\) là \(\left(e^u\right)'=u'.e^u\).
Định lí 2:
Hàm số \(y=a^x\left(a>0,a\ne1\right)\) có đạo hàm tại mọi \(x\) và
\(\left(a^x\right)'=a^x\ln a\).
Chú ý: Đối với hàm hợp \(a^{u\left(x\right)}\) ta có: \(\left(a^{u\left(x\right)}\right)'=a^u\ln a.u'\).
Ví dụ 1: Tính đạo hàm của hàm số \(y=8^{x^2+x+1}\).
Giải:
Ta có: \(y'=\left(8^{x^2+x+1}\right)'=8^{x^2+x+1}.\ln8.\left(x^2+x+1\right)'=8^{x^2+x+1}\left(2x+1\right)\ln8\).
3. Khảo sát hàm số mũ \(y=a^x\left(a>0,a\ne1\right)\)
| \(y=a^x,a>1\) | \(y=a^x,0< a< 1\) |
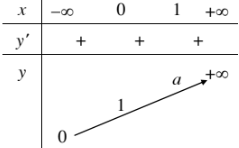
1. Tập xác định: \(R\). 2. Sự biến thiên: \(y'=a^x\ln a>0,\forall x\) Giới hạn đặc biệt: \(\lim\limits_{x\rightarrow-\infty}a^x=0,\lim\limits_{x\rightarrow+\infty}a^x=+\infty\) Tiệm cận: Trục Ox là tiệm cận ngang 3. Bảng biến thiên:
4. Đồ thị:
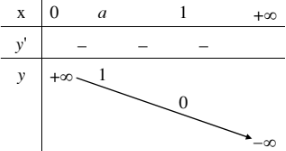
Đồ thị đi qua điểm \(\left(0;1\right)\) và \(\left(1;a\right)\), nằm phía trên trục hoành. | 1. Tập xác định: \(R\). 2. Sự biến thiên: \(y'=a^x\ln a< 0,\forall x\) Giới hạn đặc biệt: \(\lim\limits_{x\rightarrow-\infty}a^x=+\infty,\lim\limits_{x\rightarrow+\infty}a^x=0\) Tiệm cận: Trục Ox là tiệm cận ngang 3. Bảng biến thiên:
4. Đồ thị:
Đồ thị đi qua điểm \(\left(0;1\right)\) và \(\left(1;a\right)\), nằm phía trên trục hoành. |
@29548@
II. HÀM SỐ LÔGARIT
1. Định nghĩa
Cho số thực dương \(a\) khác 1.
Hàm số \(y=\log_ax\) được gọi là hàm số lôgarit cơ số \(a\).
Ví dụ: Các hàm số \(y=\log_3x,y=\log_{\dfrac{1}{4}}x,y=\ln x,y=\log x\) là các hàm số lôgarit với cơ số lần lượt là \(3,\dfrac{1}{4},e,10\).
2. Đạo hàm của hàm số lôgarit
Định lí 3:
Hàm số \(y=\log_ax\) \(\left(a>0,a\ne1\right)\) có đạo hàm tại mọi \(x>0\) và
\(\left(\log_ax\right)'=\dfrac{1}{x\ln a}\).
Đặc biệt: \(\left(\ln x\right)'=\dfrac{1}{x}\).
Chú ý: Đối với hàm hợp \(\log_au\left(x\right)\) ta có: \(\left(\log_au\left(x\right)\right)'=\dfrac{u'}{u\ln a}\).
Ví dụ 2. Tính đạo hàm của hàm số \(y=\log_2\left(2x+1\right)\).
Giải:
Ta có \(y'=\left(\log_2\left(2x+1\right)\right)'=\dfrac{\left(2x+1\right)'}{\left(2x+1\right)\ln2}=\dfrac{2}{\left(2x+1\right)\ln2}\).
@54815@
3. Khảo sát hàm số \(y=\log_ax\) \(\left(a>0,a\ne1\right)\)
| \(y=\log_ax\), \(a>1\) | \(y=\log_ax\), \(0< a< 1\) |
1. Tập xác định: \(\left(0;+\infty\right)\). 2. Sự biến thiên: \(y'=\dfrac{1}{x\ln a}>0,\forall x>0\) Giới hạn đặc biệt: \(\lim\limits_{x\rightarrow0^+}\log_ax=-\infty\) ; \(\lim\limits_{x\rightarrow+\infty}\log_ax=+\infty\) Tiệm cận: Trục Oy là tiệm cận đứng 3. Bảng biến thiên:
4. Đồ thị:
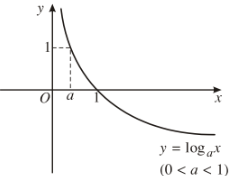
Đồ thị đi qua các điểm \(\left(1;0\right)\) và \(\left(a;1\right)\), nằm phía bên phải trục tung. | 1. Tập xác định: \(\left(0;+\infty\right)\). 2. Sự biến thiên: \(y'=\dfrac{1}{x\ln a}< 0,\forall x>0\) Giới hạn đặc biệt: \(\lim\limits_{x\rightarrow0^+}\log_ax=+\infty\) ; \(\lim\limits_{x\rightarrow+\infty}\log_ax=-\infty\) Tiệm cận: Trục Oy là tiệm cận đứng 3. Bảng biến thiên:
4. Đồ thị:
Đồ thị đi qua các điểm \(\left(1;0\right)\) và \(\left(a;1\right)\), nằm phía bên phải trục tung. |
Nhận xét: Đồ thị của các hàm số \(y=a^x\) và \(y=\log_ax\) \(\left(a>0,a\ne1\right)\) đối xứng với nhau qua đường thẳng \(y=x\).
@42104@
Danh sách các phiên bản khác của bài học này. Xem hướng dẫn
| Nguyễn Phương Mai đã đóng góp một phiên bản khác cho bài học này (12 tháng 2 2022 lúc 15:25) | 0 lượt thích |