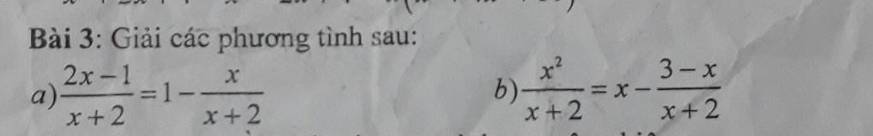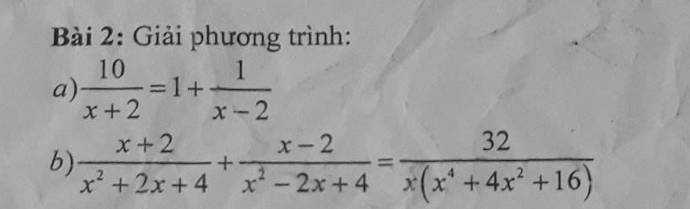Bài 5: Phương trình chứa ẩn ở mẫu

\(\dfrac{3x+2}{x-1}=3\left(x\ne1\right)\)

suy ra

`3x+2=3(x-1)`

`<=>3x+2=3x-3`

`<=> 3x-3x=-3-2`

`<=> 0x=-5` (vô lí vì 0x=0 với mọi x)

\(\dfrac{3x+2}{x-1}=3\) (ĐK: x ≠ 1)

\(\Leftrightarrow3x+2=3\left(x-1\right)\)

\(\Leftrightarrow3x+2=3x-3\)

\(\Leftrightarrow3x-3x=-3-2\)

\(\Leftrightarrow0x=-5\) (Vô lí)

Vậy \(S=\varnothing\).

\(\dfrac{3x+2}{x-1}=3\) \(\left(dkxd:x\ne1\right)\)

\(\Leftrightarrow3x+2=3\left(x-1\right)\)

\(\Leftrightarrow3x+2=3x-3\)

\(\Leftrightarrow3x-3x=-3-2\)

\(\Leftrightarrow0=-5\left(VL\right)\)

Vậy \(S=\varnothing\)

\(\dfrac{3}{x+5}=\dfrac{4}{x-2}\left(x\ne-5;x\ne2\right)\)

suy ra

`3(x-2)=4(x+5)`

`<=>3x-6=4x+20`

`<=> 3x-4x=20+6`

`<=> -x=26`

`<=> x=-26(tm)`

\(\dfrac{3}{x+5}=\dfrac{4}{x-2}\left(ĐKXĐ:x\ne-5;x\ne2\right)\)

\(\Leftrightarrow3\left(x-2\right)=4\left(x+5\right)\)

\(\Leftrightarrow3x-6=4x+20\)

\(\Leftrightarrow3x-4x=20+6\)

\(\Leftrightarrow-x=26\)

\(\Leftrightarrow x=-26\left(tm\right)\)

`(x-2)/(x+1)=2` ĐK `x≠-1`

`<=> (x-2)/(x+1) = (2(x+1))/(x+1)`

`=>x-2 = 2(x+1)`

`<=>x-2=2x+2`

`<=>x-2x=2+2`

`<=> -x=4`

`<=>x=-4(TM)`

=>2x+2=x-2

=>x=-4

\(\dfrac{x-2}{x+1}=2\left(x\ne-1\right)\)

suy ra

`x-2=2(x+1)`

`<=>x-2=2x+2`

`<=> x-2x=2+2`

`<=> -x=4`

`<=> x=-4(tm)`

a: x^2+2x+3=(x+1)^2+2>0

x^2-x+1=(x-1/2)^2+3/4>0

=>PTVN

b: =>x(x-2)+4(x+2)=4

=>x^2-2x+4x+8=4

=>x^2+2x+4=0

=>(x+1)^2+3=0(loại)

\(a,\dfrac{2x-1}{x+2}=1-\dfrac{x}{x+2}\left(dkxd:x\ne-2\right)\)

\(\Leftrightarrow2x-1-x-2+x=0\)

\(\Leftrightarrow2x=3\)

\(\Leftrightarrow x=\dfrac{3}{2}\left(n\right)\)

\(b,\dfrac{x^2}{x+2}=x-\dfrac{3-x}{x+2}\left(dkxd:x\ne-2\right)\)

\(\Leftrightarrow x^2-x\left(x+2\right)+3-x=0\)

\(\Leftrightarrow x^2-x^2-2x+3-x=0\)

\(\Leftrightarrow-3x=-3\)

\(\Leftrightarrow x=1\left(n\right)\)

a)

\(\dfrac{2x-1}{x+2}=1-\dfrac{x}{x+2}\left(x\ne-2\right)\)

suy ra:

`2x-1=x+2-x`

`<=> 2x-x+x=2+1`

`<=> 2x=3`

`<=> x=3/2 (tm)`

b)

\(\dfrac{x}{x+2}=x-\dfrac{3-x}{x+2}\left(x\ne-2\right)\)

suy ra:

`x=x^2 +2x-3+x`

`<=> x^2 +2x-x+x-3=0`

`<=> x^2 +2x-3=0`

`<=> x^2 +3x-x-3=0`

`<=> x(x+3)-(x+3)=0`

`<=> (x+3)(x-1)=0`

\(< =>\left[{}\begin{matrix}x+3=0\\x-1=0\end{matrix}\right.\\ < =>\left[{}\begin{matrix}x=-3\left(tm\right)\\x=1\left(tm\right)\end{matrix}\right.\)

a: =>2x-1=x+2-x

=>2x-1=2

=>2x=3

=>x=3/2

b: =>x^2=x(x+2)-3+x

=>x^2=x^2+2x-3+x

=>3x-3=0

=>x=1

a: =>10(x-2)=x^2-4+x+2

=>x^2+x-2=10x-20

=>x^2-9x+18=0

=>(x-3)(x-6)=0

=>x=3 hoặc x=6

b: \(\Leftrightarrow\dfrac{\left(x+2\right)\cdot\left(x^2-2x+4\right)+\left(x-2\right)\left(x^2+2x+4\right)}{\left(x^2+2x+4\right)\left(x^2-2x+4\right)}=\dfrac{32}{x\left(x^2+2x+4\right)\left(x^2-2x+4\right)}\)

\(\Leftrightarrow2x^3\cdot x=32\)

=>2x^4=32

=>x=2 hoặc x=-2

a) ĐKXĐ: \(x\ne-2\)

                \(x\ne2\)

\(\dfrac{10\left(x-2\right)}{\left(x+2\right)\left(x-2\right)}=\dfrac{\left(x+2\right)\left(x-2\right)}{\left(x+2\right)\left(x-2\right)}+\dfrac{x+2}{\left(x+2\right)\left(x-2\right)}\)

Suy ra:  \(10x-20=x^2-2x+2x-4+x+2\)

    <=>   \(10x-20-x^2+2x-2x+4-x-2=0\)

    <=>   \(-x^2+9x-18=0\)

    <=>   \(0=x^2-9x+18\)

    <=>    \(0=\left(x-9\right)^2\)

    <=>    \(x-9=0\)

    <=>    \(x=9\)

Vậy \(S=\left\{9\right\}\)

j: \(\Leftrightarrow\left(x-1\right)\left(x-2\right)-x\left(x+2\right)=-5x+2\)

=>x^2-3x+2-x^2-2x=-5x+2

=>-5x+2=-5x+2

=>0x=0(luôn đúng)

k: =>(x-2)^2-3(x+2)=2x-22

=>x^2-4x+4-3x-6=2x-22

=>x^2-7x-2-2x+22=0

=>x^2-9x+20=0

=>x=4 hoặc x=5

\(\dfrac{9}{x+3}=\dfrac{8}{x-1}\) (ĐK: x ≠ 1;-3)

\(\Leftrightarrow9\left(x-1\right)=8\left(x+3\right)\)

\(\Leftrightarrow9x-9=8x+24\)

\(\Leftrightarrow9x-8x=24+9\)

\(\Leftrightarrow x=33\) (TMĐK)

\(\dfrac{5x-2}{x+1}=4\) ĐK : \(x\ne-1\)

\(\Leftrightarrow\dfrac{5x-2}{x+1}=\dfrac{4\left(x+1\right)}{x+1}\)

`=>5x-2=4(x+1)`

`<=> 5x-2=4x+4`

`<=>5x-4x=4+2`

`<=>x=6(TM)`