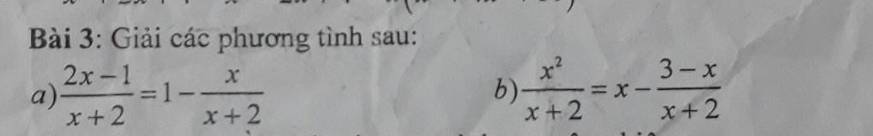\(a,\dfrac{2x-1}{x+2}=1-\dfrac{x}{x+2}\left(dkxd:x\ne-2\right)\)
\(\Leftrightarrow2x-1-x-2+x=0\)
\(\Leftrightarrow2x=3\)
\(\Leftrightarrow x=\dfrac{3}{2}\left(n\right)\)
\(b,\dfrac{x^2}{x+2}=x-\dfrac{3-x}{x+2}\left(dkxd:x\ne-2\right)\)
\(\Leftrightarrow x^2-x\left(x+2\right)+3-x=0\)
\(\Leftrightarrow x^2-x^2-2x+3-x=0\)
\(\Leftrightarrow-3x=-3\)
\(\Leftrightarrow x=1\left(n\right)\)
a)
\(\dfrac{2x-1}{x+2}=1-\dfrac{x}{x+2}\left(x\ne-2\right)\)
suy ra:
`2x-1=x+2-x`
`<=> 2x-x+x=2+1`
`<=> 2x=3`
`<=> x=3/2 (tm)`
b)
\(\dfrac{x}{x+2}=x-\dfrac{3-x}{x+2}\left(x\ne-2\right)\)
suy ra:
`x=x^2 +2x-3+x`
`<=> x^2 +2x-x+x-3=0`
`<=> x^2 +2x-3=0`
`<=> x^2 +3x-x-3=0`
`<=> x(x+3)-(x+3)=0`
`<=> (x+3)(x-1)=0`
\(< =>\left[{}\begin{matrix}x+3=0\\x-1=0\end{matrix}\right.\\ < =>\left[{}\begin{matrix}x=-3\left(tm\right)\\x=1\left(tm\right)\end{matrix}\right.\)
a: =>2x-1=x+2-x
=>2x-1=2
=>2x=3
=>x=3/2
b: =>x^2=x(x+2)-3+x
=>x^2=x^2+2x-3+x
=>3x-3=0
=>x=1