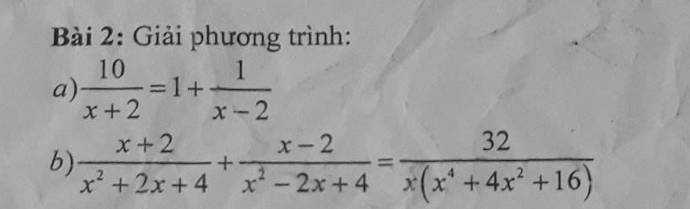a: =>10(x-2)=x^2-4+x+2
=>x^2+x-2=10x-20
=>x^2-9x+18=0
=>(x-3)(x-6)=0
=>x=3 hoặc x=6
b: \(\Leftrightarrow\dfrac{\left(x+2\right)\cdot\left(x^2-2x+4\right)+\left(x-2\right)\left(x^2+2x+4\right)}{\left(x^2+2x+4\right)\left(x^2-2x+4\right)}=\dfrac{32}{x\left(x^2+2x+4\right)\left(x^2-2x+4\right)}\)
\(\Leftrightarrow2x^3\cdot x=32\)
=>2x^4=32
=>x=2 hoặc x=-2
a) ĐKXĐ: \(x\ne-2\)
\(x\ne2\)
\(\dfrac{10\left(x-2\right)}{\left(x+2\right)\left(x-2\right)}=\dfrac{\left(x+2\right)\left(x-2\right)}{\left(x+2\right)\left(x-2\right)}+\dfrac{x+2}{\left(x+2\right)\left(x-2\right)}\)
Suy ra: \(10x-20=x^2-2x+2x-4+x+2\)
<=> \(10x-20-x^2+2x-2x+4-x-2=0\)
<=> \(-x^2+9x-18=0\)
<=> \(0=x^2-9x+18\)
<=> \(0=\left(x-9\right)^2\)
<=> \(x-9=0\)
<=> \(x=9\)
Vậy \(S=\left\{9\right\}\)