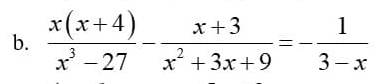 giúp với ạ
giúp với ạ
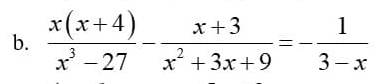 giúp với ạ
giúp với ạ
\(\dfrac{x\left(x+4\right)}{x^3-27}-\dfrac{x+3}{x^2+3x+9}=-\dfrac{1}{3-x}\left(dkxd:x\ne3\right)\)
\(\Leftrightarrow\dfrac{x^2+4x}{\left(x-3\right)\left(x^2+3x+9\right)}-\dfrac{x+3}{x^2+3x+9}+\dfrac{1}{3-x}=0\)
\(\Leftrightarrow\dfrac{x^2+4x}{\left(x-3\right)\left(x^2+3x+9\right)}-\dfrac{x+3}{x^2+3x+9}-\dfrac{1}{x-3}=0\)
\(\Leftrightarrow\dfrac{x^2+4x-\left(x+3\right)\left(x-3\right)-\left(x^2+3x+9\right)}{\left(x-3\right)\left(x^2+3x+9\right)}=0\)
\(\Leftrightarrow x^2+4x-\left(x^2-9\right)-\left(x^2+3x+9\right)=0\)
\(\Leftrightarrow x^2+4x-x^2+9-x^2-3x-9=0\)
\(\Leftrightarrow-x^2+x=0\)
\(\Leftrightarrow-x\left(x-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=1\end{matrix}\right.\) \(\left(tmdk\right)\)
Vậy \(S=\left\{0;1\right\}\)
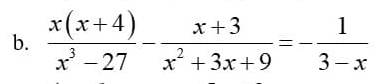 giúp mình với ạ
giúp mình với ạ
Lời giải:
ĐKXĐ: $x\neq 3$
PT $\Leftrightarrow \frac{x(x+4)}{x^3-27}=\frac{x+3}{x^2+3x+9}-\frac{1}{3-x}=\frac{x+3}{x^2+3x+9}+\frac{1}{x-3}=\frac{(x+3)(x-3)+(x^2+3x+9)}{(x^2+3x+9)(x-3)}=\frac{2x^2+3x}{x^2-27}$
$\Rightarrow x(x+4)=2x^2+3x$
$\Leftrightarrow x^2-x=0$
$\Leftrightarrow x(x-1)=0$
$\Rightarrow x=0$ hoặc $x=1$ (tm)
Câu1: Trong các phương trình sau, phương trình nào tương đương với phương trình x=2
A x²-4=0
B.2x-4=0
C.x(x-2)=0
D.x=-2
Câu2 : Giả sử hằng ngày bạn Tiến dành x giờ để tập chạy với vận tốc trung bình là 10km/h. Biểu thức nào sau đây biểu thị quãng đường Tiến chạy được trong x giờ là A.10+x
B.10.x
C.x/10
D.10/x
1 - B
\(2x-4=0\)
\(\Leftrightarrow2x=4\)
\(\Leftrightarrow x=2\)
2 - B
| QĐ | VT | TG |
| \(10x\) | \(10\) | \(x\) |
a. 3x-1=-17
b. 40-(3x-8)=3(3-5x)
c. x/2(x-2) + x/2x+2 = 2x/(x+1)(x-2) e cảm ơn mng nhìuu
a) 3x-1=-17
<=>3x=-16
<=>x=-16/3
Vậy...
b) 40-(3x-8)=3(3-5x)
<=>40-3x+8=9-15x
<=>12x = -39
<=> x = -13/4
Vậy ...
c) x/2(x-2) + x/2x+2 = 2x/(x+1)(x-2)
<=> x/2(x-2) + x/2(x+1) = 2x/(x+1)(x-2)
<=> x(x+1)/2(x-2)(x+1) + x(x-2)/2(x+1)(x-2) = 4x/2(x+1)(x-2)
=>x(x+1) + x(x-2) = 4x
<=> x2 + x + x2 -2x = 4x
<=> 2x^2 -5x = 0
<=> x(2x-5) = 0
<=>x=0 hoặc 2x-5=0
<=>x=0 <=>x=5/2
Vậy...
(Nhớ tick mik nha)
a: =>3x=-16
=>x=-16/3
b: =>40-3x+8=9-15x
=>-3x+48=9-15x
=>12x=-39
=>x=-13/4
c: =>x(x+1)+x(x-2)=4x
=>x^2+x+x^2-2x-4x=0
=>2x^2-5x=0
=>x=0 hoặc x=5/2
Cho mình hỏi là trong pt: x+2/x-2 - x-2/x+2= -4/(x+2)(x-2)thì khi khử mẫu rồi, có đổi -4 thành 4 ko ạ
giải giùm mình bài này với (x-2)(2x+3)-3x=11
`(x-2)(2x+3)-3x=11`
`<=> 2x^2 - 4x + 3x - 6 - 3x -11 = 0`
`<=> 2x^2 - 4x - 17 = 0`
`<=> 2x^2 - 4x + 2 - 19 = 0`
`<=> 2 (x-1)^2 = 19`
`<=> (x-1)^2 = 19/2`
`<=> x - 1 = sqrt{19/2}` hoặc `x - 1 = -sqrt{19/2}`
`<=> x = sqrt{19/2} +1` hoặc `x = -sqrt{19/2} + 1`
`<=> x = (2 + sqrt{38})/2` hoặc `x = (2 - sqrt{38})/2`
1/(x-3)+2=5/(x-1)+x
1/(x-3)+2=5/(x-1)+x
1:x-1:3=5:x-5:1+x
1:x-1/3=5:x-5+x
1x-3+2=6x-1
<=>-5x=0
<=>x=0
#YH
x-3/x+1=x²/x²-1
\(\dfrac{x-3}{x+1}=\dfrac{x^2}{x^2-1}\left(x\ne-1;x\ne1\right)\\ < =>\dfrac{\left(x-3\right)\left(x-1\right)}{\left(x+1\right)\left(x-1\right)}=\dfrac{x^2}{\left(x-1\right)\left(x+1\right)}\)
suy ra
`(x-3)(x-1)=x^2`
`<=> x^2 -x-3x+3=x^2`
`<=> x^2 -x^2 -x-3x+3=0`
`<=>-4x=-3`
`<=>x=3/4(tm)`
\(\dfrac{x-3}{x+1}=\dfrac{x^2}{x^2-1}\)
\(ĐKXĐ:x+1\ne0\)
\(x\ne-1\)
\(x-1\ne0\)
\(x\ne1\)
\(\Leftrightarrow\left(x-3\right)\left(x-1\right)=x^2\)
\(\Leftrightarrow x^2-4x+3-x^2=0\)
\(\Leftrightarrow-4x+3=0\)
\(\Leftrightarrow-4x=-3\)
\(\Leftrightarrow x=\dfrac{3}{4}\)(nhận)
\(S=\left\{\dfrac{3}{4}\right\}\)
Giải phương trình
\(\dfrac{x-3}{x-2}\)+\(\dfrac{x-2}{x-4}\)= -1
ĐKXĐ: \(x\ne\left\{2;4\right\}\)
\(\dfrac{x-3}{x-2}+\dfrac{x-2}{x-4}=-1\)
\(\Leftrightarrow\dfrac{\left(x-3\right)\left(x-4\right)}{\left(x-2\right)\left(x-4\right)}+\dfrac{\left(x-2\right)^2}{\left(x-2\right)\left(x-4\right)}=-\dfrac{\left(x-2\right)\left(x-4\right)}{\left(x-2\right)\left(x-4\right)}\)
\(\Rightarrow\left(x-3\right)\left(x-4\right)+\left(x-2\right)^2=-\left(x-2\right)\left(x-4\right)\)
\(\Leftrightarrow x^2-7x+12+x^2-4x+4=-x^2+6x-8\)
\(\Leftrightarrow3x^2-17x+24=0\)
\(\Leftrightarrow3x^2-9x-8x+24=0\)
\(\Leftrightarrow3x\left(x-3\right)-8\left(x-3\right)=0\)
\(\Leftrightarrow\left(x-3\right)\left(3x-8\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=3\\x=\dfrac{8}{3}\end{matrix}\right.\) (thỏa mãn)
giải phương trình:
\(\dfrac{4x}{x^2+4x+3}\)-1 = 6 \(\left(\dfrac{1}{x+3}-\dfrac{1}{2x+2}\right)\)
\(\dfrac{4x}{x^2+4x+3}-1=6\left(\dfrac{1}{x+3}-\dfrac{1}{2x+2}\right)\left(x\ne-3;x\ne-1\right)\\ < =>\dfrac{4x}{x^2+4x+4-1}-1=\dfrac{6}{x+3}-\dfrac{6}{2x+2}\\ < =>\dfrac{4x}{\left(x+2\right)^2-1}-1=\dfrac{6}{x+3}-\dfrac{6}{2\left(x+1\right)}\\ < =>\dfrac{4x}{\left(x+1\right)\left(x+3\right)}-1=\dfrac{6}{x+3}-\dfrac{3}{x+1}\)
suy ra:
`4x-(x+1)(x+3)=6(x+1)-3(x+3)`
\(< =>4x-\left(x^2+3x+x+3\right)=6x+6-3x-9\)
\(< =>4x-x^2-4x-3=6x+6-3x-9\)
\(< =>-x^2+4x-4x-6x+3x-3-6+9=0\)
\(< =>-x^2-3x=0\\ < =>x^2+3x=0\\ < =>x\left(x+3\right)=0\\ < =>\left[{}\begin{matrix}x=0\\x+3=0\end{matrix}\right.\\ < =>\left[{}\begin{matrix}x=0\left(tm\right)\\x=-3\left(ktmđk\right)\end{matrix}\right.\)
vậy pt có tập nghiệm S={0}