\(\dfrac{x\left(x+4\right)}{x^3-27}-\dfrac{x+3}{x^2+3x+9}=-\dfrac{1}{3-x}\left(dkxd:x\ne3\right)\)
\(\Leftrightarrow\dfrac{x^2+4x}{\left(x-3\right)\left(x^2+3x+9\right)}-\dfrac{x+3}{x^2+3x+9}+\dfrac{1}{3-x}=0\)
\(\Leftrightarrow\dfrac{x^2+4x}{\left(x-3\right)\left(x^2+3x+9\right)}-\dfrac{x+3}{x^2+3x+9}-\dfrac{1}{x-3}=0\)
\(\Leftrightarrow\dfrac{x^2+4x-\left(x+3\right)\left(x-3\right)-\left(x^2+3x+9\right)}{\left(x-3\right)\left(x^2+3x+9\right)}=0\)
\(\Leftrightarrow x^2+4x-\left(x^2-9\right)-\left(x^2+3x+9\right)=0\)
\(\Leftrightarrow x^2+4x-x^2+9-x^2-3x-9=0\)
\(\Leftrightarrow-x^2+x=0\)
\(\Leftrightarrow-x\left(x-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=1\end{matrix}\right.\) \(\left(tmdk\right)\)
Vậy \(S=\left\{0;1\right\}\)
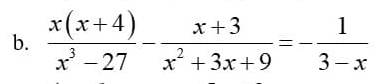 giúp với ạ
giúp với ạ

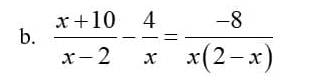 giúp mình với ạ
giúp mình với ạ