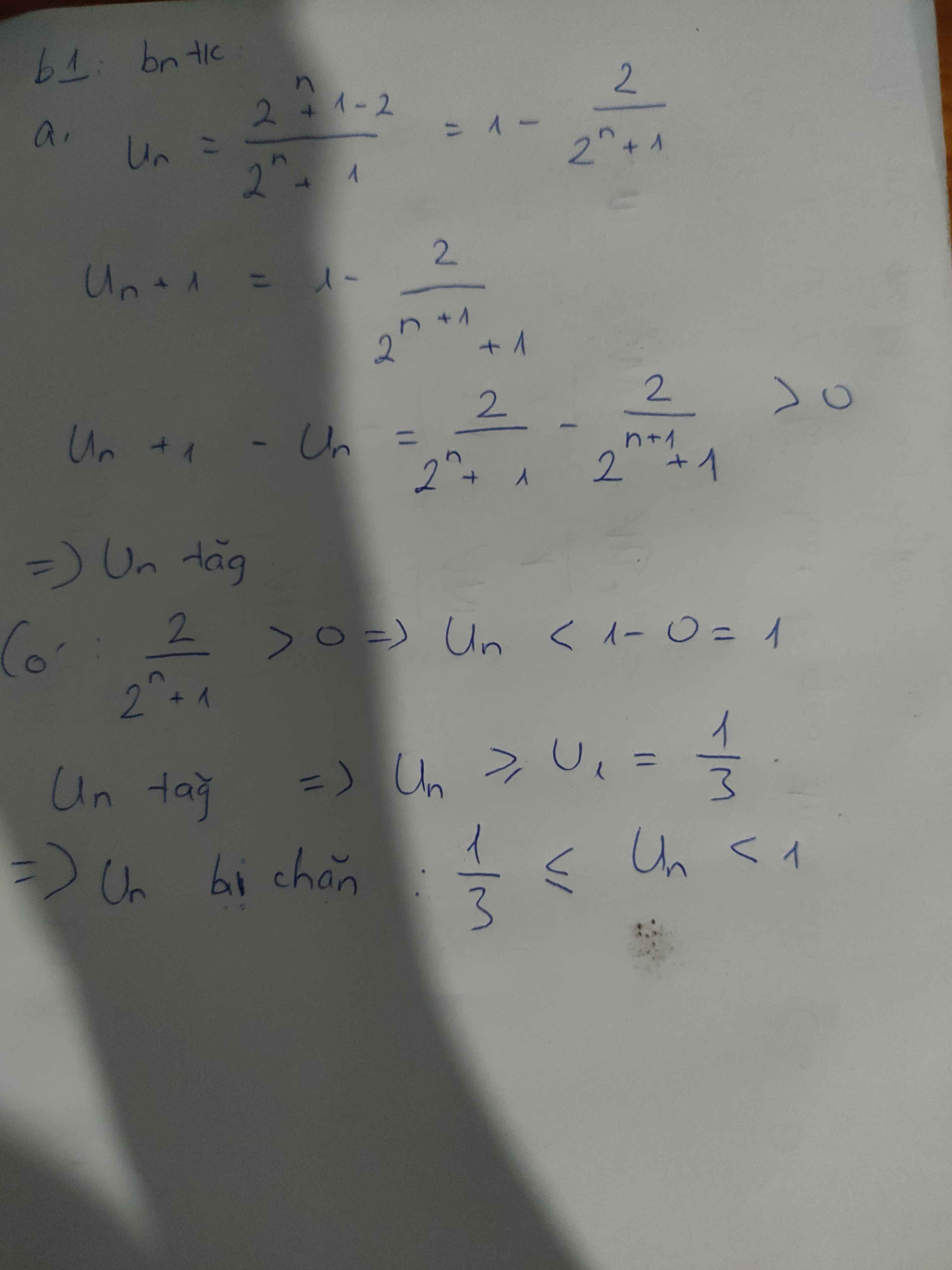Câu 1,2,3 nhaa em cảm ơn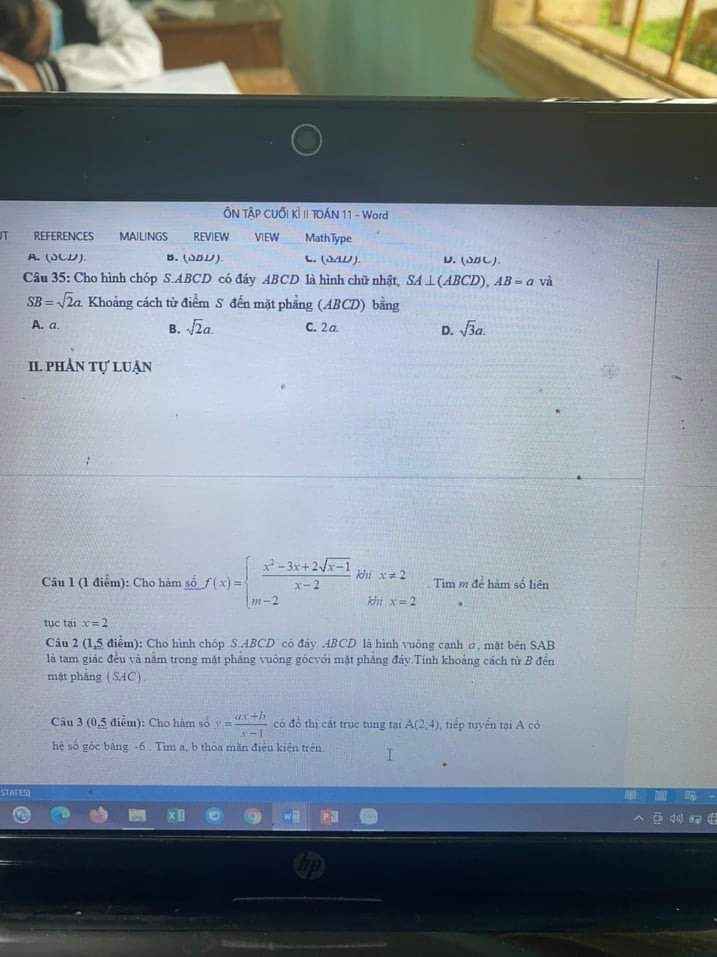
Bài 5: Ôn tập chương Dãy số. Cấp số cộng và cấp số nhân.
1.
\(\lim\limits_{x\rightarrow2}f\left(x\right)=\lim\limits_{x\rightarrow2}\dfrac{x^2-3x+2\sqrt{x-1}}{x-2}\)
\(=\lim\limits_{x\rightarrow2}\dfrac{x^2-3x+2+2\left(\sqrt{x-1}-1\right)}{x-2}\)
\(=\lim\limits_{x\rightarrow2}\dfrac{\left(x-1\right)\left(x-2\right)+\dfrac{2\left(x-2\right)}{\sqrt{x-1}+1}}{x-2}\)
\(=\lim\limits_{x\rightarrow2}\left(x-1+\dfrac{2}{\sqrt{x-1}+1}\right)=2\)
\(f\left(2\right)=m-2\)
Hàm liên tục tại \(x=2\) khi \(\lim\limits_{x\rightarrow2}f\left(x\right)=f\left(2\right)\)
\(\Leftrightarrow m-2=2\Rightarrow m=4\)
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
Câu 4 ạ
\(x^2+y^2+xy+2-3x-3y=0\)
\(\Leftrightarrow\left(x+\dfrac{y}{2}-\dfrac{3}{2}\right)^2+\dfrac{3}{4}\left(y-1\right)^2=1\)
Đặt \(\left\{{}\begin{matrix}x+\dfrac{y}{2}-\dfrac{3}{2}=sina\\\dfrac{\sqrt{3}}{2}\left(y-1\right)=cosa\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=sina-\dfrac{y-3}{2}\\y=\dfrac{2}{\sqrt{3}}cosa+1\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=sina-\dfrac{1}{\sqrt{3}}cosa+1\\y=\dfrac{2}{\sqrt{3}}cosa+1\end{matrix}\right.\)
\(\Rightarrow P=\dfrac{3sina+\dfrac{1}{\sqrt{3}}cosa+6}{sina+\dfrac{1}{\sqrt{3}}cosa+8}\)
\(\Rightarrow P.sina-\dfrac{P}{\sqrt{3}}cosa+8P=3sina+\dfrac{1}{\sqrt{3}}cosa+6\)
\(\Rightarrow\left(P-3\right)sina-\left(\dfrac{P+1}{\sqrt{3}}\right)cosa=6-8P\)
Theo điều kiện có nghiệm của pt lượng giác bậc nhất:
\(\left(P-3\right)^2+\left(\dfrac{P+1}{\sqrt{3}}\right)^3\ge\left(6-8P\right)^2\)
\(\Leftrightarrow47P^2-67P+20\le0\)
\(\Rightarrow\dfrac{20}{47}\le P\le1\)
Đúng 1
Bình luận (0)
giúp mình với!!
4. Cho lim\(\dfrac{an^3+n^2+1}{n^2+n}=1\)
Tìm a
A. a=1 B. a=2 C.a=4 D. a=0
Cho mình xin đáp án và lời giải chi tiết với ạ1. cho cấp số nhân có u12, q2. Tính SnA. Sn2nB. Sn2n-1C.Sn2n-2D. Sn2n+1-22. Cho cấp số cộng thỏa mãnleft{{}begin{matrix}u_2+u_512u_4+u_822end{matrix}right.. Tính SnA. Snn2 B. Sn2n C.Sn2n-13. cho cấp số nhân thỏa mãnleft{{}begin{matrix}u_1+u_24u_4+u_128end{matrix}right. Tìm qA.. q2 B.q3 C.q4 D.q5
Đọc tiếp
Cho mình xin đáp án và lời giải chi tiết với ạ
1. cho cấp số nhân có u1=2, q=2. Tính Sn
A. Sn=2n
B. Sn=2n-1
C.Sn=2n-2
D. Sn=2n+1-2
2. Cho cấp số cộng thỏa mãn\(\left\{{}\begin{matrix}u_2+u_5=12\\u_4+u_8=22\end{matrix}\right.\). Tính Sn
A. Sn=n2 B. Sn=2n C.Sn=2n-1
3. cho cấp số nhân thỏa mãn\(\left\{{}\begin{matrix}u_1+u_2=4\\u_4+u_1=28\end{matrix}\right.\)
Tìm q
A.. q=2 B.q=3 C.q=4 D.q=5
1. Áp dụng công thức tổng cấp số nhân:
\(S_n=u_1.\dfrac{q^n-1}{q-1}=2.\dfrac{2^n-1}{2-1}=2.\left(2^n-1\right)=2^{n+1}-2\)
2. \(\left\{{}\begin{matrix}u_2+u_5=12\\u_4+u_8=22\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}\left(u_1+d\right)+\left(u_1+4d\right)=12\\\left(u_1+3d\right)+\left(u_1+7d\right)=22\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}2u_1+5d=12\\2u_1+10d=22\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}u_1=1\\d=2\end{matrix}\right.\)
\(\Rightarrow u_n=u_1+\left(n-1\right)d=1+\left(n-1\right)2=2n-1\)
\(\Rightarrow S_n=\dfrac{n\left(u_1+u_n\right)}{2}=\dfrac{n\left(1+2n-1\right)}{2}=n^2\)
3. \(\left\{{}\begin{matrix}u_1+u_2=4\\u_4+u_1=28\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}u_1+u_1q=4\\u_1q^3+u_1=28\end{matrix}\right.\)
\(\Rightarrow\dfrac{q^3+1}{q+1}=\dfrac{28}{4}\Rightarrow q^2-q+1=7\)
\(\Rightarrow q^2-q-6=0\Rightarrow\left[{}\begin{matrix}q=3\\q=-2\end{matrix}\right.\)
Đúng 1
Bình luận (0)
Mọi người ơi cho em hỏi ngoài lề một chút ạ. E có thi gk trên azota theo đường link của cô giáo gửi, vậy trong lúc đó e vừa làm bài vừa call trên cùng một thiết bị thì có bị hệ thống azota ghi lại đoạn hội thoại đó không ạ?. Mong mn giải đáp giúp e ạ😔😔

giúp em với em cảm ơn nhiềuuuuu
Do n lẻ, đặt \(n=2m+1\)
\(\Rightarrow S=C_{2m+1}^1+C_{2m+1}^2+...+C_{2m+1}^m\)
Áp dụng đẳng thức: \(C_n^k=C_n^{n-k}\)
\(\Rightarrow S=C_{2m+1}^{2m}+C_{2m+1}^{2m-1}+...+C_{2m+1}^{m+1}\)
\(\Rightarrow2S=S+S=C_{2m+1}^1+C_{2m+1}^2+...+C_{2m+1}^{2m}\)
\(=C_{2m+1}^0+C_{2m+1}^1+...+C_{2m+1}^{2m+1}-\left(C_{2m+1}^0+C_{2m+1}^{2m+1}\right)\)
\(=2^{2m+1}-2\)
\(\Rightarrow S=2^{2m}-1\) luôn lẻ (đpcm)
Đúng 2
Bình luận (0)
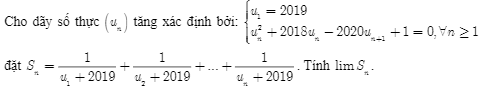
giúp em với ạ
Do \(\left(u_n\right)\) là dãy tăng nên \(u_n\ge2018,\forall n\ge1\)
Ta có : \(u^2_n+2018u_n-2020u_{n+1}=0\) \(\Leftrightarrow u_{n+1}=\dfrac{u^2_n+2018u_n+1}{2020}\)
\(\Leftrightarrow u_{n+1}-1=\dfrac{u^2_n+2018u_n-2019}{2020}\Leftrightarrow2020\left(u_{n+1}-1\right)=\left(u_n-1\right)\left(u_n+2019\right)\)
\(\Leftrightarrow\dfrac{2020}{\left(u_n-1\right)\left(u_n+2019\right)}=\dfrac{1}{u_{n+1}-1}\Rightarrow\dfrac{1}{u_n+2019}=\dfrac{1}{u_n-1}-\dfrac{1}{u_{n+1}-1}\left(1\right)\)
Thay n bởi 1 , 2, 3 , ..... , n vào (1) và cộng vế với vế các đẳng thức ta suy ra:
\(S_n=\dfrac{1}{u_1+2019}+\dfrac{1}{u_2+2019}+...+\dfrac{1}{u_n+2019}\)
\(=\dfrac{1}{u_1-1}-\dfrac{1}{u_{n+1}-1}=\dfrac{1}{2018}-\dfrac{1}{u_{n+1}-1}\)
Do \(\left(u_n\right)\) là dãy số tăng nên có 2 trường hợp xảy ra:
th1:
Dãy \(\left(u_n\right)\) bị chặn trên suy ra tồn tại \(lim\) \(u_n\) . Giả sử lim \(u_n\) = x thì \(x\ge2018\)
chuyển qua giới hạn hệ thức \(\left(1\right)khi\) \(n\rightarrow+\infty\) , ta có:
\(x^2+2018x-2020x+1=0\)
\(\Leftrightarrow x^2-2x+1=0\Leftrightarrow x=1\) ( điều này vô lý)
Dãy \(\left(u_n\right)\) ko bị chặn trên , do \(\left(u_n\right)\) tăng và ko bị chặn nên:
\(lim\) \(u_n\)\(=+\infty\Rightarrow lim\left(u_{n+1}-1\right)=+\infty\Rightarrow lim\dfrac{1}{u_{n+1}-1}=0\)
Do vậy: \(limS_n=lim\left(\dfrac{1}{2018}-\dfrac{1}{u_{n+1}-1}\right)=\dfrac{1}{2018}\)
Đúng 2
Bình luận (2)
á cái này bt nek mak gõ hơi chậm nha nói trc cỡ 15p ms xog ó:>
Đúng 1
Bình luận (0)
Bài 1: Xét tính tăng giảm của các dãy số (Un) với
a)\(Un=\dfrac{2^n-1}{2^n+1}\) b)\(Un=\left(-1\right)^n.n\)
Bài 2: Xét tính bị chặn của
\(Un=\sqrt[3]{n}-\sqrt[3]{n+1}\)
mọi người giúp em với ạ , em cảm ơn ạ
cho dãy số (un) thỏa mãn: \(\left\{{}\begin{matrix}u_1=1\\u_{n+1}=\dfrac{n\left(u_n+2\right)+n^2+1}{n+1}\end{matrix}\right.\)
tìm số hạng tổng quát của dãy số
\(u_{n+1}=\dfrac{n\left(u_n+2\right)+n^2+1}{n+1}\)
\(\Rightarrow\left(n+1\right)u_{n+1}=nu_n+n^2+2n+1\)
\(\Rightarrow\left(n+1\right)u_{n+1}-\dfrac{1}{3}\left(n+1\right)^3-\dfrac{1}{2}\left(n+1\right)^2-\dfrac{1}{6}\left(n+1\right)=n.u_n-\dfrac{1}{3}n^3-\dfrac{1}{2}n^2-\dfrac{1}{6}n\)
Đặt \(v_n=u.u_n-\dfrac{1}{3}n^3-\dfrac{1}{2}n^2-\dfrac{1}{6}n\Rightarrow\left\{{}\begin{matrix}v_1=1-\dfrac{1}{3}-\dfrac{1}{2}-\dfrac{1}{6}=0\\v_{n+1}=v_n=...=v_1=0\end{matrix}\right.\)
\(\Rightarrow n.u_n-\dfrac{1}{3}n^3-\dfrac{1}{2}n^2-\dfrac{1}{6}n=0\)
\(\Rightarrow u_n=\dfrac{1}{3}n^2+\dfrac{1}{2}n+\dfrac{1}{6}=\dfrac{\left(n+1\right)\left(2n+1\right)}{6}\)
Đúng 0
Bình luận (0)