Xét tính tăng, giảm của dãy số (un) có số hạng tổng quát un = 2n - 3n
Bài 5: Ôn tập chương Dãy số. Cấp số cộng và cấp số nhân.
Ta sẽ chứng minh dãy này giảm theo quy nạp.
Với n = 1 ta có u1 = -1
Với n = 2 ta có u2 = -5
=> u1 > u2
Giả sử dãy trên đúng với uk > uk+1 tức 2k - 3k > 2(k + 1) - 3k + 1 <=> 2k - 2(k + 1) > 3k - 3k+1
Ta cần chứng minh dãy cũng đúng với uk+1 > uk+2
Hay 2(k + 1) - 3k+1 > 2(k + 2) - 3k+2
<=> 2k - 3.3k > 2(k + 1) - 3.3k+1
<=> 2k - 2(k + 1) > 3.(3k - 3k+1)
Thật vậy: Với k nguyên dương ta luôn có 3k - 3k+1 < 0 và 3 > 1 nên 3(3k - 3k+1) < 3k - 3k+1
Lại có 2k - 2(k + 1) > 3k - 3k+1 => 2k - 2(k + 1) > 3.(3k - 3k+1) (đpcm)
Vậy dãy un trên là dãy giảm
Đúng 0
Bình luận (0)
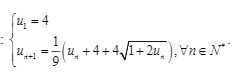 giúp em với mọi người ơi:(
giúp em với mọi người ơi:(
Cho tứ diện ABCD Gọi I,J lần lượt là trọng tâm tam giác ABC,ABD và E,F lần lượt là trung điểm của BC,AC
a/Chứng minh IJ//(ACD)
b/Tìm giao tuyến của và ABD Giúp mk vs mk cần gấp ạ mk cảm ơn
Câu b đề bài thiếu, tìm giao tuyến của mặt nào và (ABD) vậy em?
Đúng 0
Bình luận (0)
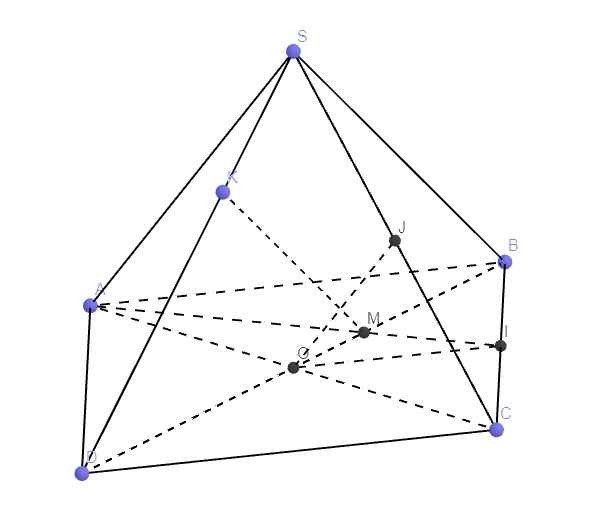
Cho hình chóp S.ABCD có đáy là hình bình hành tâm O. Gọi I, J lần lượt là trung điểm của BC, SC, và K là điểm trên SD sao cho SK = 1/2 KD . a) Chứng minh rằng OJ / /(SAC) và OJ / /(SAB). b) Chứng minh rằng OI / /(SCD) và IJ / /(SBD). c) Gọi M là giao điểm của AI và BD. Chứng minh rằng MK / /(SBC). Cần gấp ạhh
a.
Do O là tâm hbh \(\Rightarrow\) O là trung điểm AC
\(\Rightarrow OJ\) là đường trung bình tam giác SAC
\(\Rightarrow OJ||SA\)
Mà \(SA\in\left(SAC\right)\Rightarrow OJ||\left(SAC\right)\)
\(SA\in\left(SAB\right)\Rightarrow OJ||\left(SAB\right)\)
b. O là trung điểm BD, I là trung điểm BC
\(\Rightarrow OI\) là đườngt rung bình tam giác BCD
\(\Rightarrow OI||CD\)
Mà \(CD\in\left(SCD\right)\Rightarrow OI||\left(SCD\right)\)
Tương tự ta có IJ là đường trung bình tam giác SBC \(\Rightarrow IJ||SB\Rightarrow IJ||\left(SBD\right)\)
c. Ta có I là trung điểm BC, O là trung điểm AC
\(\Rightarrow M\) là trọng tâm tam giác ABC
\(\Rightarrow BM=\dfrac{2}{3}BO=\dfrac{2}{3}.\dfrac{1}{2}BD=\dfrac{1}{3}BD\)
\(\Rightarrow\dfrac{BM}{BD}=\dfrac{1}{3}\)
Theo giả thiết \(SK=\dfrac{1}{2}KD=\dfrac{1}{2}\left(SD-SK\right)\Rightarrow SK=\dfrac{1}{3}SD\)
\(\Rightarrow\dfrac{SK}{SD}=\dfrac{1}{3}=\dfrac{BM}{BD}\Rightarrow KM||SB\) (Talet đảo)
\(\Rightarrow MK||\left(SBC\right)\)
Đúng 0
Bình luận (0)
cho cấp số cộng (Un) có công sai d= -2 và Sn =72.Tính U1
Đề bài sai, không thể tính \(u_1\) (sẽ có vô số giá trị \(u_1\) thỏa mãn)
Đúng 0
Bình luận (0)
Có 3 cây bút chì màu đỏ .8 cây bút chì màu xanh .lấy ngẫu nhiên 5 cây bút chì .Tính xác suất để lấy ra 2 bút chì màu đỏ và 3 bút chì màu xanh
Không gian mẫu: \(C_{11}^5=462\)
Số cách lấy ra 2 bút đỏ, 3 bút xanh: \(C_3^2.C_8^3=168\)
Xác suất: \(P=\dfrac{168}{462}=\dfrac{4}{11}\)
Đúng 0
Bình luận (0)
S=2838 \(C^0_8\) + 2737 \(C^1_8\) +...+ \(C^8_8\)
S= 2n \(C^0_n\)+ 2n-2 \(C^{n-2}_n\) + 2n-4 \(C^{n-4}_n\) +...+\(C^n_n\)
giúp em với ạ
a.
Xét khai triển:
\(\left(1+x\right)^8=C_8^0x^8+C_8^1x^7+...+C_8^7x+C_8^8\)
Thay \(x=2.3=6\) ta được:
\(\left(1+6\right)^8=C_8^0.2^83^8+C_8^12^73^7+...+C_8^8\)
\(\Rightarrow S=7^8\)
b.
Câu này quy luật tổng S không đúng (nó ko hợp lý ở số hạng cuối \(C_n^n\), số hạng cuối là \(C_n^n\) chỉ khi n là số chẵn, còn n là số lẻ thì số hạng cuối phải là \(2^1.C_n^{n-1}\))
Coi như n là số chẵn:
Do \(C_n^k=C_n^{n-k}\) nên ta có thể viết lại cho quy luật dễ nhìn hơn:
\(S=2^nC_n^0+2^{n-2}C_n^2+2^{n-4}C_n^4+...+C_n^n\)
Xét khai triển:
\(\left(1+x\right)^n=C_n^0x^n+C_n^1x^{n-1}+C_n^2x^{n-2}+...+C_n^{n-2}x^2+C_n^{n-1}x+C_n^n\) (1)
Xét khai triển
\(\left(1-x\right)^n=C_n^0.\left(-x\right)^n+C_n^1\left(-x\right)^{n-1}+C_n^2.\left(-x\right)^{n-2}+...+C_n^{n-2}\left(-x\right)^2+C_n^{n-1}\left(-x\right)+C_n^n\)
Do n chẵn
\(\Rightarrow\left(1-x\right)^n=C_n^0x^n-C_n^1x^{n-1}+C_n^{n-2}x^{n-2}+...+C_n^n\) (2)
Cộng vế (1) và (2):
\(\Rightarrow\left(1+x\right)^n+\left(1-x\right)^n=2\left[C_n^0x^n+C_n^2x^{n-2}+...+C_n^n\right]\)
\(\Rightarrow C_n^0x^n+C_n^2x^{n-2}+...+C_n^n=\dfrac{\left(1+x\right)^n+\left(1-x\right)^n}{2}\)
Thay \(x=2\)
\(\Rightarrow C_n^0.2^n+C_n^22^{n-2}+...+C_n^n=\dfrac{3^n+1}{2}\)
\(\Rightarrow S=\dfrac{3^n+1}{2}\)
Đúng 0
Bình luận (0)
s=2^(n)*c_(n)^(0)+2^(n-2)*c_(n)^(n-2)+2^(n-4)*c_(n)^(n-4)+...+c_(n)^(n)
giúp em với ạ
Đề thế này thì không thể hiểu được.
Em sử dụng công cụ soạn thảo toán học để đăng lại đề nhé, nó ở đây:

Mũ thì bấm "^" là được
Còn kí hiêu tổ hợp kiểu \(C_n^k\) thì ở đây:
Sau đó chọn
Hoặc đơn giản hơn thì vào chỗ gõ công thức (biểu tượng tổng sigma nói ở trên), sau đó bấm C, rồi shift _, bấm tiếp mũi tên sang phải ở bàn phím, rồi shift ^, tiếp tục mũi tên sang phâir
Đúng 0
Bình luận (0)
S= 2nC0n + 2n-2 Cn-2n +2n-4 Cnn-4 +...+Cnn
Đúng 0
Bình luận (0)
Giúp em với ạ!
Đọc tiếp
Giúp em với ạ!
Ta dễ dàng quy nạp dãy \(u_n\) là dãy dương
Từ đó: \(u_n-u_{n-1}=u_{n-1}^2+u_{n-1}>0\Rightarrow\) dãy tăng
\(u_n+1=\left(u_{n-1}+1\right)^2\)
Đặt \(u_n+1=v_n\Rightarrow v_1=u_1+1=2\)
\(v_n=v_{n-1}^2=v_{n-2}^{2^2}=v_{n-3}^{2^3}=...=v_1^{2^{n-1}}=2^{2^{n-1}}\)
\(\Rightarrow u_n=v_n-1=2^{2^{n-1}}-1\)
Đúng 1
Bình luận (1)
\(u_1=1>0\)
\(u_2=u_1^2+2u_1=3>0\)
Giả sử \(u_k>0\) , ta cần chứng minh \(u_{k+1}>0\)
Hiển nhiên có \(u_{k+1}=u_k^2+2u_k>0^2+2.0=0\)
Đúng 1
Bình luận (0)
cho dãy số un xác định bởi \(\left\{{}\begin{matrix}u1=2\\u_{n+1}=un+3\end{matrix}\right.\)với n\(\ge1\) Tính I=lim \(\dfrac{un}{3n+1}\)
Từ công thức dãy số ta thấy \(u_n\) là cấp số cộng với \(\left\{{}\begin{matrix}u_1=2\\d=3\end{matrix}\right.\)
\(\Rightarrow u_n=u_1+\left(n-1\right)d=2+\left(n-1\right)3=3n-1\)
\(\Rightarrow I=\lim\limits\dfrac{3n-1}{3n+1}=1\)
Đúng 1
Bình luận (0)