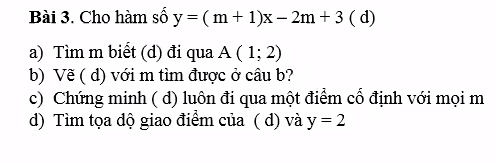
Bài 5: Hệ số góc của đường thẳng y = ax + b ( a khác 0)

mình làm câu dưới r nha

Thay y = 1 vào đường thẳng y = 2x - 4 ta có:

2x - 4 = 1

2x = 1 + 4

2x = 5

x = 5/2

Thay x = 5/2 và y = 1 vào đường thẳng y = 5x - 2m + 4 ta có:

5.5/2 - 2m + 4 = 1

25/2 - 2m + 4 = 1

33/2 - 2m = 1

2m = 33/2 - 1

2m = 31/2

m = 31/4

Vậy m = 31/4 thì hai đường thẳng đã cho cắt nhau tại điểm có tung độ bằng 1

a:

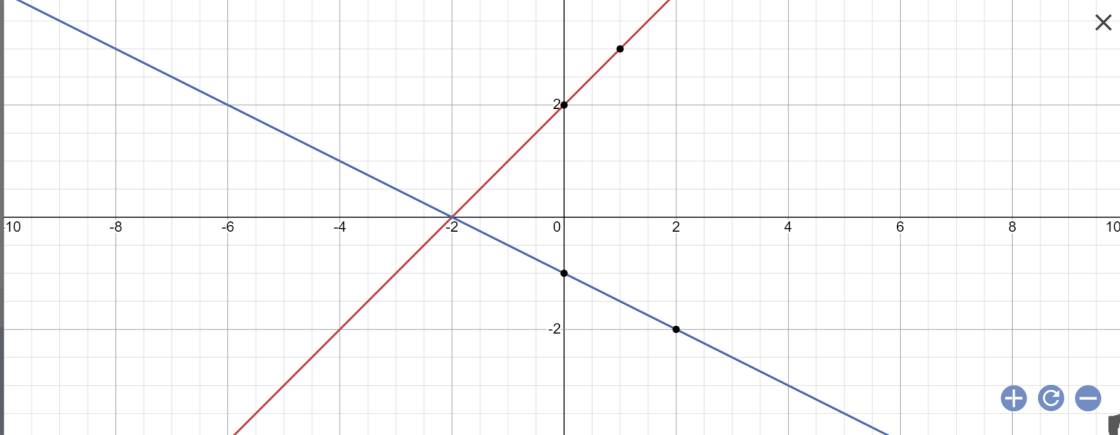
Phương trình hoành độ giao điểm là:

\(x+2=-\dfrac{1}{2}x-1\)

=>\(x+\dfrac{1}{2}x=-1-2\)

=>1,5x=-3

=>x=-3/1,5=-2

Thay x=-2 vào y=x+2, ta được:

y=-2+2=0

Vậy: (d1) cắt (d2) tại điểm A(-2;0) nằm trên trục hoành

b: Tọa độ B là:

\(\left\{{}\begin{matrix}x=0\\y=x+2=0+2=2\end{matrix}\right.\)

Tọa độ C là:

\(\left\{{}\begin{matrix}x=0\\y=-\dfrac{1}{2}x-1=-\dfrac{1}{2}\cdot0-1=-1\end{matrix}\right.\)

A(-2;0); B(0;2); C(0;-1)

\(AB=\sqrt{\left(0+2\right)^2+\left(2-0\right)^2}=2\sqrt{2}\)

\(AC=\sqrt{\left(0+2\right)^2+\left(-1-0\right)^2}=\sqrt{2^2+\left(-1\right)^2}=\sqrt{5}\)

\(BC=\sqrt{\left(0-0\right)^2+\left(-1-2\right)^2}=\sqrt{0^2+\left(-3\right)^2}=3\)

Xet ΔABC có \(AB^2+AC^2=BC^2\)

nên ΔABC vuông tại A

=>\(\widehat{BAC}=90^0\)

Xét ΔABC vuông tại A có \(sinB=\dfrac{AC}{BC}=\dfrac{\sqrt{5}}{3}\)

nên \(\widehat{B}\simeq48^011'\)

Ta có: ΔABC vuông tại A

=>\(\widehat{ABC}+\widehat{ACB}=90^0\)

=>\(\widehat{ACB}+48^011'=90^0\)

=>\(\widehat{ACB}=41^049'\)

c: Chu vi tam giác ABC là:

\(C_{ABC}=AB+AC+BC=2\sqrt{2}+\sqrt{5}+3\)

Vì ΔABC vuông tại A

nên \(S_{ABC}=\dfrac{1}{2}\cdot AB\cdot AC=\dfrac{1}{2}\cdot2\sqrt{2}\cdot\sqrt{5}=\sqrt{10}\)

Lời giải:

$A$ thuộc trục tung nên $x_A=0$

$y_A=2x_A+m+5=2.0+m+5=m+5$. Vậy $A(0,m+5)$

$B$ thuộc trục hoành nên $y_B=0$

$0=y_B=2x_B+m+5$

$\Rightarrow x_B=\frac{-m-5}{2}$

Vậy $B(\frac{-m-5}{2},0)$
\(AB=\sqrt{(x_A-x_B)^2+(y_A-y_B)^2}=\sqrt{5}\)

$\Leftrightarrow (x_A-x_B)^2+(y_A-y_B)^2=5$

$\Leftrightarrow (0-\frac{-m-5}{2})^2+(m+5-0)^2=5$

$\Leftrightarrow \frac{(m+5)^2}{4}+(m+5)^2=5$

$\Leftrightarrow (m+5)^2=4\Leftrightarrow m+5=\pm 2$

$\Rightarrow m=-3$ hoặc $m=-7$

Lời giải:

$(d)$ cắt trục tung tại điểm có tung độ bằng -1, tức là $(d)$ cắt trục tung tại điểm $(0,-1)$

$\Rightarrow -1=(2m-1).0-3m+5$

$\Leftrightarrow -1=-3m+5\Leftrightarrow -6=-3m$

$\Leftrightarrow m=2$

Với $m=2$ thì đths là $y=3x-1$ (bạn có thể tự vẽ)

c.

Giả sử $(d)$ luôn đi qua 1 điểm cố định với mọi $m$ như đề nói. Gọi điểm đó là $(x_0,y_0)$.

Khi đó:
$y_0=(2m-1)x_0-3m+5, \forall m$

$\Leftrightarrow 2mx_0-x_0-3m+5-y_0=0, \forall m$

$\Leftrightarrow m(2x_0-3)+(5-x_0-y_0)=0, \forall m$

$\Rightarrow 2x_0-3=5-x_0-y_0=0$
$\Leftrightarrow x_0=\frac{3}{2}; y_0=\frac{7}{2}$
Vậy $(d)$ luôn đi qua điểm cố định $(\frac{3}{2}; \frac{7}{2})$

a: Vì (d)//y=1/2x+1 nên \(\left\{{}\begin{matrix}a=\dfrac{1}{2}\\b\ne1\end{matrix}\right.\)

Vậy: (d): \(y=\dfrac{1}{2}x+b\)

Thay x=2 và y=2 vào (d), ta được:

\(b+\dfrac{1}{2}\cdot2=2\)

=>b+1=2

=>b=1

vậy: (d): \(y=\dfrac{1}{2}x+1\)

b: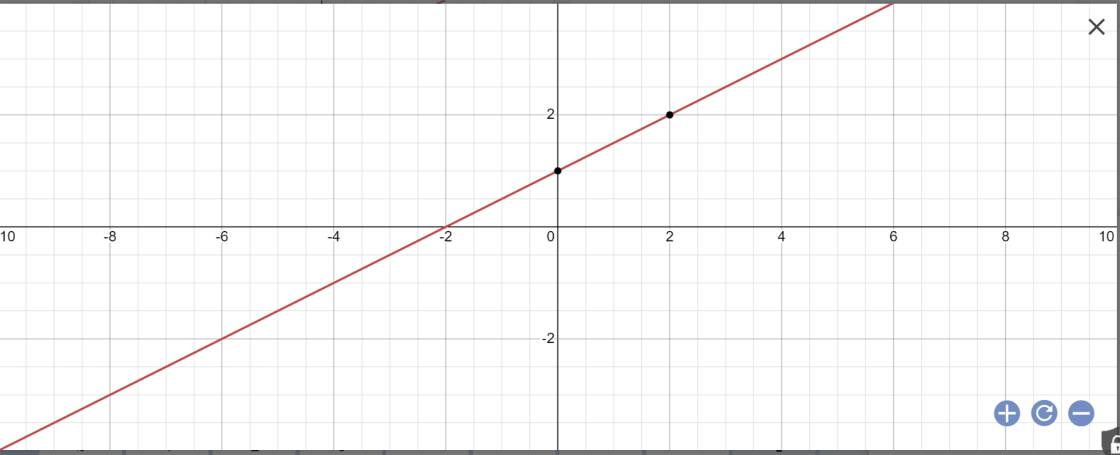 

c: Gọi \(\alpha\) là góc tạo bởi (d) với trục Ox

Ta có: (d): \(y=\dfrac{1}{2}x+1\)

=>a=1/2

=>\(tan\alpha=a=\dfrac{1}{2}\)

=>\(\alpha\simeq26^034'\)

d: tọa độ B là:

\(\left\{{}\begin{matrix}y=0\\\dfrac{1}{2}x+1=0\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}y=0\\\dfrac{1}{2}x=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=0\\x=-2\end{matrix}\right.\)

Tọa độ C là;

\(\left\{{}\begin{matrix}x=0\\y=\dfrac{1}{2}x+1=\dfrac{1}{2}\cdot0+1=1\end{matrix}\right.\)

Vậy: B(-2;0); C(1;0)

\(OB=\sqrt{\left(-2-0\right)^2+\left(0-0\right)^2}=\sqrt{2^2+0^2}=2\)

\(OC=\sqrt{\left(1-0\right)^2+\left(0-0\right)^2}=\sqrt{1^2+0^2}=1\)

Vì Ox\(\perp\)Oy nên OB\(\perp\)OC

=>ΔBOC vuông tại O

=>\(S_{BOC}=\dfrac{1}{2}\cdot OB\cdot OC=\dfrac{1}{2}\cdot2\cdot1=1\)

a: Thay x=1 và y=0 vào (d), ta được:

\(1\left(3-2m\right)+m-1=0\)

=>3-2m+m-1=0

=>2-m=0

=>m=2

b: Thay x=0 và y=-4 vào (d), ta được:

\(0\cdot\left(3-2m\right)+m-1=-4\)

=>m-1=-4

=>m=-4+1=-3

c: Thay x=3 và y=3 vào (d), ta được:

\(3\left(3-2m\right)+m-1=3\)

=>9-6m+m-1=3

=>8-5m=3

=>5m=8-3=5

=>m=1

Thay x=1 và y=6 vào (d), ta được:

\(1\left(m-2\right)+3=6\)

=>m-2=3

=>m=5

Khi m=5 thì (d): \(y=\left(5-2\right)x+3=3x+3\)

(d): y=3x+3 và (d1): y=3x-1

Vì \(\left\{{}\begin{matrix}a=a'\left(3=3\right)\\b< >b'\left(3< >-1\right)\end{matrix}\right.\)

nên (d)//(d1)

Sửa đề: ΔABC cân tại A

a: Sửa đề: AB là trung bình nhân của AE và AH

CF//BH

CF\(\perp\)AB

Do đó: BA\(\perp\)BH

=>ΔBAH vuông tại B

Xét ΔBAH vuông tại B có BE là đường cao

nên \(AE\cdot AH=AB^2\)

=>\(AB=\sqrt{AE\cdot AH}\)

=>AB là trung bình nhân của AE và AH

b: Từ C, kẻ CG\(\perp\)CB, \(G\in AB\)

ΔABC cân tại A

mà AD là đường cao

nên D là trung điểm của BC

Xét ΔBCG có

D là trung điểm của BC

DA//CG

Do đó: A là trung điểm của BG

Xét ΔBCG có D,A lần lượt là trung điểm của BC,BG

=>DA là đường trung bình

=>CG=2DA

=>4DA^2=CG^2

Xét ΔCBG vuông tại C có CF là đường cao

nên \(\dfrac{1}{CF^2}=\dfrac{1}{CG^2}+\dfrac{1}{CB^2}\)

=>\(\dfrac{1}{CF^2}=\dfrac{1}{4DA^2}+\dfrac{1}{CB^2}\)

Gọi đường thẳng cần tìm là `y=ax+b`   `(1)`

`a)` Thay `A(4;0);B(-1;2)` vào `(1)` có hệ:

   `{(4a+b=0),(-a+b=2):}<=>{(a=2/5),(b=-8/5):}`

 `=>` Ptr đường thẳng `(1)` là: `y=2/5x-8/5`

`b)-2x+y=3<=>y=2x-3`

`(1) \bot y=2x-3<=>a.2=-1<=>a=-1/2`

Thay `a=-1/2; M(-1;2)` vào `(1)` có:

      `2=-1/2 .(-1)+b<=>b=3/2`

  `=>` Ptr đường thẳng `(1)` là: `y=-1/2x+3/2`.