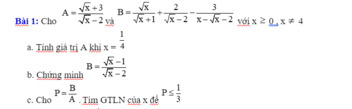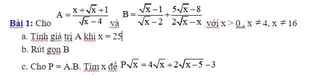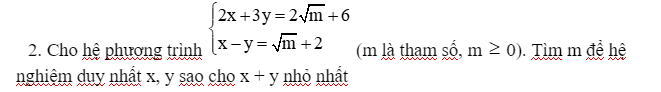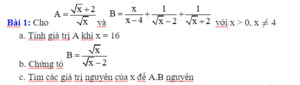BÀI 1. Giải các phương trình sau bằng công thức nghiệm hoặc (công thức nghiện thu gọn). 1) x2 - 11x + 38 = 0 ; 2) 6x2 + 71x + 175 = 0 ; 3) 5x2 - 6x + 27 = 0 ; 4) - 30x2 + 30x - 7,5 = 0 ; 5) 4x2 - 16x + 17 = 0 ; 6) x2 + 4x - 12 = 0 ;
Bài 5: Công thức nghiệm thu gọn
1, \(\Delta=\left(-11\right)^2-4.1.38=121-152=-31< 0\)
\(\Rightarrow\) pt vô nghiệm
2, \(\Delta=71^2-4.6.175=5041-4200=841\)
\(x_1=\dfrac{-71+\sqrt{841}}{2.6}=\dfrac{-71+29}{12}=\dfrac{-42}{12}=-\dfrac{7}{2}\)
\(x_2=\dfrac{-71-\sqrt{841}}{2.6}=\dfrac{-71-29}{12}=\dfrac{-10}{12}=-\dfrac{25}{3}\)
3, \(\Delta=\left(-3\right)^2-5.27=9-135=-126< 0\)
⇒ pt vô nghiệm
4, \(\Delta=15^2-\left(-30\right)\left(-7,5\right)=225-225=0\)
\(\Rightarrow x_1=x_2=\dfrac{-30}{2.\left(-30\right)}=\dfrac{1}{2}\)
5, \(\Delta'=\left(-8\right)^2-4.17=64-68=-4\)
⇒ pt vô nghiệm
6, \(\Delta=4^2-4.1.\left(-12\right)=16+48=64\)
\(x_1=\dfrac{-4+\sqrt{64}}{2.1}=\dfrac{-4+8}{2}=\dfrac{4}{2}=2\)
\(x_2=\dfrac{-4-\sqrt{64}}{2.1}=\dfrac{-4-8}{2}=\dfrac{-12}{2}=-6\)
Đúng 1
Bình luận (1)
a; Thay x=1/4 vào A, ta được:
\(A=\left(\dfrac{1}{2}+3\right):\left(\dfrac{1}{2}-2\right)=\dfrac{7}{2}:\dfrac{-3}{2}=\dfrac{-7}{3}\)
b: \(B=\dfrac{x-2\sqrt{x}+2\sqrt{x}+2-3}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-2\right)}=\dfrac{\sqrt{x}-1}{\sqrt{x}-2}\)
Đúng 3
Bình luận (0)
x + y = -10
x - y = \(\dfrac{288}{41}\)
Hỏi: x=? , y=?
\(\left\{{}\begin{matrix}x+y=-10\\x-y=\dfrac{288}{41}\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x+y=-10\\2x=\dfrac{-122}{41}\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}\dfrac{-61}{41}+y=-10\\x=\dfrac{-61}{41}\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}y=\dfrac{-349}{41}\\x=\dfrac{-61}{41}\end{matrix}\right.\)
Đúng 8
Bình luận (0)
a: Thay x=25 vào A, ta được:
\(A=\dfrac{25+5+1}{5-4}=31\)
b: \(B=\dfrac{x-\sqrt{x}-5\sqrt{x}+8}{\sqrt{x}\left(\sqrt{x}-2\right)}=\dfrac{\sqrt{x}-4}{\sqrt{x}}\)
Đúng 0
Bình luận (0)
a, \(A=\dfrac{\sqrt{x}+2}{\sqrt{x}}=\dfrac{\sqrt{16}+2}{\sqrt{16}}=\dfrac{4+2}{4}=\dfrac{6}{4}=\dfrac{3}{2}\)
b, \(B=\dfrac{x}{x-4}+\dfrac{1}{\sqrt{x}-2}+\dfrac{1}{\sqrt{x}+2}\)
\(\Rightarrow B=\dfrac{x}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}+\dfrac{\sqrt{x}+2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}+\dfrac{\sqrt{x}-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\)
\(\Rightarrow B=\dfrac{x+\sqrt{x}+2+\sqrt{x}-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\)
\(\Rightarrow B=\dfrac{x+2\sqrt{x}}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\)
\(\Rightarrow B=\dfrac{\sqrt{x}\left(\sqrt{x}+2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\)
\(\Rightarrow B=\dfrac{\sqrt{x}}{\sqrt{x}-2}\)
c,\(AB=\dfrac{\sqrt{x}+2}{\sqrt{x}}.\dfrac{\sqrt{x}}{\sqrt{x}-2}\)
\(\Rightarrow AB=\dfrac{\sqrt{x}+2}{\sqrt{x}-2}\)
\(\Rightarrow AB=\dfrac{\sqrt{x}-2+4}{\sqrt{x}-2}\)
\(\Rightarrow AB=1+\dfrac{4}{\sqrt{x}-2}\)
Để AB nguyên thì \(\dfrac{4}{\sqrt{x}-2}\in Z\Rightarrow\sqrt{x}-2\inƯ\left(4\right)\)
Ta có bảng:
| \(\sqrt{x}-2\) | -4 | -2 | -1 | 1 | 2 | 4 |
| x | vô lí | 0 (ktm) | 1 | 9 | 16 | 36 |
Vậy \(x\in\left\{1;9;16;36\right\}\)
Đúng 7
Bình luận (2)
a, B=xx−4+1√x−2+1√x+2B=xx−4+1x−2+1x+2
⇒B=x+√x+2+√x−2(√x−2)(√x+2)⇒B=x+x+2+x−2(x−2)(x+2)
⇒B=√x(√x+2)(√x−2)(√x+2)⇒B=x(x+2)(x−2)(x+2)
AB=√x+2√x.√x√x−2AB=x+2x.xx−2
⇒AB=√x−2+4√x−2⇒AB=x−2+4x−2
4√x−2∈Z⇒√x−2∈Ư(4)4x−2∈Z⇒x−2∈Ư(4)
Ta có bảng:
| √x−2x−2 | -4 | -2 | -1 | 1 | 2 | 4 |
| x | vô lí | 0 (ktm) | 1 | 9 | 16 | 36 |
Vậy x∈{1;9;16;36}
Đúng 1
Bình luận (0)
phân tích đa thức thành nhân tử:
(b2 + c2 - a2 )2 - 4b2c2
\(=\left(b^2+c^2+2bc-a^2\right)\left(b^2+c^2-2bc-a^2\right)\)
\(=\left(b+c-a\right)\left(b+c+a\right)\left(b-c-a\right)\left(b-c+a\right)\)
Đúng 1
Bình luận (0)
Cho phương trình \(mx^2-2\left(m-1\right)x+m-3=0\)
Giải và biện luận phương trình trên.
Với \(m=0\)
\(PT\Leftrightarrow2x-3=0\Leftrightarrow x=\dfrac{3}{2}\)
Với \(m\ne0\)
\(\Delta'=\left(m-1\right)^2-m\left(m-3\right)=m+1\)
PT vô nghiệm \(\Leftrightarrow m+1< 0\Leftrightarrow m< -1\)
PT có nghiệm kép \(\Leftrightarrow m+1=0\Leftrightarrow m=-1\)
\(\Leftrightarrow x=-\dfrac{b'}{a}=\dfrac{m-1}{2m}\)
PT có 2 nghiệm phân biệt \(\Leftrightarrow m+1>0\Leftrightarrow m>-1;m\ne0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{m-1+\sqrt{m+1}}{m}\\x=\dfrac{m-1-\sqrt{m+1}}{m}\end{matrix}\right.\)
Đúng 1
Bình luận (0)
4.
Phương trình đã cho có 2 nghiệm pb khi:
\(\Delta'=\left(m+1\right)^2-\left(m^2+2\right)>0\)
\(\Leftrightarrow2m-1>0\)
\(\Leftrightarrow m>\dfrac{1}{2}\)
5.
Pt đã cho vô nghiệm khi:
\(\Delta'=9-3\left(3k+1\right)< 0\)
\(\Leftrightarrow9k>6\)
\(\Rightarrow k>\dfrac{2}{3}\)
Đúng 2
Bình luận (0)
\(\dfrac{1}{2x-1}+2x=0\)
giải phương trình
ĐKXĐ \(x\ne\dfrac{1}{2}\)
\(\Leftrightarrow\dfrac{1}{2x-1}+\dfrac{2x\left(2x-1\right)}{2x-1}=0\)
\(\Rightarrow1+2x\left(2x-1\right)=0\)
\(\Leftrightarrow4x^2-2x+1=0\)
\(\Leftrightarrow\left(2x-\dfrac{1}{2}\right)^2+\dfrac{3}{4}=0\)
Do \(\left(2x-\dfrac{1}{2}\right)^2\ge0\Rightarrow\left(2x-\dfrac{1}{2}\right)^2+\dfrac{3}{4}>0;\forall x\)
Pt đã cho vô nghiệm
Đúng 2
Bình luận (0)